OO 第一单元总结
OO第一单元总结
代码架构设计
第一单元总共有三次作业,从第一次简单的单变量拆括号,到第二次引入了自定义函数和三角函数,再到第三次作业去掉了对于函数嵌套和三角函数的种种限制,本质上是在不断地实现同一类问题的更复杂的需求。由于OO每次只发布当前作业的要求,不透露以后的需求,这就要求我们每次作业的架构要有一定的可扩展性,否则只能含泪重构。下面我将介绍我三次作业的架构,并附上个人对于架构设计的一些心得。
对于整个第一单元的设计,我认为有两个部分至关重要——表达式的存储和表达式的解析。所谓表达式的存储,就是如何用数据结构来存储一个表达式使其能够方便地进行所需操作;而表达式的解析,就是如何将读入的字符串中的信息存到设计好的数据结构中。我的整个设计思路都是围绕着这两部分,也将在下文着重介绍这两部分。
第一次作业
下面是第一次作业的UML类图。可以看到结构比较简单,一共只有五个类,其中Term类和Expr类用来实现表达式的存储,Parser类和Lexer类用来实现表达式的解析,Main类负责统一调配。
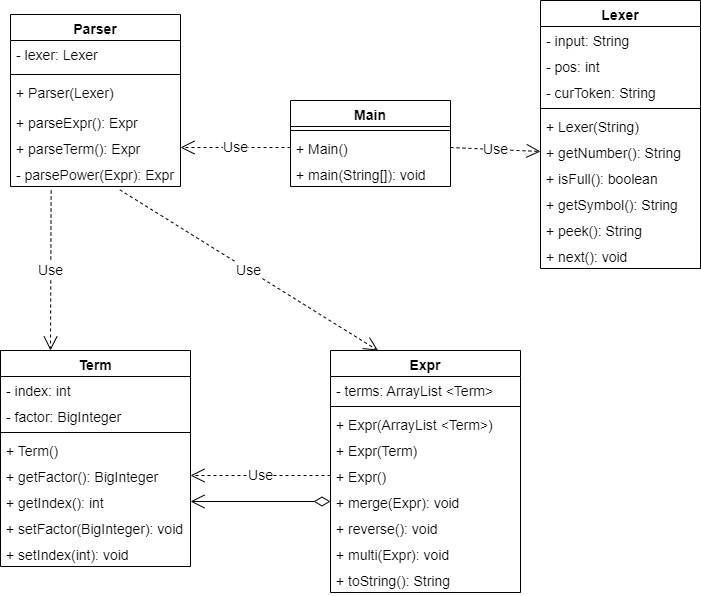
在表达式的存储上,我只设计了Expr和Term两级结构,其中Term代表由乘号相连接的一项,Expr代表由加/减号相连接的项组成的表达式。之所以没有像其他同学那样设计一个单独的Factor类用来表示x和常数,是因为第一次作业Factor过于简单,可以直接合并到Term之中。当然,这里欠的债是要在第二次作业里还的(doge)。这一部分比较重要的是Expr的multi方法和merge方法,用来支持表达式之间的乘法和合并同类项。这告诉我们一个道理:一个好的数据结构应该既能巧妙地保存数据(属性),又能方便地操作数据(方法)。数据结构的设计是程序设计的根本,要为复杂的上层设计提供良好的工具箱。
另一方面,在表达式的解析上,我沿袭了train1的思路,改写了Parser类和Lexer类。由于第一次作业数据会有连续的符号出现,我在Lexer类中补充了getSymbol方法,把连续的符号变成一个。Parser类的实现十分复杂,究其原因,一来是本身算式就比较复杂,需要判断很多情况;二来是Parser类解析时需要递归操作,但是Lexer类是从左到右遍历的,并不是一个良好的递归结构,因此在递归上常常出错,也是本次作业中我debug最久的部分。
如果仔细观察会发现一个奇怪的现象:parseExpr方法和parseTerm方法返回的都是Expr类型。这其实是无奈之举。因为Term是根据乘号递归运算的,即 2 * x * 3 的实际执行顺序是 2 * (x * 3),而如果遇到 2 * (x + 1) 这种情况,返回值就必须是Expr。这暴露了一个问题:类的设计上缺乏清晰的界限。如果Expr和Term在某些场景会混为一谈,说明类的设计并不具备清晰的结构,即没有达到设计上的逻辑自洽。其实解决方法也比较简单,参考train2的设计,让Expr和Term都继承一个接口,都作为一种因子看待。
总的来说,在第一次作业中,我实现了基本的数据结构框架,也确定了解析的方式。之后两次作业的设计,虽然相较第一次改了很多,但都没有超出这个框架。还保留了Expr、Term的结构,还是Parser+Lexer的解析方式。
第二次作业
第二次作业相比第一次作业多了自定义函数和三角函数,难度陡增。针对这两个问题,我新增了两个类,Func类和Factor类。以下是第二次作业的UML类图。
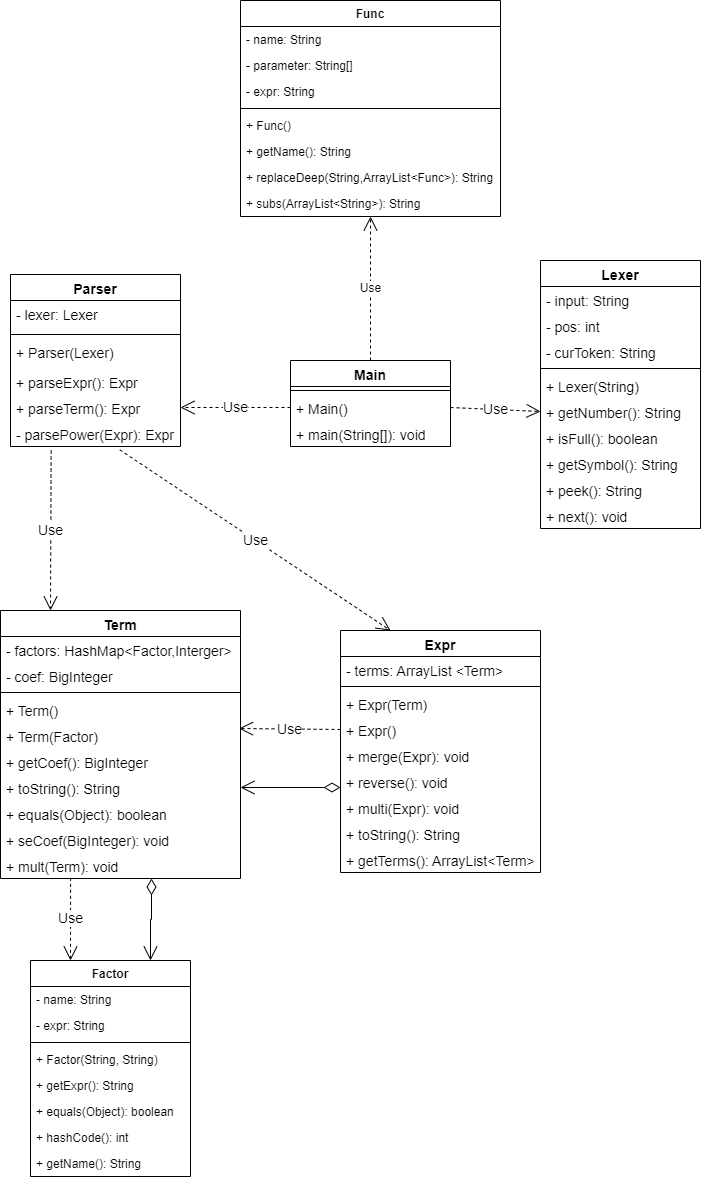
在表达式的存储上,新增了Factor类。这一次为了可扩展性,我直接用name和expr来表示因子,这样不管是新增函数还是其他的自变量都可以解决。值得注意的是Factor的属性expr的类型是String而非Expr,这其实是由于equals方法和hashCode方法实现的时候有些bug,临时改用String类型替代。当然,由于第二次作业中三角函数里面只能是幂函数或常数,并不影响正确性和性能,在第三次作业中已经改成了Expr类型。
另一个重要变化是Term的结构。由于增加了三角函数,不能用简单的系数+指数的方式存储一项的数据了,而是改用Hashmap存储每一种因子和其对应的指数,再用BigInteger记录这一项的系数。这种结构在合并同类项的时候非常方便,而且还有一个意想不到的好处——任何因子的0次方都是1。
最让人纠结的部分在表达式的解析上。因为新增加了自定义函数,使表达式的结构完全变了。当时的我有两个选择:
- 把自定义函数的代换作为读入的预处理,通过一个独立的类用replace方法暴力解决
- 把自定义函数作为解析的一部分,重构Parser的功能,实现自定义函数的代换
尽管助教学长极力推荐后者,我还是毅然决然地选择了前者。因为当时我还没有增加Factor类,对于多变量的解析一头雾水。而且没有考虑暴力替换可能带来的bug,感觉实现比较简单,幸而最后在大家的帮助下搞定了所有的bug。
预处理的功能主要有Func类的静态方法replaceDeep实现。首先,从左到右遍历输入的字符串,如果检测到了自定义函数名,就用计数器做括号匹配(左括号计数器+1,右括号计数器-1),如果计数器的值为1且读到了',',就把','之前字符串的放入参数列表,先对参数列表中的参数递归处理,再用subs方法带入自定义函数的表达式。这其中踩了不少坑,在后边bug分析部分会讲。
此时此刻,当我坐在这里复盘整个作业的时候,并没有为选择第一种方法而后悔。诚然,它不够优雅,要趟过不少坑,也不像解析法那样具有极高的可扩展性。但是它却具有很多优点:
- 完全符合开闭原则,预处理的过程与之后的化简过程完全分开,方便调试
- 实现很简洁,整个Func类只有80行
- 具有一定的可扩展性,只要函数名和变量名已知,就可以满足需求
完成这个功能我前后只花了两天,挺过了两次强测和Hack,我认为它可以被称为合格的设计。引用一下强哥的观点:“架构设计本无高低优劣之分”。何为优雅?实用即可。
第三次作业
由于该设计的都设计完了,第三次作业基本上没什么改动,唯一的改变就是增加了一个三角优化:
具体的思路就是枚举任意两个Term,去掉它们的公共项之后比较剩余的项是否满足以上公式的格式,若满足,则可以合并。这个优化的代价就是程序运行速度会变得很慢,毕竟枚举的复杂度太高了,不过强测的时限挺长,数据也没有很极端。
圈复杂度分析
圈复杂度是一种度量代码复杂度的方法,当程序中出现分支或循环语句时,代码的圈复杂度将会增加。圈复杂度越高,代码的可读性越差,相应的越可能出现bug。下面我将分析我代码的圈复杂度。
首先查看各个类的平均圈复杂度,发现其中Expr类、Func类、Parser类的圈复杂度较高。让我们逐一查看这些类各个方法的圈复杂度,来寻找圈复杂度高的原因。
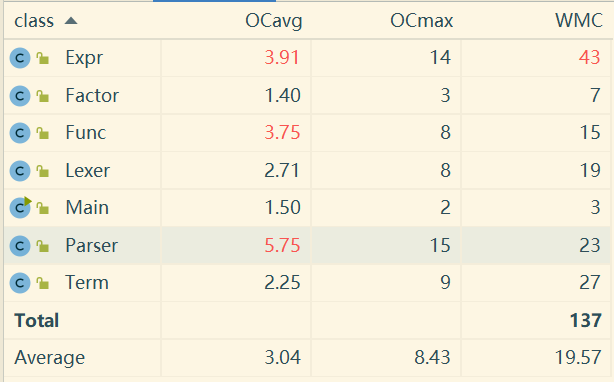
Expr
Expr类中的方法圈复杂度大多比较正常,只有simplify方法一枝独秀,simplify方法是用来完成三角优化的方法,对于每次合并完的Expr都会调用simplify进行三角优化。
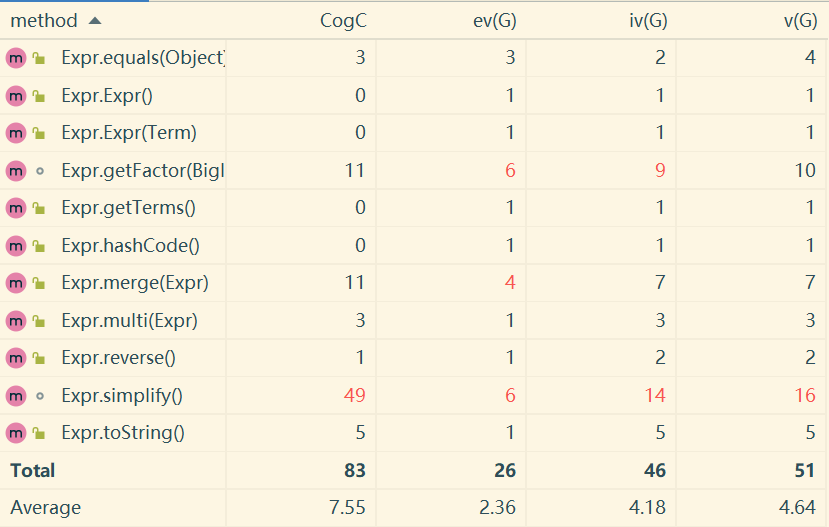
simplify方法之所以圈复杂度如此之高,是因为枚举Term和Term中因子的时候使用了多重循环,加之判断三角优化的条件十分复杂,导致循环中的分支判断也有很多,所以圈复杂度相当高。在实现这个方法之后,我也思考过对其进行优化和扩展。方法是将三角优化的判断单独作为一个私有方法来处理,这样不仅能够有效降低代码圈复杂度,还能具备良好的扩展性,进而实现更多的三角优化。不过受限于时间,我尚未实现。
void simplify() {
while (true) {
boolean isMerged = false;
for (int i = 0;i < terms.size(); i++) {
Term term1 = terms.get(i);
for (int j = 0;j < terms.size(); j++) {
Term term2 = terms.get(j);
BigInteger conFactor = getFactor(term1.getCoef(),term2.getCoef());
if (conFactor == null) {
continue;
}
HashMap<Factor,Integer> s = new HashMap<>();
HashMap<Factor,Integer> t1 = new HashMap<>();
HashMap<Factor,Integer> t2 = new HashMap<>();
HashMap<Factor,Integer> factors1 = term1.getFactors();
HashMap<Factor,Integer> factors2 = term2.getFactors();
for (Factor factor : factors1.keySet()) {
if (!factors2.containsKey(factor)) {
t1.put(factor,factors1.get(factor));
} else if (factors1.get(factor) <= factors2.get(factor)) {
s.put(factor,factors1.get(factor));
t2.put(factor,factors2.get(factor) - factors1.get(factor));
} else {
s.put(factor,factors2.get(factor));
t2.put(factor,factors1.get(factor) - factors2.get(factor));
}
}
for (Factor factor : factors2.keySet()) {
if (!factors1.containsKey(factor)) {
t2.put(factor,factors2.get(factor));
}
}
if (t1.size() == 1 && t2.size() == 1) {
Factor factor1 = t1.keySet().iterator().next();
Factor factor2 = t2.keySet().iterator().next();
if (factor1.getExpr().equals(factor2.getExpr())) {
if (t1.get(factor1) == 2 && t2.get(factor2) == 2) {
isMerged = true;
term1.setCoef(term1.getCoef().add(conFactor.negate()));
term2.setCoef(term2.getCoef().add(conFactor.negate()));
terms.add(new Term(s,conFactor));
}
}
}
}
}
if (!isMerged) {
break;
}
}
}
Func
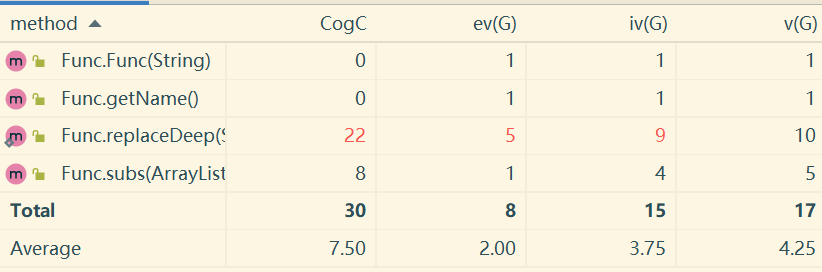
Func类主要的圈复杂度问题在于replaceDeep方法。由于replaceDeep方法是直接对字符串进行解析,所以分支判断很多,造成了圈复杂度较高。由于replaceDeep方法需要递归调用,所以难以像simplify那样拆分函数,所幸replaceDeep方法并不冗长,只有30行,还是具备较好的可读性的。
Parser
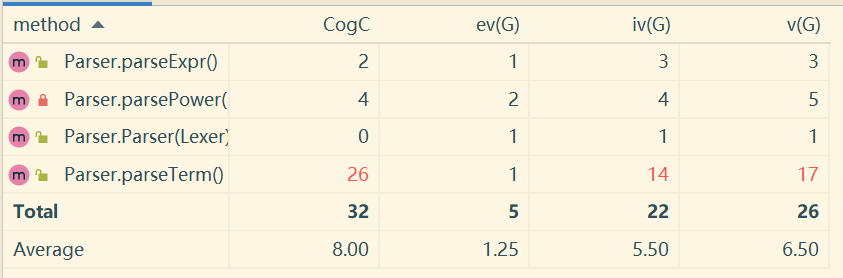
Parser类主要的圈复杂度问题在于parseTerm方法。与Func类中的replaceDeep方法类似,parseTerm也是直接处理字符串的方法,因此parseTerm中也存在大量的分支判断。事实上,我认为parseTerm方法是整个代码最混乱、最危险的部分,我一直想要用更加清晰的方式来替代Parser+Lexer的组合,但是很难做到。由于表达式的复杂性,我们没法单单用 +-* 来分割表达式并且递归处理,还是需要依靠一点点的顺序读入、解析。当然,即使没法做大的改变,一些小的圈复杂度的优化还是可以做的,比如把一个分支中的代码全部放在一个私有方法中调用。
bug分析
多亏了大家的帮助,在三次强测和互测中没有出现bug,那我就介绍一下课下出现的bug和互测的思路。
第一次作业
第一次作业有两个bug最难调,一个是Expr幂次时的克隆问题,另一个是Parser解析时的递归问题。
当我们想求出一个Expr类型的幂次的时候,往往出现这种情况:
Expr expr2 = expr;
for (int i = 1; i < index; i++) {
expr = expr * expr2;
}
然后就会发现 x**3 变成了 x**4,因为没有重写cloneable接口,只是浅克隆。当然,这一部分并不推荐写深克隆,而是直接声明一个值为1的Expr类型用来做乘法,既避免了上述问题,又能解决 index == 0 的情况。
另一个Parser解析时的递归问题,其实就是调用Lexer类的next方法的时机。如果next的时机不对,就可能出现这种情况:明明只是跳出了几层执行完的递归,curToken却往后跑了很远。这个时机很难把握,平心而论,如果让我再写一次作业,我相信还会在这上面栽跟头。
第二次作业
第二次作业主要说一下暴力replace会遇到的一些坑。
第一个是绝对不能用split偷懒。虽然split理论上能够完成第二次作业,但是面对函数嵌套就完全没用了,属于是零扩展性。对于自定义函数参数的获取,可以使用类似于栈的方式,在架构部分已经提到过了。
第二个是自变量和函数名存在冲突的问题,比如说 i 和sin。这个问题的解决就比较旁门左道了,直接把函数名替换成全大写字母,完成替换之后再换回来。
第三个是替换x的时候把其他自变量的替换结果也给替换了。比如说:
f(y,x) = x + y
f(x,2)
f(x,x) = x + x //代入y = x
f(x,2) = 4 //代入x = 2
这种情况也好办,可以强制先替换x,也可以把x换成大写保护起来,最后只替换大写的X。
第三次作业
第三次作业课下改动较少,bug也不是很有特点。但是再互测的时候找到一些bug。
第一个是众所周知的sum函数的 i 的取值可以是爆 int 的问题。
第二个是sin(0)直接不输出的问题。
关于Hack的策略,我个人是没有能力把房里的人代码都读一遍的,所以只能自己想一些极端情况和特殊情况,在Hack的时候,即使简单的例子也可能有奇效。
心得体会
第一单元的学习我收获了很多,学习了java很多的特性和数据结构,写过简洁漂亮的代码也写过臃肿复杂的玩意,有debug的痛苦,有过强测的欢乐,三人成行,见贤思齐。
而面向对象教给我最多的,还是思想,一种抽象与还原的思想。从现实的需求中抽象出来最根本的理念,即类。再从类出发还原出对象的关系和状态。我认为面向对象追求的是一种逻辑的自洽,如同小说家写作一般,要构建一个完美的画中世界。






 浙公网安备 33010602011771号
浙公网安备 33010602011771号