AGC052做题记录

A

其实是简单题，但我是唐诗。

\(2n\) 很简单，前 \(n\) 个和后 \(n\) 个全选 \(0/1\) 即可。可以感觉到正解只需要在这基础上改进，但是胡思乱想了很多没有任何进展。最后意识到最后凑个 \(0\) 即可。

B

做完 T1 ，就一直面对这道题罚坐，没有想到第一步。

边权化为点权， 每个点的点权是到根的路径上的边权异或和。（是否可以理解为树上的领域操作是区间操作，根链类似前缀和，所以变化的点只有 \(O(1)\)），那么操作等价于交换两个点权，所以合法的充要条件是 用\(w1,w2\) 算出的点权集合相等。

唯一的问题是和根交换，如果我们默认根点权是 \(0\) 的话不符合定义，但是我们只要求边两端的点权异或起来是边权即可，所以可以给根随便赋值。两棵树的根都可以随便赋，所以可以固定一个 \(w1\) 的根是 \(0\) ,判是否有合适的值，使第二个满足条件。点权集合相同的必要条件是点权和相同，有因为保证了 \(n\) 是奇数，所以可以直接算出来。因为不是充分的，所以再判一下是否合法即可。

C

困难题目。只会最暴力的 DP。

如果出现次数最多的数是 \(1\) 有 \(n-m\) 个，我们不（很）难发现答案的充要条件是 \(n-m\le \sum_{i=1}^m(p-b_i)+(p-1)\) 。必要性比较简单，因为总和大于 \((m+1)p\) ，跨过 \(p,2p,..,(m+1)p\) 时都需要一个不是 \(1\) 的数，不满足条件显然无解。

充分性有点困难，构造性证明。设当前的众数是 \(x\) ，和是 \(sum\) 。如果 \(sum+x\) 模 \(p\) 不等于 \(0\)，加入 \(x\)，否则加入 \(y\) 。然后最后不合法的答案一定形如：

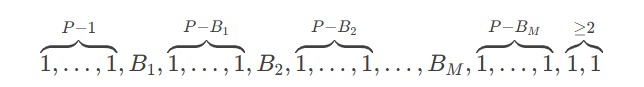
不难发现，这种情况不合法。

所以直接一个 dp 求出长度为 \(n\) 的和不为 \(0\) 的方案数，再用一个 dp \(f_{i,j}\) 表示 \(\sum_{k=1}^ip-b_k=j\) 的 \({B_1,...,B_i}\) 的数量，简单背包问题。答案是 \(\sum_{i=0}^N\sum_{j=0}f_{i,j}\binom{n}{i}(p-1)\)。（要满足和模 \(p\) 不等于 \(0\) ，且不满足上面的条件）。乘 \(\binom{n}{i}\) 表示选出不为 \(1\) 的位置，众数有 \(p-1\) 种取值所以还要乘 \(p-1\) （可以直接乘是因为将序列同时乘逆元一定一一对应）。不会算重是因为一定是绝对众数。

D

可以考虑原串的最长上升子序列。

不难发现，如果原串的 \(LIS=2k\) ，我们直接将 \(f_i\le k\) 分一组，剩下的分一组，那么两边的答案都是 \(k\) 。

否则 \(LIS=2k+1\) ，直接分不能直接相等，两部分的 \(LIS\) 至少是 \(k+1\) ，所以考虑凑限制最松的 \(k+1\) 。有结论是，只要能选出一个 \(x\) 不在这个上升子序列且满足存在一个长度为 \(k+1\) 的最长上升子序列包含 \(x\) ，就可构造出一组合法解。具体地，设这 \(k+1\) 个点下标是 \(i_1,i_2,...,i_{k+1}\) ，如果 \(\exists p,i_p\ne x,f_j=f_{i_p}\) 就放进第一组，否则就放进第二组，特殊地，将 \(x\) 放进第一组。这样分，第一组有 \(k+1\) 的上升子序列，且只有 \(k+1\) 中 \(f\) 值，所以不会有长为 \(k+2\) 的最长上升子序列，第二组有原串 LIS 的 \(k+1\) 点，同上可证答案为 \(k+1\) 。如果不存在，这样的节点，包含原串 LIS 少的一部分长度一定凑不出 \(k+1\) （可以简单反证）。

感觉思路是，\(f\) 值相同尽量放在一起，这样方便判断 \(LIS\) 。偶数直接做完了，奇数则需要将某个 \(f\) 中的一个值移动到另一个集合，使其长度加一，为了保证移动后这边还有 \(k+1\) 的，所以要找一个不在原 LIS 里的点。

E

有点类似的题目：AGC059E

我们可以将字母转化为数值，相邻字母不同，可以理解为数值模 \(3\) 之后的差一定是 \(1/-1\) 。

我们可以将一个合法字符串对应为一个数组，满足 \(|A_{i+1}-A_i|=1,A_i\equiv S_i\pmod 3\) 。固定 \(S\) 和 \(A_1\) 后，对应是唯一的。

现在思考一个操作，可以操作的位置，左右两边的值一定是相同的且变化的绝对值是 \(2\) 。如果我们已知 \(S,T\) 对应出的数组，如何算操作次数（因为都可以同时加 \(3\)，所以固定 \(A\) 的值，但 \(B\) 可以平移 ）。首先必要条件是和的奇偶相同，因为每次的变化值是 \(2/-2\) 不影响奇偶。（只用保证 \(A_1\equiv B_1 \pmod 2\) 即可）。答案的下界是 \({1\over 2}\sum_{i=1}^n|A_i-B_i|\) ，考虑证明答案一定可以取到下界，即每次一定可以有一个合法的操作位置。

如果存在 \(A_i>B_i\) 左右一定是 \(A_{i-1}\ge B_{i-1},A_{i+1}\ge B_{i+1}\) ，因为如果是 \(A_{i-1}<B_{i-1}\) 则 \(B\) 相邻的差大于 \(2\) 。所以有 \(A_{i-1}=A_{i+1}=A_i-1\) ,考虑反证如果 \(A_{i-1}=A_i+1\)，有 \(B_{i-1}\le B_{i}+1<A_i+1=A_{i-1}\) 所以 \(i-1\) 也符合条件且 \(A_{i-1}>A_i\) 与 \(A_i\) 的最大矛盾，所以不存在。（\(A_i<B_i\) 基本相同，找最小的即可）。

所以问题变为我们可以将 \(B\) 整体加 \(6\) 或减 \(6\) 使 \(\sum|A_i-B_i|\) 最小。设 \(C_i=A_i-B_i\) ,问题则是 \(\min_{y}\sum|C_i-6y|\) , 可以理解为 \(C\) 对应到坐标上与 \(6y\) 的距离之和最小，找中位数即可。