对偶图初探

平面图

定义

可以在平面内画出一个图而边没有任何交叉（公共端点相交不算），则是平面图。这种画法叫平面表示。

性质

1. 设 \(G\) 是带 \(e\) 条边和 \(v\) 个顶点的连通平面简单图。设 \(r\) 为平面图表示中的面数，则 \(r=e-v+2\) 。（具体证明见离散6.7.2）

2. 每个平面图 \(G\) 都有一个与其对偶的平面图 \(G^*\) 。

对偶图

\(G^*\)中的每个点对应 \(G\) 中的一个面包含一个无界的面。

对于 \(G\) 中每个边属于平面 \(f_1,f_2\)，则 \(G^*\) 中有边 \((f_1,f_2)\)。特殊地，如果一条边只在一个面中建自环。

举个例子（下面就是一个对偶图，白点实边是原平面图，黑点虚边是对偶图）

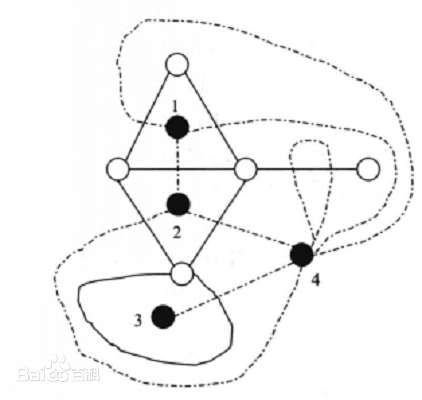
应用

对于题目特别强调是平面图或保证给出网格图(常见的平面图类型)之类的题目，可以思考转为对偶图来做。

网络流建模

P4001 [ICPC-Beijing 2006] 狼抓兔子 - 洛谷

上面的题，可以简单发现是最大流。但是直接做时间复杂度明面上是假的，这时我们发现题目有性质，是网格图 (平面图的一种) ，所以我们考虑建出原图对偶图 (要多连一个 \(s\) 到 \(t\) )。仔细观察后发现，去掉原图多连的边导致对偶图上多连的边但是不去掉点，在这个图上从起点（特殊建的点）到终点（无界的面对应得点）的一条路径对应原图的起点-终点的割。（其实是不去掉边的最小环)

要求最大流，就是求最小割，所以我们将每条边的长度赋为容量，则最小割的容量就是最短路的长度。求最短路就可以上堆优化 \(Dijkstra\) ，总时间复杂度 \(O(n\log^2n)\) 来求解特殊图的网络流。

总结一下，最大流等于最小割，最小割等于对偶图上的(去掉一条边之后的最短路/不去边的环）。

连通性相关

P10665 [AMPPZ2013] Bytehattan - 洛谷

对原图搞出对偶图的点，将删原图边变成加对偶图边。

一旦删去边后 \(u,v\) 不连通，就说明从 \(u,v\) 被割开了，就说明在有一个割的边都被选了。因为一个最小割就对应对偶图上的一个环，所以删完出现环就不连通，否则就连通。

资料

1. (浅析最大最小定理在信息学竞赛中的应用 - 百度文库)
2. 离散数学第八版