「IOI2021Day1T1」分糖果

直接用数据结构做，无论是势能线段树或是分块都难以维护。所以考虑数据结构维护对于固定糖果盒，每个时刻的修改情况。

传统的做法是每个时刻单独维护一个数据结构，数据结构存有每个糖果盒的信息。这里我们改成每个糖果盒单独维护一个数据结构，数据结构存有每个时刻的信息。

用线段树维护，假设当前只考虑盒子 \(i\) 有关的修改。以时间为下标，记下如果没有取 \(\max,\min\)，每个时刻 \(i\) 内有多少颗糖，也即修改量的前缀和。

我们把糖果盒满叫做碰上界，糖果盒空叫做碰下界。初始时，每个盒子都是空的，我们认为这算一次碰下界。如果碰上界后经过若干次修改，还没碰下界就又碰了上界，我们只把后面那次称作碰上界。下界同理。

那么我们用一个图像表示盒子内的糖数就是这样：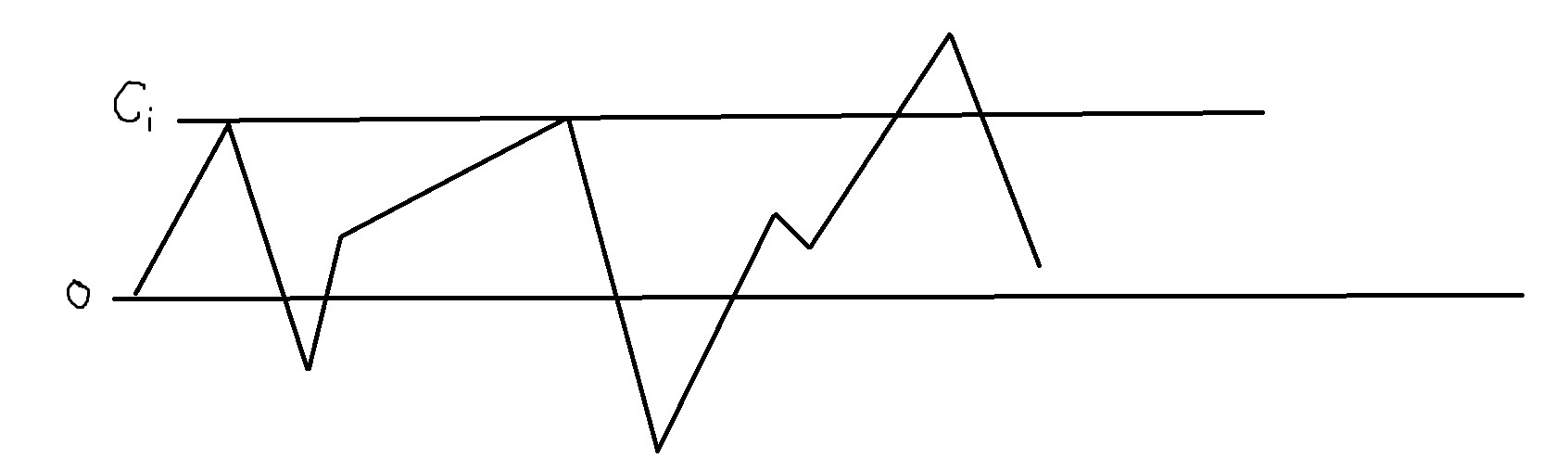

\(0\) 就是下界，\(c_i\) 就是上界。折线表示不考虑 \(\max,\min\) 的糖数（为了方便，称 \(i\) 时刻不考虑 \(\max,\min\) 的糖数为 \(s_i\)），横轴为时间轴，纵轴为数量。

如果我们想要知道最后的值，显然只需要知道最后一次碰上/下界的位置。

显然，如果区间内 \(s\) 极差 \(\ge c_i\)，则区间内必定包含最后两次碰上/下界。然后就可以找出最后一次，进而求出答案。所以线段树上二分就可以了。

由这题得出的一个经验是，当某些动态数据结构问题直接做难以维护时，可以考虑离线，对每个对象（如本题中的糖果盒）分开考虑，用一些数据结构维护时间轴上每一次修改。

#include "candies.h"
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cstdlib>
typedef int INT;
#define int long long

inline int min(const int x, const int y) {return x < y ? x : y;}
inline int max(const int x, const int y) {return x > y ? x : y;}
struct Line {
	int l, r, v, tim;
	inline bool operator < (const Line a) const {return l < a.l;}
} a[200005], b[200005];
inline bool cmp(Line a, Line b) {return a.r < b.r;}

std::vector<INT> ans;
int q;
struct Node {
	int l, r, mi, mx, tag;
} tree[800005];
void build(int O, int L, int R) {
	tree[O].l = L, tree[O].r = R;
	if (L != R) build(O << 1, L, L + R >> 1), build(O << 1 | 1, (L + R >> 1) + 1, R);
}
void pushdown(int O) {
	tree[O << 1].mi += tree[O].tag, tree[O << 1].mx += tree[O].tag;
	tree[O << 1].tag += tree[O].tag;
	tree[O << 1 | 1].mi += tree[O].tag, tree[O << 1 | 1].mx += tree[O].tag;
	tree[O << 1 | 1].tag += tree[O].tag;
	tree[O].tag = 0;
}
void update(int O, int p, int v) {
	if (p <= tree[O].l) {
		tree[O].mi += v, tree[O].mx += v, tree[O].tag += v;
		return;
	}
	pushdown(O);
	int mid = tree[O].l + tree[O].r >> 1;
	if (p <= mid) update(O << 1, p, v);
	update(O << 1 | 1, p, v);
	tree[O].mx = max(tree[O << 1].mx, tree[O << 1 | 1].mx);
	tree[O].mi = min(tree[O << 1].mi, tree[O << 1 | 1].mi);
}
int getsum() {
	int p = 1;
	while (tree[p].l != tree[p].r) pushdown(p), p = p << 1 | 1;
	return tree[p].tag;
}
int query(int O, int mi, int mx, int c) {
	if (tree[O].l == tree[O].r) {
		mi = min(mi, tree[O].tag), mx = max(mx, tree[O].tag);
		if (tree[O].tag == mi) return getsum() + c - mx;
		else return getsum() - mi;
	}
	pushdown(O);
	int mi2 = min(mi, tree[O << 1 | 1].mi), mx2 = max(mx, tree[O << 1 | 1].mx);
	if (mx2 - mi2 >= c) return query(O << 1 | 1, mi, mx, c);
	else return query(O << 1, mi2, mx2, c);
}

std::vector<INT> distribute_candies(std::vector<INT> c, std::vector<INT> l, std::vector<INT> r,
std::vector<INT> v) {
	int n = (int)c.size();
	q = (int)l.size();
	build(1, 0, q);
	for (int i = 1; i <= q; ++ i) a[i] = b[i] = Line{l[i - 1], r[i - 1], v[i - 1], i};
	std::sort(a + 1, a + q + 1);
	std::sort(b + 1, b + q + 1, cmp);
	for (int T = 0, i = 1, j = 1; T < n; ++ T) {
		while (i <= q && a[i].l <= T) update(1, a[i].tim, a[i].v), ++ i;
		while (j <= q && b[j].r < T) update(1, b[j].tim, -b[j].v), ++ j;
		if (tree[1].mx - tree[1].mi <= c[T]) ans.push_back(getsum() - tree[1].mi);
		else ans.push_back(query(1, 1e18, -1e18, c[T]));
	}
	return ans;
}