算法导论笔记（五）

第十二章：二叉查找树

摘要：

　　本章介绍了二叉查找树的概念及操作。主要内容包括二叉查找树的性质，如何在二叉查找树中查找最大值、最小值和给定的值，如何找出某一个元素的前驱和后继，如何在二叉查找树中进行插入和删除操作。在二叉查找树上执行这些基本操作的时间与树的高度成正比，一棵随机构造的二叉查找树的期望高度为O(lgn)，从而基本动态集合的操作平均时间为θ(lgn)。

1、二叉查找树

　　二叉查找树是按照二叉树结构来组织的，因此可以用二叉链表结构表示。二叉查找树中的关键字的存储方式满足的特征是：设x为二叉查找树中的一个结点。如果y是x的左子树中的一个结点，则key[y]≤key[x]。如果y是x的右子树中的一个结点，则key[x]≤key[y]。根据二叉查找树的特征可知，采用中根遍历一棵二叉查找树，可以得到树中关键字有小到大的序列。http://www.cnblogs.com/Anker/archive/2013/01/27/2878594.html介绍了二叉树概念及其遍历。一棵二叉树查找及其中根遍历结果如下图所示：

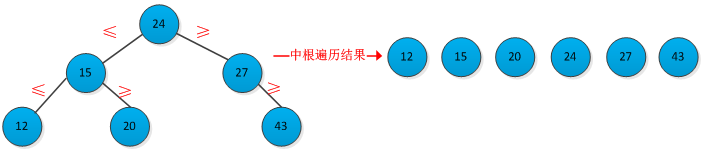
书中给出了一个定理：如果x是一棵包含n个结点的子树的根，则其中根遍历运行时间为θ(n)。

问题：二叉查找树性质与最小堆之间有什么区别？能否利用最小堆的性质在O(n)时间内，按序输出含有n个结点的树中的所有关键字？

2、查询二叉查找树

　　二叉查找树中最常见的操作是查找树中的某个关键字，除了基本的查询，还支持最大值、最小值、前驱和后继查询操作，书中就每种查询进行了详细的讲解。

（1）查找SEARCH

　　在二叉查找树中查找一个给定的关键字k的过程与二分查找很类似，根据二叉查找树在的关键字存放的特征，很容易得出查找过程：首先是关键字k与树根的关键字进行比较，如果k大比根的关键字大，则在根的右子树中查找，否则在根的左子树中查找，重复此过程，直到找到与遇到空结点为止。例如下图所示的查找关键字13的过程：（查找过程每次在左右子树中做出选择，减少一半的工作量）

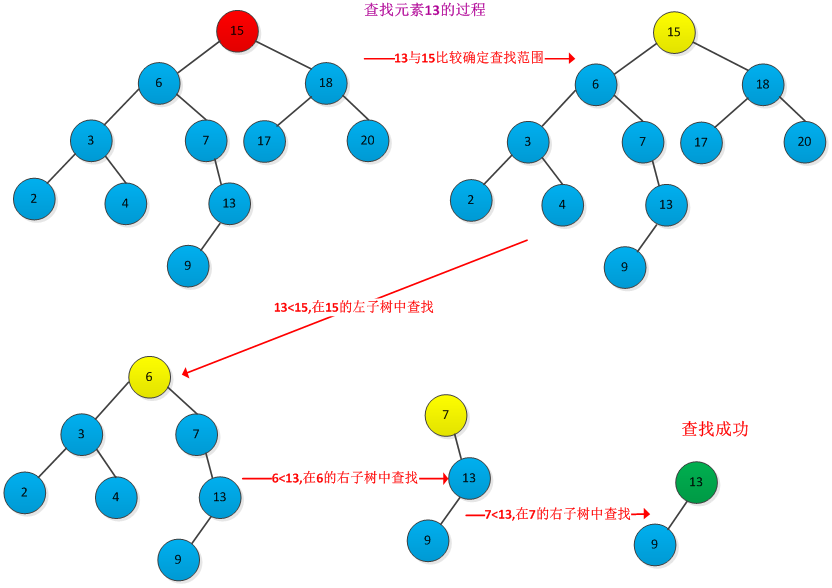
书中给出了查找过程的递归和非递归形式的伪代码：

TREE_SEARCH(x,k)
  if x=NULL or k=key[x]
      then return x
  if(k<key[x])
      then return TREE_SEARCH(left[x],k)
   else
      then return TREE_SEARCH(right[x],k)

　　

ITERATIVE_TREE_SEARCH(x,k)
  while x!=NULL and k!=key[x]
      do if k<key[x]
              then x=left[x]
           else
              then x=right[x]
   return x

（2）查找最大关键字和最小关键字

　　根据二叉查找树的特征，很容易查找出最大和最小关键字。查找二叉树中的最小关键字：从根结点开始，沿着各个节点的left指针查找下去，直到遇到NULL时结束。如果一个结点x无左子树，则以x为根的子树中，最小关键字就是key[x]。查找二叉树中的最大关键字：从根结点开始，沿着各个结点的right指针查找下去，直到遇到NULL时结束。书中给出了查找最大最小关键字的伪代码：

TREE_MINMUM(x)
   while left[x] != NULL
      do x=left[x]
   return x

　　

TREE_MAXMUM(x)
   while right[x] != NULL
        do x= right[x]
    return x

（3）前驱和后继

　　给定一个二叉查找树中的结点，找出在中序遍历顺序下某个节点的前驱和后继。如果树中所有关键字都不相同，则某一结点x的前驱就是小于key[x]的所有关键字中最大的那个结点，后继即是大于key[x]中的所有关键字中最小的那个结点。根据二叉查找树的结构和性质，不用对关键字做任何比较，就可以找到某个结点的前驱和后继。

　　查找前驱步骤：先判断x是否有左子树，如果有则在left[x]中查找关键字最大的结点，即是x的前驱。如果没有左子树，则从x继续向上执行此操作，直到遇到某个结点是其父节点的右孩子结点。例如下图查找结点7的前驱结点6过程：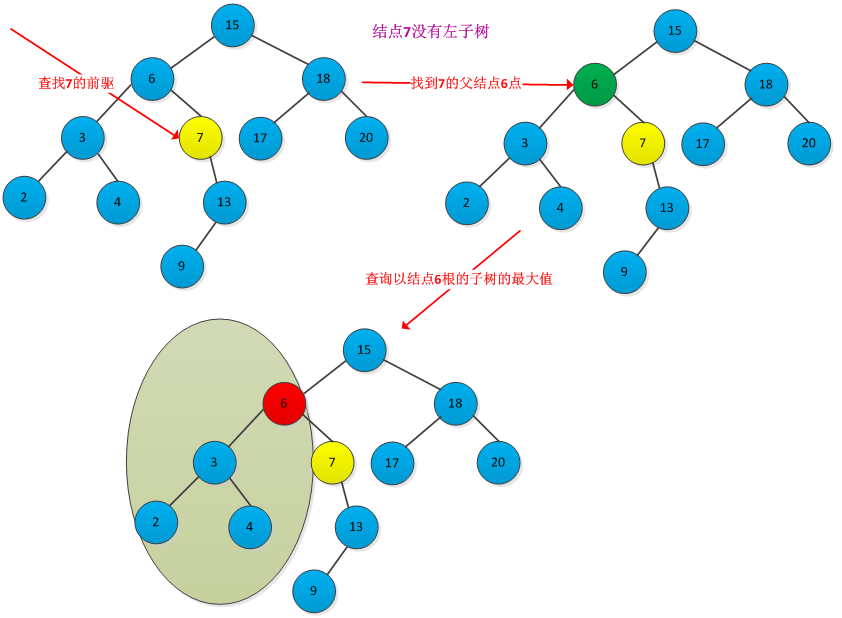

　　查找后继步骤：先判断x是否有右子树，如果有则在right[x]中查找关键字最小的结点，即使x的后继。如果没有右子树，则从x的父节点开始向上查找，直到遇到某个结点是其父结点的左儿子的结点时为止。例如下图查找结点13的后继结点15的过程：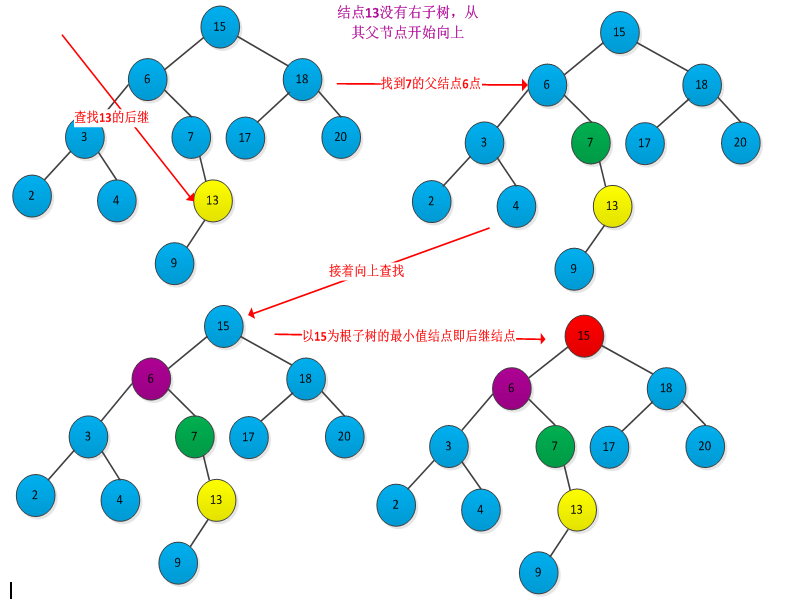

书中给出了求x结点后继结点的伪代码:

TREE_PROCESSOR(x)
   if right[x] != NULL
       then return TREE_MINMUM(right(x))
   y=parent[x]
   while y!= NULL and x ==right[y]
          do x = y
              y=parent[y]
   return y

定理：对一棵高度为h的二叉查找，动态集合操作SEARCH、MINMUM、MAXMUM、SUCCESSOR、PROCESSOR等的运行时间均为O(h)。

3、插入和删除

　　插入和删除会引起二叉查找表示的动态集合的变化，难点在在插入和删除的过程中要保持二叉查找树的性质。插入过程相当来说要简单一些，删除结点比较复杂。

（1）插入

　　插入结点的位置对应着查找过程中查找不成功时候的结点位置，因此需要从根结点开始查找带插入结点位置，找到位置后插入即可。下图所示插入结点过程：

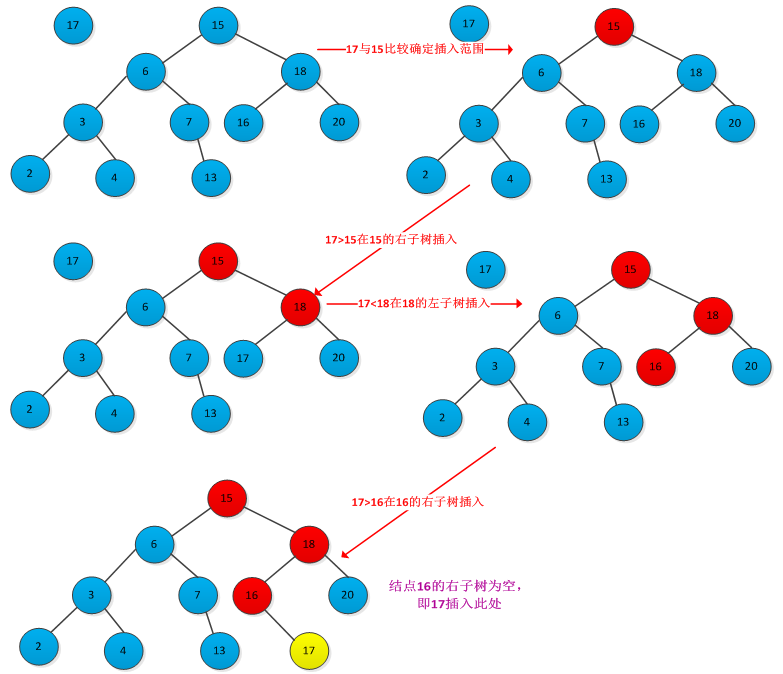
书中给出了插入过程的伪代码：

TREE_INSERT(T,z)
    y = NULL;
    x =root[T]
    while x != NULL
        do y =x
            if key[z] < key[x]
                 then x=left[x]
                 else  x=right[x]
     parent[z] =y
     if y=NULL
        then root[T] =z
        else if key[z]>key[y]
                   then  keft[y]  = z
                   else   right[y] =z

插入过程运行时间为O(h)，h为树的高度。

（2）删除

　　从二叉查找树中删除给定的结点z，分三种情况讨论：

<1>结点z没有左右子树，则修改其父节点p[z]，使其为NULL。删除过程如下图所示：

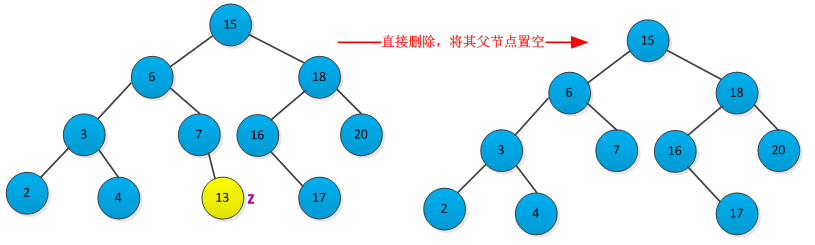
<2>如果结点z只有一个子树（左子树或者右子树），通过在其子结点与父节点建立一条链来删除z。删除过程如下图所示：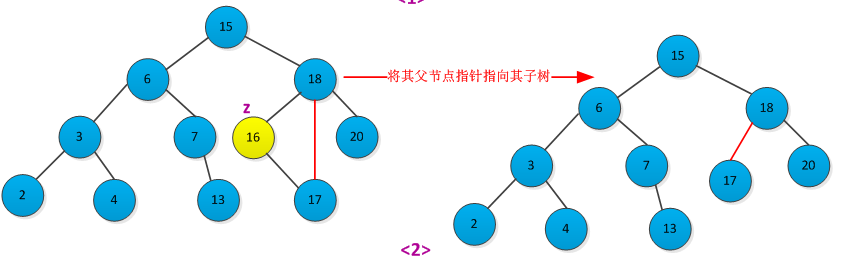

<3>如果z有两个子女，则先删除z的后继y（y没有左孩子），在用y的内容来替代z的内容。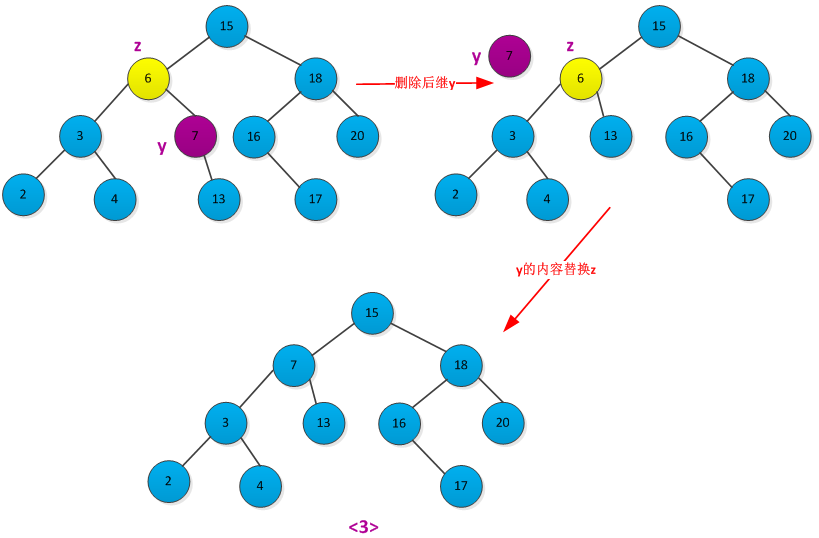

书中给出了删除过程的伪代码：

TREE_DELETE(T,z)
    if left[z] ==NULL or right[z] == NULL
       then y=z
       else  y=TREE_SUCCESSOR(z)
   if left[y] != NULL
       then x=left[y]
       else  x=right[y]
   if x!= NULL
       then parent[x] = parent[y]
   if p[y] ==NULL
      then root[T] =x
      else if y = left[[prarnt[y]]
                  then left[parent[y]] = x
                  else  right[parent[y]] =x
    if y!=z
        then key[z] = key[y]
              copy y's data into z
     return y        

定理：对高度为h的二叉查找树，动态集合操作INSERT和DELETE的运行时间为O(h)。

4、实现测试

　　采用C++语言实现一个简单的二叉查找树，支持动态集合的基本操作：search、minmum、maxmum、predecessor、successor、insert和delete。设计的二叉查找树结构如下所示：

template <class T>
class  BinarySearchTreeNode
{
public:
    T elem;
    struct BinarySearchTreeNode<T> *parent;
    struct BinarySearchTreeNode<T>* left;
    struct BinarySearchTreeNode<T>* right;
};

template <class T>
class BinarySearchTree
{
public:
    BinarySearchTree();
    void tree_insert(const T& elem);
    int  tree_remove(const T& elem );
    BinarySearchTreeNode<T>* tree_search(const T& elem)const;
    T tree_minmum(BinarySearchTreeNode<T>* root)const;
    T tree_maxmum(BinarySearchTreeNode<T>* root)const;
    T tree_successor(const T& elem) const;
    T tree_predecessor(const T& elem)const;
    int empty() const;
    void inorder_tree_walk()const;
    BinarySearchTreeNode<T>* get_root()const {return root;}
private:
    BinarySearchTreeNode<T>* root;
};

　　

 完整程序如下所示：

#include <iostream>
#include <stack>
#include <cstdlib>
using namespace std;

template <class T>
class  BinarySearchTreeNode
{
public:
    T elem;
    struct BinarySearchTreeNode<T> *parent;
    struct BinarySearchTreeNode<T>* left;
    struct BinarySearchTreeNode<T>* right;
};

template <class T>
class BinarySearchTree
{
public:
    BinarySearchTree();
    void tree_insert(const T& elem);
    int  tree_remove(const T& elem );
    BinarySearchTreeNode<T>* tree_search(const T& elem)const;
    T tree_minmum(BinarySearchTreeNode<T>* root)const;
    T tree_maxmum(BinarySearchTreeNode<T>* root)const;
    T tree_successor(const T& elem) const;
    T tree_predecessor(const T& elem)const;
    int empty() const;
    void inorder_tree_walk()const;
    BinarySearchTreeNode<T>* get_root()const {return root;}
private:
    BinarySearchTreeNode<T>* root;
};

template <class T>
BinarySearchTree<T>::BinarySearchTree()
{
    root = NULL;
}

template <class T>
void BinarySearchTree<T>::tree_insert(const T& elem)
{
    if(!empty())
    {
        BinarySearchTreeNode<T> *pnode = root;
        BinarySearchTreeNode<T> *qnode = NULL;
        BinarySearchTreeNode<T> *newnode = new BinarySearchTreeNode<T>;
        newnode->elem = elem;
        newnode->parent = NULL;
        newnode->left = NULL;
        newnode->right = NULL;
        while(pnode)
        {
            qnode = pnode;
            if(pnode->elem > elem)
                pnode = pnode->left;
            else
                pnode = pnode->right;
        }
        if(qnode->elem > elem)
            qnode->left = newnode;
        else
            qnode->right = newnode;
        newnode->parent = qnode;
    }
    else
    {
        root = new BinarySearchTreeNode<T>;
        root->elem = elem;
        root->parent =NULL;
        root->left = NULL;
        root->right = NULL;
    }
}

template <class T>
int BinarySearchTree<T>::tree_remove(const T&elem)
{
    BinarySearchTreeNode<T> *pnode;
    BinarySearchTreeNode<T> *parentnode,*snode;
    pnode = tree_search(elem);
    if(pnode != NULL)
    {
       parentnode = pnode->parent;
       if(pnode->right == NULL || pnode->left == NULL)
       {
            if(pnode->right != NULL)
            {
                if(parentnode->left == pnode)
                    parentnode->left = pnode->right;
                if(parentnode->right == pnode)
                    parentnode->right = pnode->right;
                pnode->right->parent = parentnode;
            }
            else if(pnode->left != NULL)
            {
                if(parentnode->left == pnode)
                    parentnode->left = pnode->left;
                if(parentnode->right == pnode)
                    parentnode->right = pnode->left;
                pnode->left->parent = parentnode;
            }
            else
            {
                if(parentnode->left == pnode)
                    parentnode->left = NULL;
                if(parentnode->right == pnode)
                    parentnode->right = NULL;
            }
            delete pnode;
       }
       else
       {
           snode = tree_search(tree_successor(pnode->elem));
           pnode->elem = snode->elem;
           if(snode->parent->left == snode)
           {
               snode->parent->left = snode->right;
               snode->right->parent = snode->parent->left;
           }
           if(snode->parent->right == snode)
           {
               snode->parent->right = snode->right;
               snode->right->parent = snode->parent->right;
           }
           delete snode;
       }
       return 0;
    }
    return -1;
}
template <class T>
BinarySearchTreeNode<T>* BinarySearchTree<T>::tree_search(const T& elem)const
{
    BinarySearchTreeNode<T> *pnode = root;
    while(pnode)
    {
        if(pnode->elem == elem)
            break;
        else if(pnode->elem > elem)
            pnode = pnode->left;
        else
            pnode = pnode->right;
    }
    return pnode;
}

template <class T>
T BinarySearchTree<T>::tree_minmum(BinarySearchTreeNode<T>* root)const
{
    BinarySearchTreeNode<T> *pnode = root;
    if(pnode->left)
    {
        while(pnode->left)
            pnode = pnode->left;
    }
    return pnode->elem;
}

template <class T>
T BinarySearchTree<T>::tree_maxmum(BinarySearchTreeNode<T>* root)const
{
    BinarySearchTreeNode<T> *pnode = root;
    if(pnode->right)
    {
        while(pnode->right)
           pnode = pnode->right;
    }
    return pnode->elem;
}

template <class T>
T BinarySearchTree<T>::tree_successor(const T& elem) const
{
    BinarySearchTreeNode<T>* pnode = tree_search(elem);
    BinarySearchTreeNode<T>* parentnode;
    if(pnode != NULL)
    {
        if(pnode->right)
            return tree_minmum(pnode->right);
        parentnode = pnode->parent;
        while(parentnode && pnode == parentnode->right)
        {
            pnode = parentnode;
            parentnode = parentnode->parent;
        }
        if(parentnode)
            return parentnode->elem;
        else
            return T();
    }
    return T();
}
template <class T>
T BinarySearchTree<T>::tree_predecessor(const T& elem)const
{
    BinarySearchTreeNode<T>* pnode = tree_search(elem);
    BinarySearchTreeNode<T>* parentnode;
    if(pnode != NULL)
    {
        if(pnode->right)
            return tree_maxmum(pnode->right);
        parentnode = pnode->parent;
        while(parentnode && pnode == parentnode->left)
        {
            pnode = parentnode;
            parentnode = pnode->parent;
        }
        if(parentnode)
            return parentnode->elem;
        else
            return T();
    }
    return T();
}

template <class T>
int BinarySearchTree<T>::empty() const
{
    return (NULL == root);
}

template <class T>
void BinarySearchTree<T>::inorder_tree_walk()const
{
    if(NULL != root)
     {
         stack<BinarySearchTreeNode<T>*> s;
         BinarySearchTreeNode<T> *ptmpnode;
         ptmpnode = root;
        while(NULL != ptmpnode || !s.empty())
        {
             if(NULL != ptmpnode)
             {
                 s.push(ptmpnode);
                 ptmpnode = ptmpnode->left;
             }
            else
            {
                ptmpnode = s.top();
                s.pop();
                cout<<ptmpnode->elem<<" ";
                ptmpnode = ptmpnode->right;
            }
         }
      }
}
int main()
{
    BinarySearchTree<int> bstree;
    BinarySearchTreeNode<int>* ptnode,*proot;
    bstree.tree_insert(32);
    bstree.tree_insert(21);
    bstree.tree_insert(46);
    bstree.tree_insert(54);
    bstree.tree_insert(16);
    bstree.tree_insert(38);
    bstree.tree_insert(70);
    cout<<"inorder tree walk is: ";
    bstree.inorder_tree_walk();
    proot = bstree.get_root();
    cout<<"\nmax value is: "<<bstree.tree_maxmum(proot)<<endl;
    cout<<"min value is: "<<bstree.tree_minmum(proot)<<endl;
    ptnode = bstree.tree_search(38);
    if(ptnode)
        cout<<"the element 38 is exist in the binary tree.\n";
    else
        cout<<"the element 38 is not exist in the binary tree.\n";
    cout<<"the successor of 38 is: "<<bstree.tree_successor(38)<<endl;
    cout<<"the predecessor of 38 is:"<<bstree.tree_predecessor(38)<<endl;
    if(bstree.tree_remove(46) == 0)
        cout<<"delete 46 successfully"<<endl;
    else
        cout<<"delete 46 failed"<<endl;
    cout<<"inorder tree walk is: ";
    bstree.inorder_tree_walk();
    exit(0);
}

　　

程序测试结果如下所示：

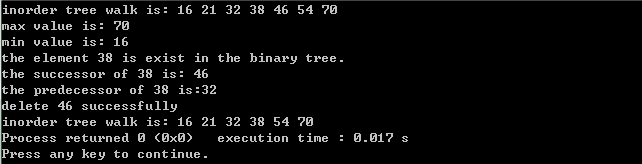
　　二叉树实现时候添加了一个父结点指针，方便寻找给定结点的前驱和后继。二叉树中删除操作实现比较复杂，需要分类讨论，我分三种情况进行讨论，程序写的有些繁琐，可以进行优化。优化后的代码如下：

template <class T>
int BinarySearchTree<T>::tree_delete(const T& elem)
{
    //找到该元素对应的结点
    BinarySearchTreeNode<T>* pnode = tree_search(elem);
    if(NULL != pnode)
    {
        BinarySearchTreeNode<T> *qnode,*tnode;
        //判断结点是否有左右孩子
        if(pnode->left == NULL || pnode->right == NULL)
            qnode = pnode;   //有一个左孩子或者一个右孩子和没有左右孩子
        else
            qnode = tree_search(tree_successor(elem)); //有左右孩子
        if(NULL != qnode->left)
            tnode = qnode->left;
        else
            tnode = qnode->right;
        if(NULL != tnode)
            tnode->parent = qnode->parent;
        if(qnode->parent == NULL)
            root = tnode;
        else
            if(qnode == qnode->parent->left)
                qnode->parent->left = tnode;
            else
                qnode->parent->right = tnode;
        if(qnode != pnode)
            pnode->elem = qnode->elem;  //将后继结点的值复制到要删除的结点的值
        delete qnode;
        return 0;
    }
    return -1;
}

　　

5、随机构造二叉查找树

　　二叉查找上各种基本操作的运行时间都是O(h)，h为树的高度。但是在元素插入和删除过程中，树的高度会发生改变。如果n个元素按照严格增长的顺序插入，那个构造出的二叉查找树的高度为n-1。例如按照先后顺序插入7、15、18、20、34、46、59元素构造二叉查找树，二叉查找树结构如下所示：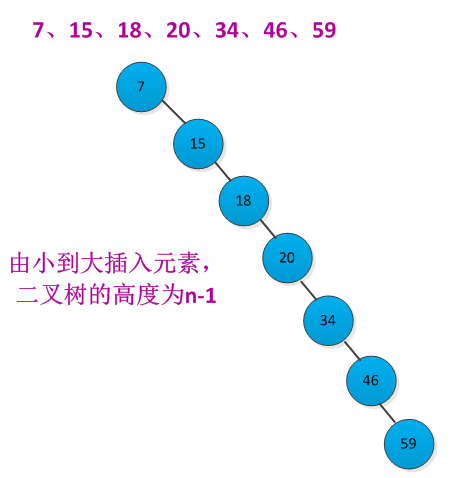

 第十三章：红黑树

摘要：

　　红黑树是一种二叉查找树，但在每个结点上增加了一个存储位表示结点的颜色，可以是RED或者BLACK。通过对任何一条从根到叶子的路径上各个着色方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，因而是接近平衡的。本章主要介绍了红黑树的性质、左右旋转、插入和删除。重点分析了在红黑树中插入和删除元素的过程，分情况进行详细讨论。一棵高度为h的二叉查找树可以实现任何一种基本的动态集合操作，如SEARCH、PREDECESSOR、SUCCESSOR、MIMMUM、MAXMUM、INSERT、DELETE等。当二叉查找树的高度较低时，这些操作执行的比较快，但是当树的高度较高时，这些操作的性能可能不比用链表好。红黑树（red-black tree）是一种平衡的二叉查找树，它能保证在最坏情况下，基本的动态操作集合运行时间为O(lgn)。本章内容有些复杂，看了两天，才大概清楚其插入和删除过程，日后需要经常回顾，争取完全消化掉。红黑树的用途非常广泛，例如STL中的map就是采用红黑树实现的，效率非常之高，有机会可以研究一下STL的源代码。

1、红黑树的性质

　　红黑树中的每个结点包含五个域：color、key、left、right和parent。如果某结点没有一个子结点或父结点，则该结点相应的指针parent域包含值为NIL（NIL并是是空指针，此处有些迷惑，一会解释）。把NIL视为指向红黑树的外结点（叶子）的指针，而把带关键字的结点视为红黑树的内结点。红黑树结点结构如下所示：

#define RED  0
#define BLACK 1
struct RedBlackTreeNode
{ 
    T key;
    struct RedBlackTreeNode * parent;
    struct RedBlackTreeNode * left;
    struct RedBlackTreeNode * right;
    int color;
};

　　

红黑树的性质如下：

（1）每个结点或是红色，或是黑色。

（2）根结点是黑色。

（3）每个叶子结点（NIL）是黑色。

（4）如果有一个结点是红色，则它的两个儿子都是黑色。

（5）对每个结点，从该结点到其孙子结点的所有路径上包含相同数目的黑色结点。

如下图是一棵红黑树：

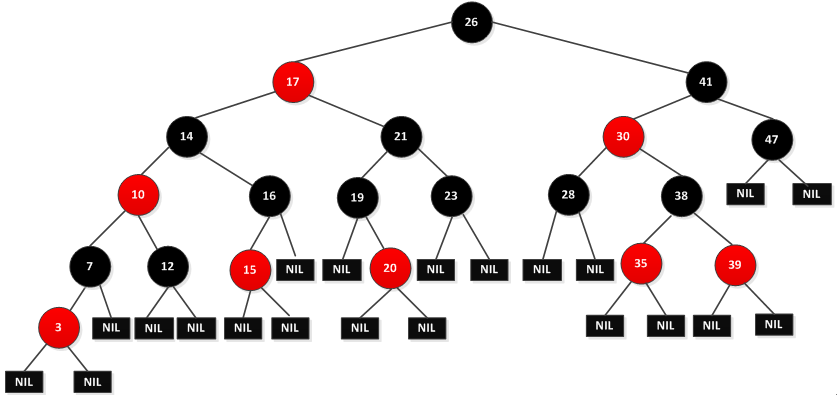
从图可以看出NIL不是空指针，而是一个叶子结点。实际操作的时候可以将NIL视为哨兵，这样便于对黑红色进行操作。红黑树的操作主要是对内部结点操作，因为内部结点存储了关键字的值。书中为了便于讨论，忽略了叶子结点的，如是上图红黑树变成如下图所示：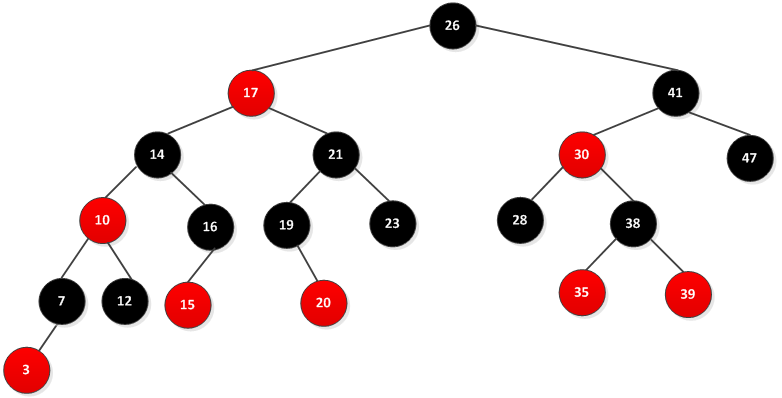

　　书中给出了黑高度的概念：从某个结点x出发（不包含该结点）到达一个叶子结点的任意一条路径上，黑色结点的个数称为该结点的黑高度。由红黑树的性质（5）可知，从该结点出发的所有下降路径都有相同的黑色结点个数。红黑树的黑高度定义为其根结点的黑高度。

　　书中给出了一个引理来说明为什么红黑树是一种好的查找树，并对引理进行了证明（采用归纳法进行证明的，需要很强的归纳推理知识，正是我的不足之处，看书的痛苦在于此）。

引理：一棵有n个内结点的红黑树的高度之多为2lg(n+1)。

2、旋转

　　在红黑树上进行结点插入和删除操作时，会改变树的结构形状，导致结果可能不满足了红黑树的某些性质，为了保证每次插入和删除操作后，仍然能报维持红黑树的性质，需要改变树中某些结点的颜色和指针结构。其中的指针结构的改变通过旋转完成的。书中给出了两种旋转：左旋转和右旋转。如下图是旋转过程：

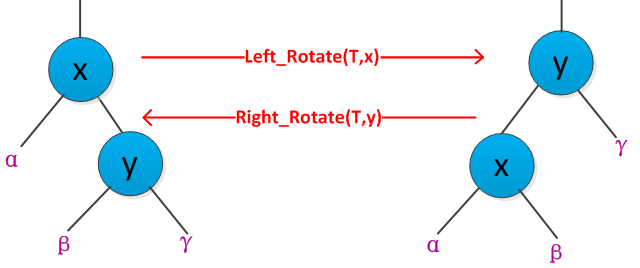
　　从图可以得出左右旋转的过程，假设对某个结点x进行左旋转，y是x的右孩子，则左旋转过程为：以x和y之间的链为“支轴”进行的，使得x的右孩子为y的左孩子，y的父节点为x的父节点，y的左孩子为x。书中给出了左旋转的伪代码如下：

LEFT_ROTATE(T,x)
   y = right[x]   //获取右孩子
   rihgt[x] = left[y]  //设置x的右孩子为y的左孩子
   if left[y] != NIL
       then parent[left[x]] = x
    parent[y] = parent[x]  //设置y的父节点为x的父节点
    if parent[x] == NIL
       then root[T] = y
       else if x==left[parent[x]
              then left[parent[x]] = y
              else  right[[parent[x]] = y
    left[y] = x  //设置y的左孩子为x
    parent[x] =y

  

假设对某个结点y进行右旋转，x是y的左孩子，则左旋转过程为：y的左孩子设置为x的右孩子，将x的父节点设置为y的父节点，x的右孩子设置为y。书中并没有给出右旋转的伪代码，参照左旋转的伪代码很容易实现：

RIGHT_ROTATE(T,y)
     x = left[y]    //获取左孩子
     left[y] = right[x] //设置y的左孩子为x的右孩子
     if right[x] != NIL
        then parent[right[x]] = y
     parent[x] = parent[y]  //设为x的父节点为y的父结点
     if parent[y] == NIL
         then root = x
         else if y== left[parent[y]]
               then left[parent[y]] = x
               else  right[parent[y]] = x
     right[x] = y //设置x的右孩子为y
     parent[y] = x

 为了更好的理解旋转操作，书中给出了一个左旋转的例如，如下图所示：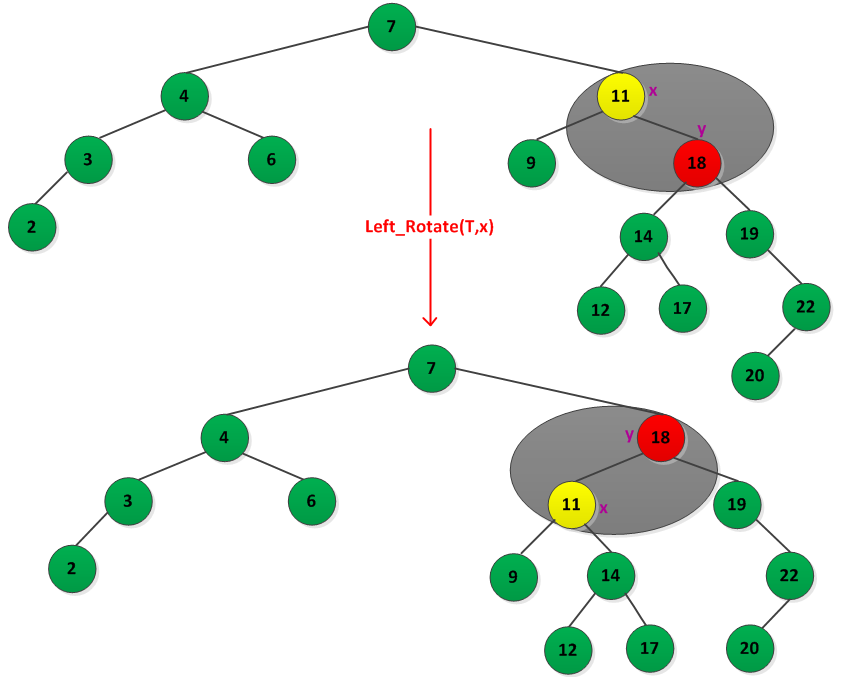

3、插入

　　红黑树插入一个新结点的过程RB_INSERT是在二叉查找树插入过程的基础上改进的，先按照二叉排序的插入过程插入到红黑树中，然后将新插入的结点标记为红色（疑问：为什么是红色，而不是黑色呢？），然后调用一个辅助的过程RB_INSERT_FIXUP来调整结点并重新着色，使得满足红黑树的性质。关于二叉查找树的插入过程可以参考上一篇日志：http://www.cnblogs.com/Anker/archive/2013/01/28/2880581.html。书中给出了RB_INSERT的伪代码：

RB_INSERT(T,z)
  y = NIL
  x =root(T)
  while x != NIL
       do y=x
           if key[z]<key[x]
             then x=left[x]
             else  x=right[x]
  parent[z] = y
  if y =NIL
     then root =z
     else if key[z] < key[y]
            then left[y] =z
            else  right[y] =z
   left[z] = NIL
   right[z] =NIL
   color[z] = RED  //新插入结点标记为红色
   RB_INSERT_FIXUP(T,z)  //进行调整，使得满足红黑树性质

　　红黑树的插入过程最主要的是RB_INSERT_FIXUP过程，书中发了很大的篇幅进行介绍。首先分析了当插入一个新的结点后，会破坏红黑树的哪些性质，然后针对可能的破坏性质进行分类讨论并给出了给出了解决办法。因为每次插入的新元素标记为RED，这样可能性质2（根节点为黑色）和性质4（一个红结点的左右孩子都是黑色的）被破坏。例如下图插入一个新结点，破坏了性质4。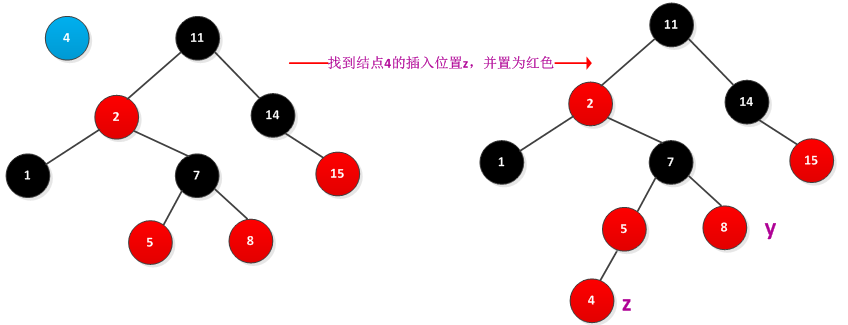

      如果每次插入新的结点z导致红黑树性质被破坏，则之多只有一个性质被破坏，并且不是性质2就是性质4。违反性质2是因为z是根且为红色，违反性质4是因为z和其父节点parent[z]都是红色的。

　　如果性质2被违反了，则红色的根必定是新增的结点z，它是树中唯一的内结点，由于z的父接点和两个子女都是NIL（黑色），不违反性质4。违反性质2在整个插入过程中只有这一次。所以对于违反性质2的结点，直接将其结点变成黑色即可。

　　剩下的问题是对于违反性质4的处理，在插入新结点z之前，红黑树的性质没有被破坏。插入结点z后违反性质4，必定是因为z和其父亲结点parent[z]都是红色的，此时只违反性质4，而没有违反其他性质。假设新插入结点z，导致红黑树性质4被破坏，此时z和其父节点parent[z]都是红色，由于在插入结点z之前红黑树的性质没有被破坏，parent[z]是红色，很容易推出z的祖父结点parent[parent[z]]必定是黑色。此时根据parent[z]是parent[parent[z]]的左孩子还是右孩子进行讨论。因为左右之间是对称的，书中只给出了parent[z]作为parent[parent[z]]的左孩子进行讨论的，然后给出了三种可能的情况。

情况1）：z的叔叔结点y是红色的

　　此时parent[z]和y都是红色的，解决办法是将z的父节点parent[z]和叔叔结点y都着为黑色，而将z的祖父结点parent[parent[z]]着为红色，然后从祖父结点parent[parent[z]]继续向上判断是否破坏红黑树的性质。处理过程如下图所示：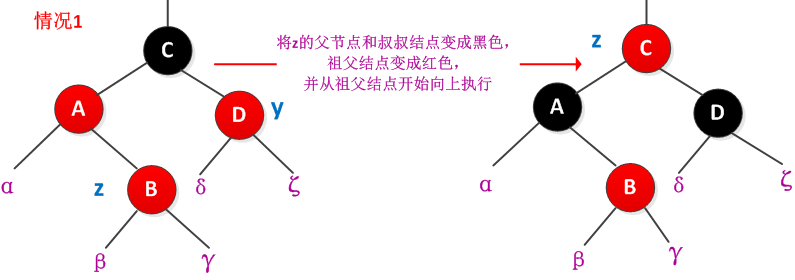

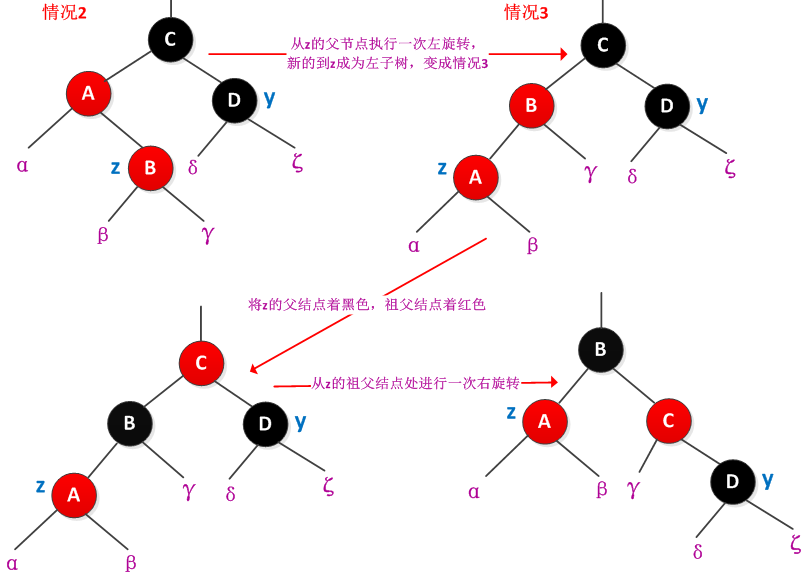
情况2）：z的叔叔y是黑色的，而且z是右孩子

情况3）：z的叔叔y是黑色的，而且z是左孩子

　　情况2和情况3中y都是黑色的，通过z是左孩子还是右孩子进行区分的。可以将情况2通过旋转为情况3。情况2中z是右孩子，旋转后成为情况3，使得z变为左孩子，可以在parent[z]结点出使用一次左旋转来完成。无论是间接还是直接的通过情况2进入到情况3，z的叔叔y总是黑色的。在情况3中，将parent[z]着为黑色，parent[parent[z]]着为红色，然后从parent[parent[z]]处进行一次右旋转。情况2、3修正了对性质4的违反，修正过程不会导致其他的红黑性质被破坏。修正过程如下图所示：

　　给一个完整的例子来说明插入过程，如下图所示：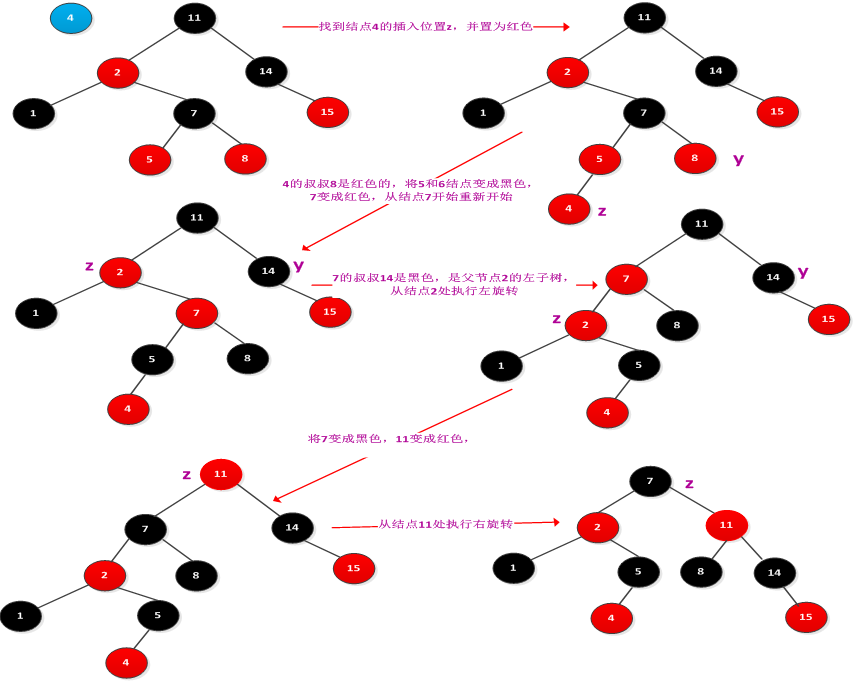

　　书中给出了RB_INSERT_FIXUP的伪代码，伪代码中只给出了z的父节点为左孩子的情况，为右孩子的情况与左孩子的情况是对称的，只需将左孩子中的right换成left即可。

RB_INSERT_FIXUP(T,z)
         while color[parent[z]] = RED
           do if parent[z] == left[parent[parent[z]]]
                  then y = right[parent[parent[z]]]
                       if color[y] == RED    //情况1，z的叔叔为红色
                            then color[parent[z]] = BLACK
                                 color[y] = BLACK
                                 color[parent[parent[z]]=RED 
                                 z= parent[parent[z]]
                                 else if z == right[parent[z]]    //情况2，z的叔叔为黑色，z为右孩子
                                       then z = parent[z]
                                            LEFT_ROTATE(T,z)
                                        color[parent[z]]=BLACK    //情况3，z的叔叔为黑色，z为左孩子
                                        color[parent[parent[z]] = RED
                                        RIGHT_ROTATE(T, parent[parent[z]])
                else (same as then clause with “right” and “left” exchanged)
  color(root(T)) = BLACK; //将根结点设置为黑色

4、删除

　　 删除过程最复杂，看了好多遍才明白个大概，需要反复看，多想删除过程中会破坏哪些性质，然后又针对性的去调整。

　　红黑树删除结点过程是在二叉查找树删除结点过程的基础改进的。与二叉查找树类似，删除的结点分为三种情况：<1>无左右孩子、<2>有左孩子或者右孩子、<3>既有树=左孩子又有右孩子。删除过程可以参考前一篇日志：http://www.cnblogs.com/Anker/archive/2013/01/28/2880581.html。红黑树在删除结点后需要检查是否破坏了红黑树的性质。如果删除的结点y是红色的，则删除后的树仍然是保持红黑树的性质，因为树中各个结点的黑高度没有改变，不存在两个相邻（父结点和子结点）的红色结点，y是红色不可能是根，所有根仍然是黑色。如果删除的结点z是黑色的，则这个是破坏了红黑树的性质，需要调用RB_DELETE_FIXUP进行调整。从删除结点y的唯一孩子结点x或者是NIL处开始调整。书中给出了RB_DELETE的伪代码：

RB_DELETE(T,z)
     if left[z] ==NIL or right[z] == NIL
        then y=z
        else  y=TREE_SUCCESSOR(z)
    if left[y] != NIL
        then x=left[y]
        else  x=right[y]
    parent[x] = parent[y]
    if p[y] ==NIL
       then root[T] =x
       else if y = left[[prarnt[y]]
                   then left[parent[y]] = x
                   else  right[parent[y]] =x
     if y!=z
         then key[z] = key[y]
               copy y's data into z
     if color[y] == BLACK    //当被删除结点为黑色时候进行调整
         then RB_DELETE_FIXUP(T,x)
      return y

　　书中分析了被删除结点y是黑色会产生的问题：首先，如果y是根，而y的一个红色孩子变成了新根，则违反了性质2。其次，如果x和parent[y]（此时parent[x] = parent[y]）都是红色，就违反了性质4。第三，删除y将会导致先前包含y的任何路径上黑结点个数减少1，违反了性质5。书中给出了解决第三个问题的办法：将结点x设为还有额外的一重黑色（此处看的不是很明白，我的理解是是不管是x是什么颜色，将x增加了额外一重黑色，这样可以保证黑结点数目增加1个），即将任意包含结点x的路径上黑结点个数加1，这样可以保证性质5成立。当将黑色结点y被删除时，将其黑色“下推”至其子结点，导致问题变成为结点x可能即不是红，又不是黑，从而违反性质1。因为给x增加了一种颜色，即结点x是双重黑色或者是红黑色。这样就分别给包含x的路径上黑结点个数贡献2个或1个。但是x的color属性仍然是RED（如果x是红黑的）或BLACK（如果x是双重黑色）。换而言之，一个结点额外的黑色反映在x指向它，而不是它的color属性。

　　过程RB_DELETE_FIXUP恢复性质1，2，4。对于恢复性质2、4很简单，因为x是红色，所有直接将x结点着为黑色即可。书中着重介绍了如何恢复性质1。此时x是黑色，需要根据x是左孩子还是右孩子两种情况进行恢复，因为左右是对称的，书中只给出了x是左孩子的恢复过程。将x作为第一个额外的黑色结点，从x结点开始循环，将额外的黑色结点沿着树向上移，直到：

（1）x指向一个红黑结点，此时将x单独着为黑色。

（2）x指向根，这时可以简单地消除那个额外的黑色，或者

（3）做必要的旋转和颜色改变

在循环过程中，x总是指向具有双重黑色的那个非根结点。设w是x的兄弟结点，因为x是双重黑色的，故w不可能是NIL。书中分四种情况讨论：

情况1：x的兄弟w是红色的

          此时因为x是双重黑色，贡献两个黑色结点，所有w必有黑色孩子。此时将w着为黑色，parent[x]为红色，在对parent[x]做一次左旋转。此时x的新兄弟w是黑色，这样将情况1转换为情况2、3或4。情况1的处理过程下图所示：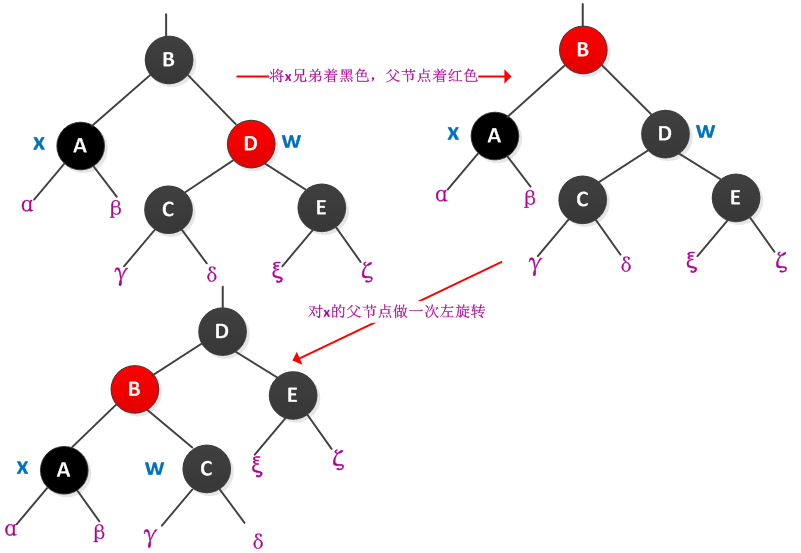

情况2：x的兄弟w是黑色的，而且w的两个孩子都是黑色的。

     处理过程是从x和w上去掉一重黑色，即x只有一重黑色而w着为红色，给x的父节点parent[x]添加额外黑色。处理过程如下图所示：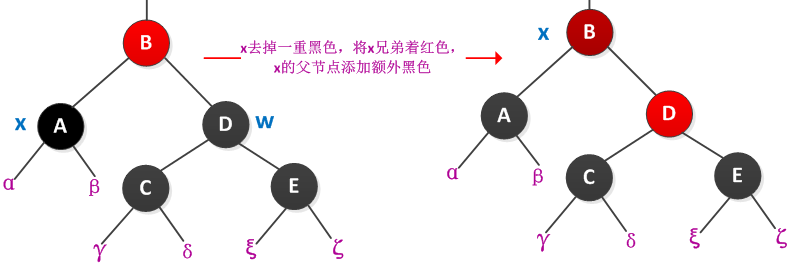

 

情况3：x的兄弟w是黑色的，w的左孩子是红色的，右孩子是黑色的

       交换w和其左孩子left[w]的颜色，并对w进行右旋转。旋转后x的新兄弟w是一个有红色右孩子的黑结点，转换成了情况4。处理过程如下图所示：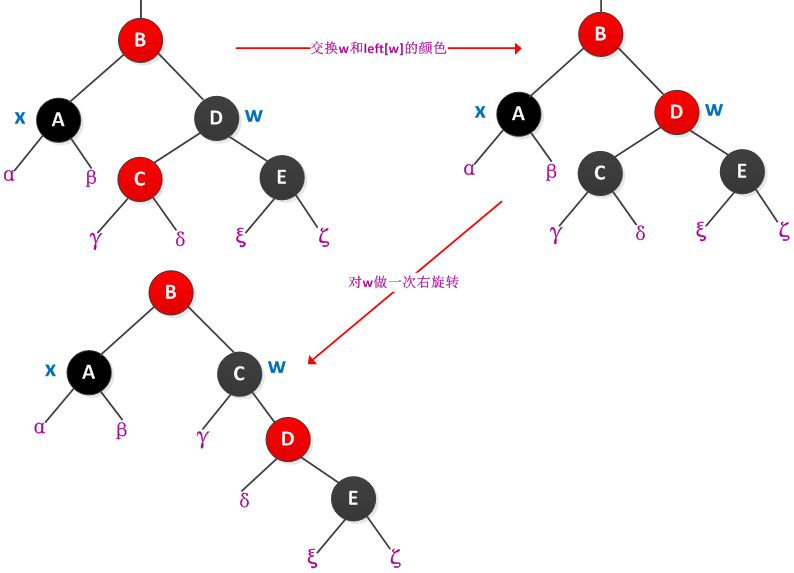

情况4：x的兄弟w是黑色的，而且w的右孩子是红色的。

　　执行过程是将w的颜色设置为parent[x]的颜色，将parent[x]的颜色设置为黑色，将w的右孩子着为黑色，然后在parent[x]做一次右旋，最后将x设置为根root。处理过程如下图所示：

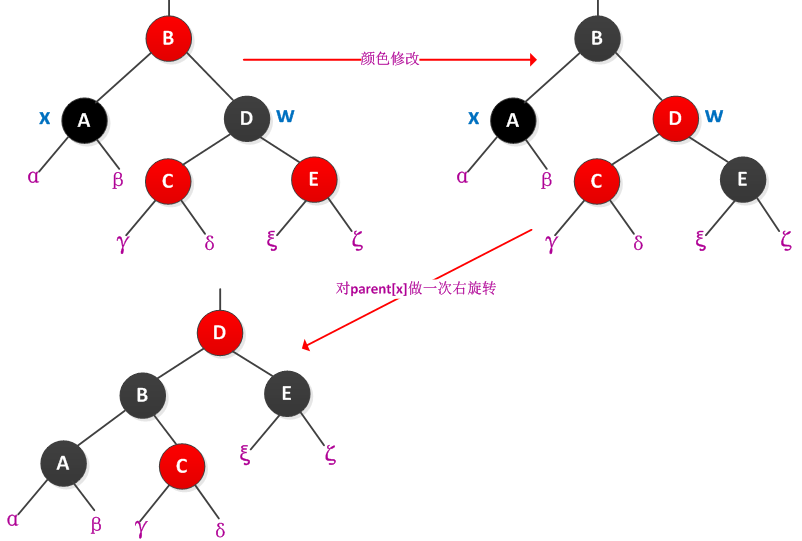
书中给出了RB_DELETE_FIXUP的伪代码：

RB_DELETE_FIXUP(T,x)
 　　while x!= root[T] and color[x] ==BLACK
         do if x == left[parent[x]]
               then w = right[parent[x]]
                    if color[w] == RED  //case 1 x的兄弟w是红色的
                       then color[w] = BLACK
                            color[parent[x]] = RED
                            LEFT_ROTATE(T,PARENT[x])
                            w = right[parent[x]]
                       if color[left[w]] == BLACK and color[right[w]] = BLACK
                       　　 then color[w] = RED  //case 2
                            x = parent[x]
                           else if color[right[w]] =BLACK
                                  then color[left[w]] = BLACK //case 3
                                       color[w] = RED
                                       RIGHT_ROTATE(T,w)
                                       w = right[parent[x]]
                               color[w] = color[parent[x]] //case 4
                               color[parent[x]] = BLACK
                               color[right[w]] = BLACK
                               LEFT_ROTATE(T,parent[x])
                               x=root(T)
             else(same as then clasue with “right” and “left” exchanged)
     color[x]=BLACK

　　

5、编程实现

　　这一章看了两天，宏观上把握了红黑树的插入和删除操作，中间还有细节问题需要思考。看完后要实现才能消化，于是我采用C++语言设计了简单的红黑树结点和红黑树类，设计的类如下所示：

static const int RED = 0;
static const int BLACK = 1;

template <class T>
class RedBlackTreeNode
{
public:
    RedBlackTreeNode():key(T()),parent(NULL),left(NULL),right(NULL),color(BLACK){}
    T key;
    RedBlackTreeNode<T>* parent;
    RedBlackTreeNode<T>* left;
    RedBlackTreeNode<T>* right;
    int color;
};

template <class T>
class RedBlackTree
{
public:
    RedBlackTree();
    int search_element(const T& k) const;
    int get_minmum(T& retmin)const;
    int get_maxmum(T& retmax)const;
    int get_successor(const T& k,T& ret) const;
    int get_predecessor(const T& k,T& ret) const;
    int insert_key(const T& k);
    int delete_key(const T& k);
    void inorder_tree_walk()const;
    RedBlackTreeNode<T>* get_root() const;
    ~RedBlackTree();
private:
    RedBlackTreeNode<T>* root;
    static  RedBlackTreeNode<T> *NIL;
    RedBlackTreeNode<T>* get_parent(RedBlackTreeNode<T>* pnode) const;
    RedBlackTreeNode<T>* get_left(RedBlackTreeNode<T>* pnode) const;
    RedBlackTreeNode<T>* get_right(RedBlackTreeNode<T>* pnode) const;
    T get_key(RedBlackTreeNode<T>* pnode) const;
    int get_color(RedBlackTreeNode<T>* pnode) const;
    void set_color(RedBlackTreeNode<T>* pnode,int color);
    void left_rotate(RedBlackTreeNode<T> *pnode);
    void right_rotate(RedBlackTreeNode<T> *pnode);
    void rb_insert_fixup(RedBlackTreeNode<T> *pnode);
    void rb_delete_fixup(RedBlackTreeNode<T> *pnode);
    RedBlackTreeNode<T>* get_maxmum(RedBlackTreeNode<T> *root) const;
    RedBlackTreeNode<T>* get_minmum(RedBlackTreeNode<T> *root) const;
    RedBlackTreeNode<T>* get_successor(RedBlackTreeNode<T> *pnode) const;
    RedBlackTreeNode<T>* get_predecessor(RedBlackTreeNode<T> *pnode) const;
    RedBlackTreeNode<T>* search_tree_node(const T& k)const;
    void make_empty(RedBlackTreeNode<T>* root);
};

　　

设计过程中采用了C++的模板类型，这样可以支持多种数据类型，使得程序具备扩展性，完整的程序实现如下所示：

#include <iostream>
#include <stack>
using namespace std;

static const int RED = 0;
static const int BLACK = 1;

template <class T>
class RedBlackTreeNode
{
public:
    RedBlackTreeNode():key(T()),parent(NULL),left(NULL),right(NULL),color(BLACK){}
    T key;
    RedBlackTreeNode<T>* parent;
    RedBlackTreeNode<T>* left;
    RedBlackTreeNode<T>* right;
    int color;
};

template <class T>
class RedBlackTree
{
public:
    RedBlackTree();
    int search_element(const T& k) const;
    int get_minmum(T& retmin)const;
    int get_maxmum(T& retmax)const;
    int get_successor(const T& k,T& ret) const;
    int get_predecessor(const T& k,T& ret) const;
    int insert_key(const T& k);
    int delete_key(const T& k);
    void inorder_tree_walk()const;
    RedBlackTreeNode<T>* get_root() const;
    ~RedBlackTree();
private:
    RedBlackTreeNode<T>* root;
    static  RedBlackTreeNode<T> *NIL;
    RedBlackTreeNode<T>* get_parent(RedBlackTreeNode<T>* pnode) const;
    RedBlackTreeNode<T>* get_left(RedBlackTreeNode<T>* pnode) const;
    RedBlackTreeNode<T>* get_right(RedBlackTreeNode<T>* pnode) const;
    T get_key(RedBlackTreeNode<T>* pnode) const;
    int get_color(RedBlackTreeNode<T>* pnode) const;
    void set_color(RedBlackTreeNode<T>* pnode,int color);
    void left_rotate(RedBlackTreeNode<T> *pnode);
    void right_rotate(RedBlackTreeNode<T> *pnode);
    void rb_insert_fixup(RedBlackTreeNode<T> *pnode);
    void rb_delete_fixup(RedBlackTreeNode<T> *pnode);
    RedBlackTreeNode<T>* get_maxmum(RedBlackTreeNode<T> *root) const;
    RedBlackTreeNode<T>* get_minmum(RedBlackTreeNode<T> *root) const;
    RedBlackTreeNode<T>* get_successor(RedBlackTreeNode<T> *pnode) const;
    RedBlackTreeNode<T>* get_predecessor(RedBlackTreeNode<T> *pnode) const;
    RedBlackTreeNode<T>* search_tree_node(const T& k)const;
    void make_empty(RedBlackTreeNode<T>* root);
};

template <class T>
RedBlackTreeNode<T>* RedBlackTree<T>::NIL = new RedBlackTreeNode<T>;

template <class T>
RedBlackTree<T>::RedBlackTree()
{
    root = NULL;
}

template <class T>
int RedBlackTree<T>::search_element(const T& k) const
{
    return (NIL != search_tree_node(k));
}

template <class T>
int RedBlackTree<T>::get_minmum(T& retmin)const
{
    if(root)
    {
        retmin = get_minmum(root)->key;
        return 0;
    }
    return -1;
}

template <class T>
int RedBlackTree<T>::get_maxmum(T& retmax)const
{
    if(root)
    {
        retmax = get_maxmum(root)->key;
        return 0;
    }
    return -1;
}

template <class T>
int RedBlackTree<T>::get_successor(const T& k,T& ret) const
{
    RedBlackTreeNode<T>* pnode = search_tree_node(k);

    if(pnode != NIL)
    {
        pnode = get_successor(pnode);
        if(pnode != NIL)
        {
            ret = pnode->key;
            return 0;
        }
        return -1;
    }
    return -1;
}
template <class T>
int RedBlackTree<T>::get_predecessor(const T& k,T& ret) const
{
    RedBlackTreeNode<T>* pnode = search_tree_node(k);
    if(pnode != NIL)
    {
        pnode = get_predecessor(pnode);
        if(pnode != NIL)
        {
            ret = pnode->key;
            return 0;
        }
        return -1;
    }
    return -1;
}

template <class T>
int RedBlackTree<T>::insert_key(const T& k)
{
    RedBlackTreeNode<T> *newnode = new RedBlackTreeNode<T>;
    newnode->key = k;
    newnode->color = RED;
    newnode->left = NIL;
    newnode->right = NIL;
    newnode->parent = NIL;

    if(NULL == root)
        root = newnode;
    else
    {
        RedBlackTreeNode<T>* pnode = root;
        RedBlackTreeNode<T>* qnode;
        while(pnode != NIL)
        {
            qnode = pnode;
            if(pnode->key > newnode->key)
                pnode = pnode->left;
            else
                pnode = pnode->right;
        }
        newnode->parent = qnode;
        if(qnode->key > newnode->key)
            qnode->left = newnode;
        else
            qnode->right = newnode;
    }
    rb_insert_fixup(newnode);
    return 0;
}

template <class T>
int RedBlackTree<T>::delete_key(const T& k)
{
     RedBlackTreeNode<T>* pnode = search_tree_node(k);
    if(NIL != pnode)
    {
        RedBlackTreeNode<T>* qnode,*tnode;
        if(get_left(pnode) == NIL || get_right(pnode) == NIL)
            qnode = pnode;
        else
            qnode = get_successor(pnode);
        if(get_left(qnode) != NIL)
            tnode = get_left(qnode);
        else
            tnode = get_right(qnode);
        tnode->parent = get_parent(qnode);
        if(get_parent(qnode) == NIL)
            root = tnode;
        else if(qnode == get_left(get_parent(qnode)))
            qnode->parent->left = tnode;
        else
            qnode->parent->right = tnode;
        if(qnode != pnode)
             pnode->key = get_key(qnode);
        if(get_color(qnode) == BLACK)
            rb_delete_fixup(tnode);
        delete qnode;
        return 0;
    }
    return -1;
}

template <class T>
RedBlackTree<T>::~RedBlackTree()
{
    make_empty(root);
}
template <class T>
RedBlackTreeNode<T>* RedBlackTree<T>:: get_root() const
{
    return root;
}
template <class T>
RedBlackTreeNode<T>* RedBlackTree<T>::get_parent(RedBlackTreeNode<T>* pnode) const
{
    return pnode->parent;
}
template <class T>
RedBlackTreeNode<T>* RedBlackTree<T>::get_left(RedBlackTreeNode<T>* pnode) const
{
    return pnode->left;
}
template <class T>
RedBlackTreeNode<T>* RedBlackTree<T>::get_right(RedBlackTreeNode<T>* pnode) const
{
    return pnode->right;
}
template <class T>
T RedBlackTree<T>::get_key(RedBlackTreeNode<T>* pnode) const
{
    return pnode->key;
}
template <class T>
int RedBlackTree<T>::get_color(RedBlackTreeNode<T>* pnode) const
{
    return pnode->color;
}

template <class T>
void RedBlackTree<T>::set_color(RedBlackTreeNode<T>* pnode,int color)
{
    pnode->color = color;
}

template <class T>
void RedBlackTree<T>::left_rotate(RedBlackTreeNode<T> *pnode)
{
    RedBlackTreeNode<T>* rightnode = pnode->right;
    pnode->right = rightnode->left;
    if(rightnode->left != NIL)
        rightnode->left->parent = pnode;
    rightnode->parent = pnode->parent;
    if(pnode->parent == NIL)
        root = rightnode;
    else if(pnode == pnode->parent->left)
        pnode->parent->left = rightnode;
    else
        pnode->parent->right = rightnode;
    rightnode->left = pnode;
    pnode->parent = rightnode;
}

template <class T>
void RedBlackTree<T>::right_rotate(RedBlackTreeNode<T> *pnode)
{
    RedBlackTreeNode<T>* leftnode = pnode->left;
    pnode->left = leftnode->right;
    if(leftnode->right != NIL)
        leftnode->right->parent = pnode;
    leftnode->parent = pnode->parent;
    if(pnode->parent == NIL)
        root = leftnode;
    else if(pnode == pnode->parent->left)
        pnode->parent->left = leftnode;
    else
        pnode->parent->right = leftnode;
    leftnode->right = pnode;
    pnode->parent = leftnode;
}
template <class T>
void RedBlackTree<T>::rb_insert_fixup(RedBlackTreeNode<T>*pnode)
{
    RedBlackTreeNode<T> *qnode,*tnode;
    //当pnode的父节点为红色时，破坏性质4
    while(get_color(get_parent(pnode))== RED)
    {
        qnode = get_parent(get_parent(pnode));//祖父结点
        if(get_parent(pnode) == get_left(qnode))
        {
            tnode = get_right(qnode);//pnode的叔叔结点
            if(get_color(tnode) == RED) //case1 叔叔结点为红色
            {
                set_color(get_parent(pnode),BLACK);
                set_color(tnode,BLACK);
                set_color(qnode,RED);
                pnode = qnode;
            }
            else  //case 2 or case 3
            {
                if(pnode == get_right(get_parent(pnode)))  //case2 pnode为右孩子
                {
                    pnode = get_parent(pnode);
                    left_rotate(pnode);
                }
                //case3 pnode为左孩子
                set_color(get_parent(pnode),BLACK);
                qnode = get_parent(get_parent(pnode));
                set_color(qnode,RED);
                right_rotate(qnode);
            }
        }
        else
        {
            tnode = get_left(qnode);
            if(get_color(tnode) == RED)
            {
                set_color(get_parent(pnode),BLACK);
                set_color(tnode,BLACK);
                set_color(qnode,RED);
                pnode = qnode;
            }
            else
            {
                if(pnode == get_left(get_parent(pnode)))
                {
                    pnode = get_parent(pnode);
                    right_rotate(pnode);
                }
                set_color(get_parent(pnode),BLACK);
                qnode = get_parent(get_parent(pnode));
                set_color(qnode,RED);
                left_rotate(qnode);
            }
        }
    }
    set_color(root,BLACK);
}

template <class T>
void RedBlackTree<T>::rb_delete_fixup(RedBlackTreeNode<T> *pnode)
{
    while(pnode != root && get_color(pnode) == BLACK)
    {
        RedBlackTreeNode<T> *qnode,*tnode;
        if(pnode == get_left(get_parent(pnode)))
        {
            qnode = get_right(get_parent(pnode));
            if(get_color(qnode) == RED)
            {
                set_color(qnode,BLACK);
                set_color(get_parent(pnode),RED);
                left_rotate(get_parent(pnode));
                qnode = get_right(get_parent(pnode));
            }
            if(get_color(get_left(qnode)) == BLACK && get_color(get_right(qnode)) == BLACK)
            {
                set_color(qnode,RED);
                pnode = get_parent(pnode);
            }
            else
            {
                if(get_color(get_right(qnode)) == BLACK)
                {
                    set_color(get_left(qnode),BLACK);
                    set_color(qnode,RED);
                    right_rotate(qnode);
                    qnode = get_right(get_parent(pnode));
                }
                set_color(qnode,get_color(get_parent(pnode)));
                set_color(get_parent(pnode),BLACK);
                set_color(get_right(qnode),BLACK);
                left_rotate(get_parent(pnode));
                pnode = root;
            }
        }
        else
        {
            qnode = get_left(get_parent(pnode));
            if(get_color(qnode) == RED)
            {
                set_color(qnode,BLACK);
                set_color(get_parent(pnode),RED);
                right_rotate(get_parent(pnode));
                qnode = get_left(get_parent(pnode));
            }
            if(get_color(get_right(qnode)) == BLACK && get_color(get_left(qnode)) == BLACK)
            {
                set_color(qnode,RED);
                pnode = get_parent(pnode);
            }
            else
            {
                if(get_color(get_left(qnode)) == BLACK)
                {
                    set_color(get_right(qnode),BLACK);
                    set_color(qnode,RED);
                    left_rotate(qnode);
                    qnode = get_left(get_parent(pnode));
                }
                set_color(qnode,get_color(get_parent(pnode)));
                set_color(get_parent(pnode),BLACK);
                set_color(get_left(qnode),BLACK);
                right_rotate(get_parent(pnode));
                pnode = root;
            }
        }
    }
    set_color(pnode,BLACK);
}

template <class T>
RedBlackTreeNode<T>* RedBlackTree<T>::get_maxmum(RedBlackTreeNode<T> *root) const
{
    RedBlackTreeNode<T> *pnode = root;
    while(pnode->right != NIL)
        pnode = pnode->right;
    return pnode;
}

template <class T>
RedBlackTreeNode<T>* RedBlackTree<T>::get_minmum(RedBlackTreeNode<T> *root) const
{
    RedBlackTreeNode<T> *pnode = root;
    while(pnode->left != NIL)
        pnode = pnode->left;
    return pnode;
}

template <class T>
RedBlackTreeNode<T>* RedBlackTree<T>:: get_successor(RedBlackTreeNode<T> *pnode) const
{
    if(pnode->right != NIL)
        return get_minmum(pnode->right);
    RedBlackTreeNode<T>* parentnode = get_parent(pnode);
    while(parentnode != NIL && get_right(parentnode) == pnode)
    {
            pnode = parentnode;
            parentnode = get_parent(pnode);
    }
    return parentnode;
}

template <class T>
RedBlackTreeNode<T>* RedBlackTree<T>::get_predecessor(RedBlackTreeNode<T> *pnode) const
{
    if(pnode->left != NIL)
        return get_maxmum(pnode->left);
    RedBlackTreeNode<T>* parentnode = get_parent(pnode);
    while(parentnode != NIL && get_left(parentnode) == pnode)
    {
        pnode = parentnode;
        parentnode = get_parent(pnode);
    }
    return parentnode;
}

template <class T>
RedBlackTreeNode<T>* RedBlackTree<T>:: search_tree_node(const T& k)const
{
    RedBlackTreeNode<T>* pnode = root;
    while(pnode != NIL)
    {
        if(pnode->key == k)
            break;
        else if(pnode->key > k)
            pnode = pnode->left;
        else
            pnode = pnode->right;
    }
    return pnode;
}

template <class T>
void RedBlackTree<T>::make_empty(RedBlackTreeNode<T>* root)
{
    if(root)
    {
        RedBlackTreeNode<T> *pleft = root->left;
        RedBlackTreeNode<T>* pright = root->right;
        delete root;
        if(pleft != NIL)
            make_empty(pleft);
        if(pright != NIL)
            make_empty(pright);
    }
}
template <class T>
void RedBlackTree<T>::inorder_tree_walk()const
{
    if(NULL != root)
     {
         stack<RedBlackTreeNode<T>* > s;
         RedBlackTreeNode<T> *ptmpnode;
         ptmpnode = root;
         while(NIL != ptmpnode || !s.empty())
         {
             if(NIL != ptmpnode)
             {
                 s.push(ptmpnode);
                 ptmpnode = ptmpnode->left;
             }
             else
             {
                 ptmpnode = s.top();
                 s.pop();
                 cout<<ptmpnode->key<<":";
                 if(ptmpnode->color == BLACK)
                    cout<<"Black"<<endl;
                 else
                    cout<<"Red"<<endl;
                 ptmpnode = ptmpnode->right;
             }
         }
     }
}
int main()
{
    RedBlackTree<int> rbtree;
    int value;
    rbtree.insert_key(41);
    rbtree.insert_key(38);
    rbtree.insert_key(31);
    rbtree.insert_key(12);
    rbtree.insert_key(19);
    rbtree.insert_key(8);
    cout<<"root is: "<<rbtree.get_root()->key<<endl;
    cout<<"Inorder walk red black tree:"<<endl;
    rbtree.inorder_tree_walk();
    if(rbtree.get_minmum(value) == 0)
        cout<<"minmum is: "<<value<<endl;
    if(rbtree.get_maxmum(value) == 0)
        cout<<"maxmum is: "<<value<<endl;
    if(rbtree.get_successor(19,value) == 0)
        cout<<"19 successor is: "<<value<<endl;
    if(rbtree.get_predecessor(19,value) == 0)
        cout<<"19 predecessor is: "<<value<<endl;
    if(rbtree.delete_key(38)==0)
        cout<<"delete 38 successfully"<<endl;
    cout<<"root is: "<<rbtree.get_root()->key<<endl;
    cout<<"Inorder walk red black tree:"<<endl;
    rbtree.inorder_tree_walk();
    return 0;
}

程序测试结果如下所示：

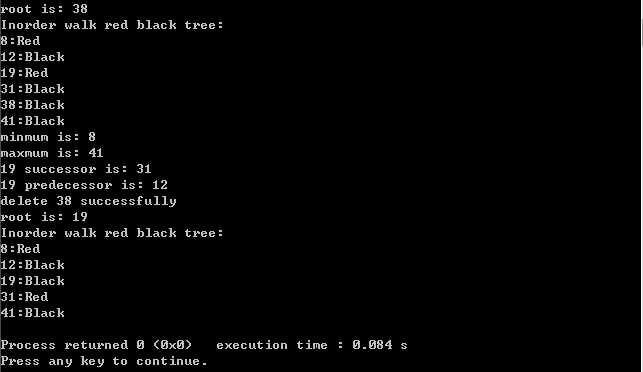
　　实现过程中感触非常多，需要很大的耐心去调试程序，关键的是insert和delete操作。

第十四章：数据结构的扩张

前言：通常我们会遇到一些问题，采用一些标准的数据结构，如双链表、散列表或二叉查找数时，不能够满足操作要求，需要对这些数据结构进行扩张，添加一些额外的信息使得能够完成新的操作。附加的信息需要对数据结构的某些操作进行调整，这个是非常关键的步骤，决定着数据结构扩张是否能够实现。本章主要讨论了红黑树结构的扩张，介绍了两种扩张方式。第一种方式扩张使得红黑色能够支持动态集合上顺序统计，快速找出集合中第i小的数，或给出某个元素在集合的全序中的排名。第二种方式扩张使得红黑色能够进行区间操作，可以很快地找到集合中覆盖的区间。关于红黑色请参考第13章，http://www.cnblogs.com/Anker/archive/2013/01/30/2882773.html。

1、动态顺序统计

　　在第九章介绍了顺序统计的概念，大概的意思是在包含有n个元素的集合中，第i个顺序统计量指的是该集合中第i小的元素。在一个无序的集合中，任意顺序统计量都可以在O(n)时间内找到，详细情况可以参考http://www.cnblogs.com/Anker/archive/2013/01/25/2877311.html。书中在此基础上修改红黑树的结构，使得任意的顺序统计量都可以再O(lgn)时间内确定。向红黑树的结构中添加一个size域，表示包含自身节点的当前节点的子树节点的数目。这样修改后可以快速支持顺序统计量操作，将这种修改后的红黑树叫做：顺序统计量树T。修改后的结构如下所示：

struct RBTreeNode
{
   int key;
   int color;
   struct RBTreeNode *parent;
   struct RBTreeNode *left;
   struct RBTreeNode *right;
   int size;  
};

例如给定红黑树的一个节点x，则size[x] = size[left[x]]+size[right[x]]+1。size[x]为包含以x为根的子树的节点数（包含x本身），即子树的大小。如果哨兵定义为0，即设置size[nil[T]]=0。

下面给出一个修改后的红黑树的例子，如下图所示：

　　红黑树是二叉排序树，按照中序遍历从小到大输出红黑树中的关键字。从图中可以看出，添加size域后，很方便看出每个节点的子树的节点数目（包含自身节点）。书中在后面讨论这种结构的操作，分别讨论如下：

（1）检索具有给定排序的元素

　　过程OS_SELECT(x,i)返回一个指向以x为根的子树中包含第小关键字的结点的指针，即为了找出顺序统计量树T中的第i小关键字，可以调用OS_SELECT(root[T],i)。书中给出了伪代码如下：

OS_SELECT(x,i)
    r = size[left[x]]+1; //先计算x的处于的位置
    if i = r         //x正好是第i小的关键字
        then return x;   else if i < r   //x比第i关键字大，则在其左子树查找
        then return OS_SELECT(left[x],i)
    else return OS_SELECT(right[x],i-r)  //x比第i关键字小，则在其右子树查找

　　该过程类似二分查找，每一次递归调用都在顺序统计数中下降一层，故最坏情况下OS_SELECT的总时间与树的高度成正比，红黑树的高度为lgn。故OS_SELECT的运行时间为：O(lgn)。

（2）确定一个元素的秩（位置）

　　给定指向一顺序统计树T中节点x的指针，求x在顺序统计树中序遍历得到的线性序中的位置。书中给出了OS_RANK(T,x)过程的伪代码：

OS_RANK(T,x)
    r = size[left[x]]+1;   //获取以x为根子树中x的位置（中序遍历）
    y = x;
    while y != root[T]    //从下向上直到根节点
          do if y = right[p[y]]   //如果是右子树
                 then  r = r + size[left[p[y]]]+1; 
          y = p[y]; //向上移动
    return r;

　　从程序总可以看出当y == root[T]时候循环终止，此时以y为根的子树是课完整树，此时r值是这颗整树中key[x]的秩。while循环中的每一次迭代花O(1)时间，且y在每次迭代中沿树上升一层，故在最坏情况下0S_RANK的运行时间与树的高度成正比：对含n个节点的顺序统计树时间为O(lgn)。

（3）对子树规模的维护

　　在红黑树中添加size域后，能够通过OS_SELECT和OS_RANK迅速计算出所需的顺序统信息。通过修改红黑树的插入和删除操作，在此过程是通过旋转来修改size域。关于这部分需要在红黑树的基础上进行改进，比较复杂，暂时没有实现。

2、如何扩张数据结构

对一种数据结构的扩张过程分为四个步骤：

1）选择基础数据结构

2）确定要在基础数据结构中添加哪些信息

3）验证可用基础数据结构上的基本修改操作来维护这些新添加的信息

4）设计新的操作

　　书中给出了对红黑树进行扩张的定理，并给出了证明，这个看的时候有些难度，暂时跳过了。大概意思就是说当红黑树被选作基础数据结构时，某些类型的附加信息总是可以用插入和删除来进行有效地维护。

3、区间树

　　这小结讲的是扩张红黑树以支持由区间构成的动态集合上的操作。区间可以很方便的表示各占用一段连续时间的一些事情。区间树是一种动态集合进行维护的红黑树，该集合中的每个元素x都包含在一个区间int[x]。区间树支持下列操作：

INTERVAL_INSERT(T,x)：将包含区间域int的元素x插入到区间树T中

INTERVAL_DELETE(T,X)：从区间树T中删除元素x

INTERVAL_SEARCH(T,i)：返回一个指向区间树T中元素x的指针，使int[x]与i重叠，若集合中无此元素存在，则返回nil[T]。

修改红黑树得到的区间树如下图所示：

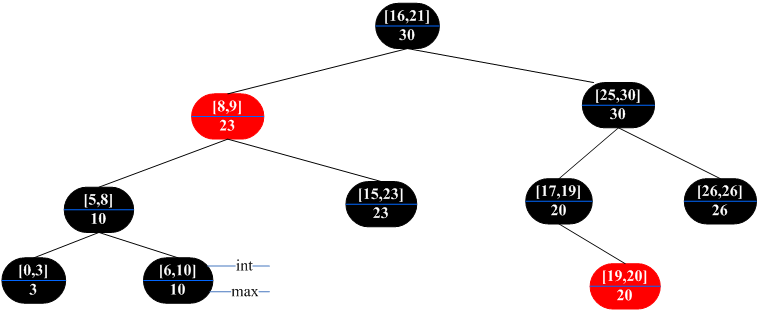
从图可以看出，对区间树以每个节点的左端点值进行中序变量即可得到有序的序列。有了区间树的结果就很容易实现其相关操作。

4、总结

　　本章主要是介绍一种数据结构扩张的方法，灵活性非常之大。以红黑树作为例子，我是在年前看的红黑树，并给以实现。年后了，对红黑树忘了差不多了。呵呵，真是一天不学习，赶不上啦。本章看完比较郁闷，没有去实现。实现的难度非常具有挑战性，何时能够实现，我心里有些忐忑。肯定不会放弃，一定会找个时间把这些实现一下。