[CF1149C](Tree Generator)

• 题意

给出一颗树的括号序，有m个操作，每次交换两个括号，保证交换后括号序仍然合法，输出每次操作后（包括未操作时）树的直径

• solution

首先转化题目，对于一棵树的括号序，我们找到一段子串，满足将其中匹配的括号消去后剩下的括号最多，那么剩下的括号个数即为所求直径

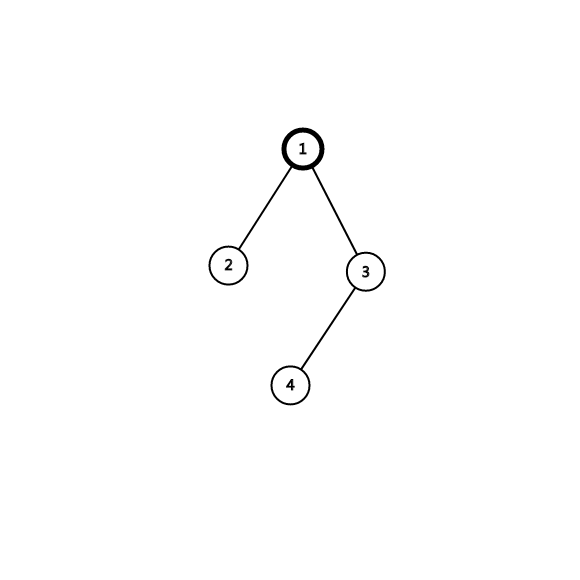
这样一棵树括号序为()(()) 取出)((，消去匹配括号后剩下3个括号，为所求直径

但这样还是不可做nya，于是我们再转化，钦定左括号值为1，右括号值为-1，问题变为找到相邻的两段，使后一段的数字和减前一段的数字和最大，这个差就是答案

想到这里你就能切这题

那么问题已经转化到这么可做了，对于一个区间问题+待修+维护一些有关区间的值，我们可以用线段树这种简单（奥妙重重）的数据结构

对于每个线段树节点，我们维护 前/后 最小/大值，区间和，答案以及所有 前/后 缀D值的最大值区间D值

D值是什么呢？我们简单为在指定区间内划一条分界线，使 后一半和 减 前一半和 最大，这个差就是这个区间的D值

• code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#define ls (x<<1)
#define  rs (x<<1|1)
#define mid ((l+r)>>1)
#define N 200000
using namespace std;
struct zero{
int sum,prex,prem,sucx,sucm,pred,sucd,d,ans;
zero(){}
zero(int p1,int p2,int p3,int p4,int p5,int p6,int p7,int p8,int p9){sum=p1,prex=p2,prem=p3,sucx=p4,sucm=p5,pred=p6,sucd=p7,d=p8,ans=p9;}
}tree[N<<2];
// sum:区间和
// ans:区间答案
// pre/suc-x/m 区间 前/后 缀最 大/小 值
// pre/suc-d 前/后 缀 D值
// d 区间D 值 
const zero L=zero(1,1,0,1,0,1,1,1,1);
const zero R=zero(-1,0,-1,0,-1,1,1,1,1);
char input[N];
zero operator +(const zero &a,const zero &b){
    zero c;
    c.prex=max(a.prex,a.sum+b.prex);
    c.sucx=max(b.sucx,a.sucx+b.sum);
    c.prem=min(a.prem,a.sum+b.prem);
    c.sucm=min(b.sucm,a.sucm+b.sum);
    c.d=max(b.d-a.sum,a.d+b.sum);
    c.pred=max(a.pred,max(b.pred-a.sum,a.d+b.prex));
    c.sucd=max(b.sucd,max(b.sum+a.sucd,b.d-a.sucm));
    c.sum=a.sum+b.sum;
    c.ans=max(max(a.ans,b.ans),max(b.pred-a.sucm,a.sucd+b.prex));
    return c;
}
void build(int x,int l,int r){
    if(l==r){if(input[l]=='(')tree[x]=L;else tree[x]=R;return;}
    build(ls,l,mid),build(rs,mid+1,r);
    tree[x]=tree[ls]+tree[rs];
}
void update(int x,int l,int r,int pos){
    if(l==r){if(input[l]=='(')tree[x]=L;else tree[x]=R;return;}
    if(pos<=mid)update(ls,l,mid,pos);else update(rs,mid+1,r,pos);
    tree[x]=tree[ls]+tree[rs];
}
int n,m;
int main(){
    scanf("%d%d",&n,&m);n=(n-1)*2;
    scanf("%s",input+1);
    build(1,1,n);
    printf("%d\n",tree[1].ans);
    for(int i=1;i<=m;i++){
        int a,b;
        scanf("%d%d",&a,&b);
        swap(input[a],input[b]);
        update(1,1,n,a),update(1,1,n,b);
        printf("%d\n",tree[1].ans);
    }
}