2020杭电多校 4G / HDU 6808 - Go Running (二分图最小顶点覆盖/离散化)
题意
有一条路可以看成是无尽头的数轴
学生可以选择一个点开始跑步,可以选择从任意时间\(t_1\)开始跑,从任意时间\(t_2\)结束跑步,也可以选择跑步方向,但跑步速度恒定为\(1\ m/s\)
跑步开始前不会出现在数轴上,跑步结束后也不会出现在数轴上
这条路上有一些监控,你收到了\(n\)份报告,每份报告有两个数据\(x_i\)和\(t_i\),表示时间为\(t_i\)秒时在数轴的\(x_i\)位置有至少一个学生在跑步
问最少有多少个学生在跑步
思路
谁知道\(O(n^2m)\)的Dinic能在\(T_{max}=100,\ n_{max}=10^5\)的题里跑这么快?
完全不用考虑数据范围,直接当二分图最小顶点覆盖/二分图最大匹配模板题做
可以忽视题目中”跑步开始前不会出现在数轴上,跑步结束后也不会出现在数轴上“这句话
因为即使出现在数轴上,没被监控拍到报告也就对题目无影响
而如果被监控拍到,那么就可以把符合他的跑步条件的所有报告全部看成只有他一个人在跑步(最优)使得总人数理论最少
假设某份报告表示\(t_i\)时刻在\(x_i\)位置有人跑步
那么这个人就当他至始至终都在跑步,那么有以下两种可能:
一、他从\(x_i-t_i\)位置开始跑步,向数轴正方向跑
二、他从\(x_i+t_i\)位置开始跑步,向数轴负方向跑
那么对于这两种情况,在\(xOt\)坐标系内,就相当于根据一个点\((x_i,t_i)\)画出了两条斜率分别为\(1\)和\(-1\)的直线
如下图,如果\((x_i,t_i)\)对应\((2,2)\),则可以在\(xOt\)平面内画出可能的两条运动轨迹函数

对于题目中的样例一,绘图如下
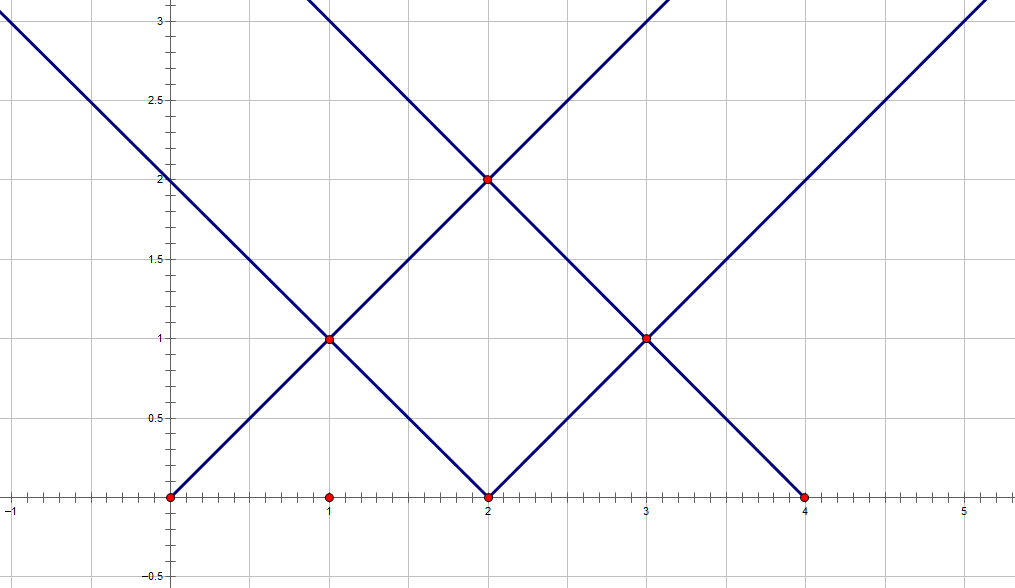
所以此时题目就转变成了:选择最少的直线,能够包括所有给定的点\((x_i,t_i)\)
发现就是一道二分图最小顶点覆盖的模板题
可以将斜率为\(1\)和\(-1\)的两类曲线当作二分图中\(U\)集和\(V\)集,如果存在某个点\((x_i,t_i)\),则将\(x_i-t_i\)放入\(U\)集,将\(x_i+t_i\)放入\(V\)集,并在两者之间连一条边
如果选择了某个点,就把所有与其相邻的边从图中去掉,所以求的就是最小顶点覆盖
完整程序
下面直接使用dinic跑二分图最小顶点覆盖
建图为:
原点连向所有形如\(x_i-t_i\)的点,流量为1
所有形如\(x_i-t_i\)的点连向汇点,流量为1
所有形如\(x_i-t_i\)的点连向形如\(x_i-t_i\)的点,流量为\(\infin\)
由于数据达\(10^9\),需要先离散化
同理使用其余解决二分图最小顶点覆盖/二分图最大匹配的算法基本都能过(例如匈牙利)
未了解过二分图的可以瞅瞅【图论】二分图/二分图最大匹配/二分图最大权完美匹配呀
(2386ms/5000ms)
#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=333333,maxm=666666;
struct edge{
int u,v,cap,flow;
edge(){}
edge(int u,int v,int cap,int flow):u(u),v(v),cap(cap),flow(flow){}
}eg[maxm<<1];
int tot,s,t,dis[maxn<<1],cur[maxn<<1];
vector<int> tab[maxn<<1];
void init(int n,int s_,int t_){
while(n)tab[n--].clear();
tot=0,s=s_,t=t_;
}
void addedge(int u,int v,int cap){
tab[u].push_back(tot);
eg[tot++]=edge(u,v,cap,0);
tab[v].push_back(tot);
eg[tot++]=edge(v,u,0,0);
}
int bfs(){
queue<int> q;
q.push(s);
memset(dis,INF,sizeof dis);
dis[s]=0;
while(!q.empty()){
int h=q.front(),i;
q.pop();
for(i=0;i<tab[h].size();i++){
edge &e=eg[tab[h][i]];
if(e.cap>e.flow&&dis[e.v]==INF){
dis[e.v]=dis[h]+1;
q.push(e.v);
}
}
}
return dis[t]<INF;
}
int dfs(int x,int maxflow){
if(x==t|maxflow==0)
return maxflow;
int flow=0,i,f;
for(i=cur[x];i<tab[x].size();i++){
cur[x]=i;
edge &e=eg[tab[x][i]];
if(dis[e.v]==dis[x]+1&&(f=dfs(e.v,min(maxflow,e.cap-e.flow)))>0){
e.flow+=f;
eg[tab[x][i]^1].flow-=f;
flow+=f;
maxflow-=f;
if(maxflow==0)
break;
}
}
return flow;
}
int dinic(){
int flow=0;
while(bfs()){
memset(cur,0,sizeof(cur));
flow+=dfs(s,INF);
}
return flow;
}
int ar[222222],cnt;
int X[111111],T[111111];
void solve()
{
int n;
cin>>n;
cnt=0;
for(int i=1;i<=n;i++)
{
cin>>T[i]>>X[i];
ar[++cnt]=X[i]-T[i];
ar[++cnt]=X[i]+T[i];
}
sort(ar+1,ar+1+cnt);
cnt=unique(ar+1,ar+1+cnt)-ar-1;
init(2*cnt+2,2*cnt+1,2*cnt+2);
for(int i=1;i<=n;i++)
{
int a=lower_bound(ar+1,ar+1+cnt,X[i]-T[i])-ar;
int b=lower_bound(ar+1,ar+1+cnt,X[i]+T[i])-ar;
addedge(a,b+cnt,INF);
}
for(int i=1;i<=cnt;i++)
addedge(s,i,1),addedge(i+cnt,t,1);
cout<<dinic()<<'\n';
}
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
int T;cin>>T;
while(T--)
solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号