OO第一单元总结

OO第一单元总结

（一）基于度量的程序结构分析

第一次作业

方法复杂度

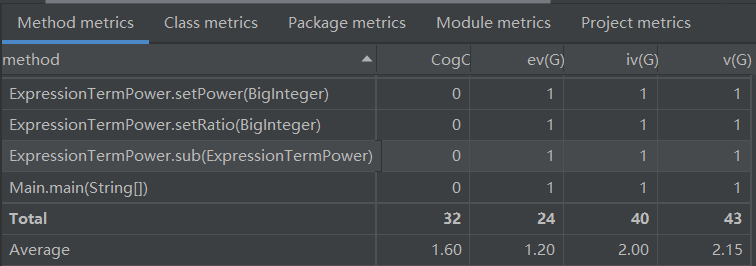
因为第一次作业比较简单，因此代码维护难度，模块耦合程度，测试和维护难度指数均不是很高，第一次面向对象的作业主要理解了面向对象的编程思想，和之前面向过程的编程有一定的差别。

类复杂度分析

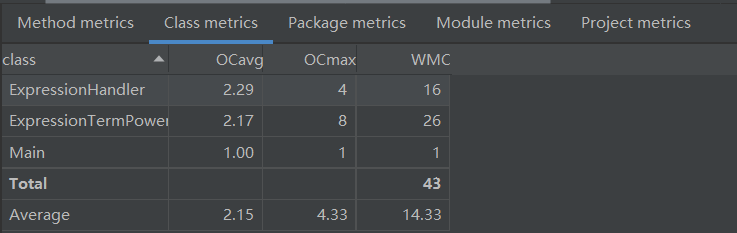
没有出现红色字体的提示，整体的复杂度不高

整体代码量

uml类图

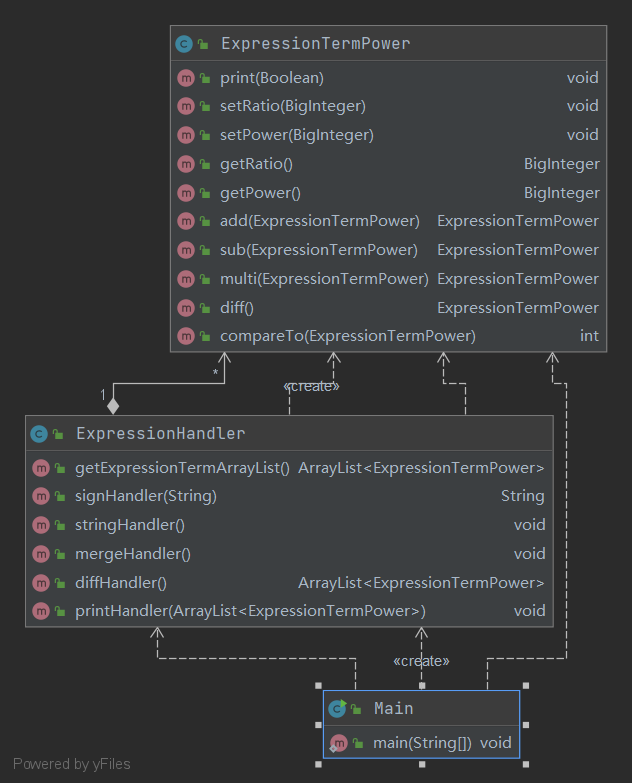
类的设计思路

本次作业因为只有多项式，也没有过多的考虑扩展性，因此只有三个类，也没有什么继承，其中ExpressionTermPower 是多项式类，用系数和指数来构造一个多项式项，ExpressionHandler用于处理表达式，其中使用了正则替换也就是删除空格和\t,连续的+/-替换成一个+/-，为了让项的格式统一，在第一个项之前没有符号的时候补上一个+

优缺点分析

• 优点：

基本采用面向对象的思想，明显体会到面向对象编程可以有更好的视野，对程序结构了解更清晰

• 缺点：

1.因为IDEA生成get(),set()方法非常方便，因此第一次作业中为所有变量都设计了get(),set()方法，但是有一些方法并没有被用到，因此造成了代码的冗余

2.没有使用继承，可扩展性差，第二次作业基本完全重构

第二次作业

方法复杂度

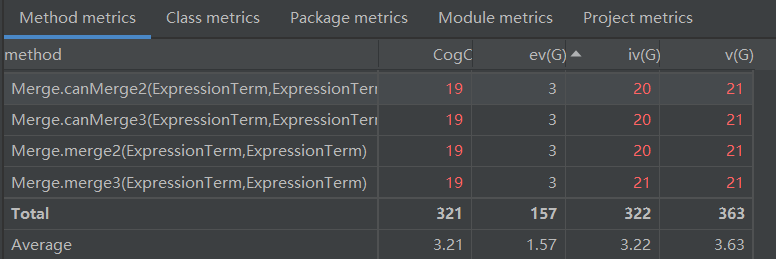
因为方法过多因此只截图显示出现红色警告字体的部分，相比第一次作业，第二次作业出现了一些方法的耦合性较高，测试和维护难度较高，（相对应的系数也有明显的增大）这在debug过程中也有感觉，在单步调试中，会调用很多类的不同方法难以判断是哪个方法出现了问题导致了bug

类复杂度

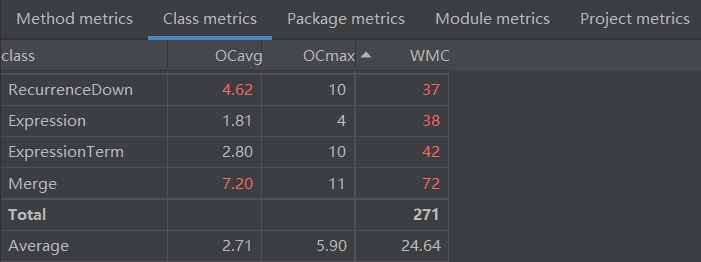
因为类较多，因此截图显示出现红色警告字体的部分 ，复杂度较高的类主要是递归下降，表达式合并表达式，表达式项的类。

整体代码量

代码量最大的几个类也是复杂度最高的那几个类，个人感觉对于较大的类的处理不太好，或者以后可以考虑尽量不出现较大的类，可以降低耦合度，让程序更便于调试

uml类图

类的设计思路

• RecurrenceDown

  递归下降解析表达式，但是并没有完全使用递归下降，而是分析到表达式因子这一级的时候采用小正则来解析表达式，一方面是因为最开始我并没有写这个类，而是在表达式类中有一个解析的方法，递归的调用项的解析方法，在项的解析方法中调用了因子的解析方法，在因子中使用小正则表达式，后面了解到这是递归下降的思想，因此才写了这个类，同时把解析过程放进了这个类，也没有改为纯粹的递归下降，而是递归+正则的方法，另一方面是第二次加入了表达式因子让我需要重构，重构过程中感觉这样写更加合适

• Splite

  在本次作业中，可能有括号的存在，根据表达式文法，可能存在很深的嵌套，为了防止计算过慢，选择了在开始的时候拆分所有的括号，同时处理冗余的括号，同时，拆括号还可能带来一些化简，比如(x+sin(x))*sin(x) + cos(x) ** 2在拆掉括号之后可以化简为xsin(x)，经过分析，拆括号带来的缩短表达式长度的收益有时为正有时为负，但个人认为为正或者很小的负收益的情况较多，因此不做判断直接拆掉所有括号

• Merge

  用于表达式合并同类项，其中主要考虑了三种化简方式，

  1.两个项除系数外完全相同，可以直接合并

  2.两个项提公因式提出相同项后，一个剩余sin(x)**2，一个剩余cos(x)**2且符号相同，可以化简为公因式

  3.两个项提公因式提出相同项后，一个剩余sin(x)**2，一个剩余cos(x)**2且符号相反，可以化简为公因式*(2*cos(x)-1)

• 表达式各等级对应的类

  第二次作业中，表达式的等级划分为了表达式，表达式项，表达式因子，在设计中把常数因子看作了幂次为0的幂函数因子设计了三种因子类：幂函数，三角函数，表达式因子，都继承了公共的父类Factor，定义了三角函数类型的枚举型，包含sin和cos，对每个项，合并所有的幂函数因子和sin，cos因子，加入项的因子容器中，其中幂函数因子放在最后，表达式的每个等级的类中，都加入了相应的求导方法，采用了课程组给出的求导公式。

优点和缺点

• 优点：

1.个人认为优化做的还算不错，最终的性能分整体也不错，也考虑到了括号引起递归求导超时的可能性

2.采用了继承，虽然代码的复杂度有明显提升，但是整体的可读性还不错

• 缺点：

1.有几个类和一些方法写的太长，其中也有不少重复的部分，代码重复度高的地方应该可以优化的，但是没有想到很好的方法去做，代码整体的耦合度和维护难度较高

2.依旧采用了正则表达式替换空格，\t和连续的加减号，不利于加入判断格式正确性这一功能

3.优化方法的一个小问题，当出现sin(x)或者cos(x)的负次幂的时候，会去凑出一个sin(x)**2和cos(x)**2从而导致产生负收益的优化

第三次作业

方法复杂度

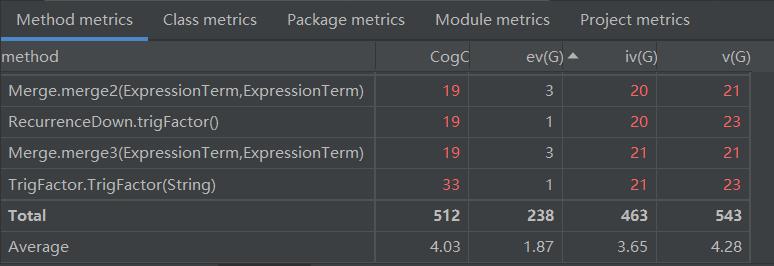
依然存在一些方法的复杂度较高，和上次作业相同，复杂度较高的几个方法是合并方法，整体的耦合度和调试难度又有了一点上升，但可读性还算不错

类复杂度

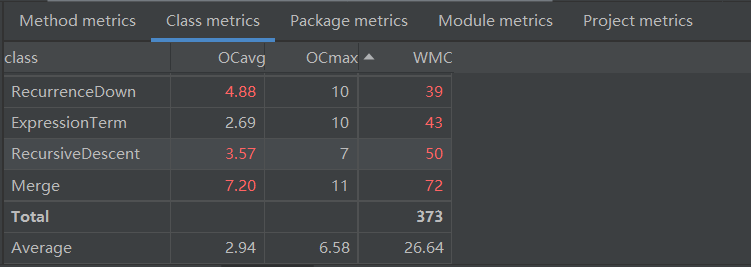
复杂度最高的类是两个递归下降类，一个用于判断表达式是否格式正确，一个用于解析表达式（这个类和上次作业完全一样），然后就是合并和表达式项的类，整体的平均复杂度也有一点上升。

整体代码量

和上次作业一样，代码量最大的几个类也是复杂度最高的那几个类

uml类图

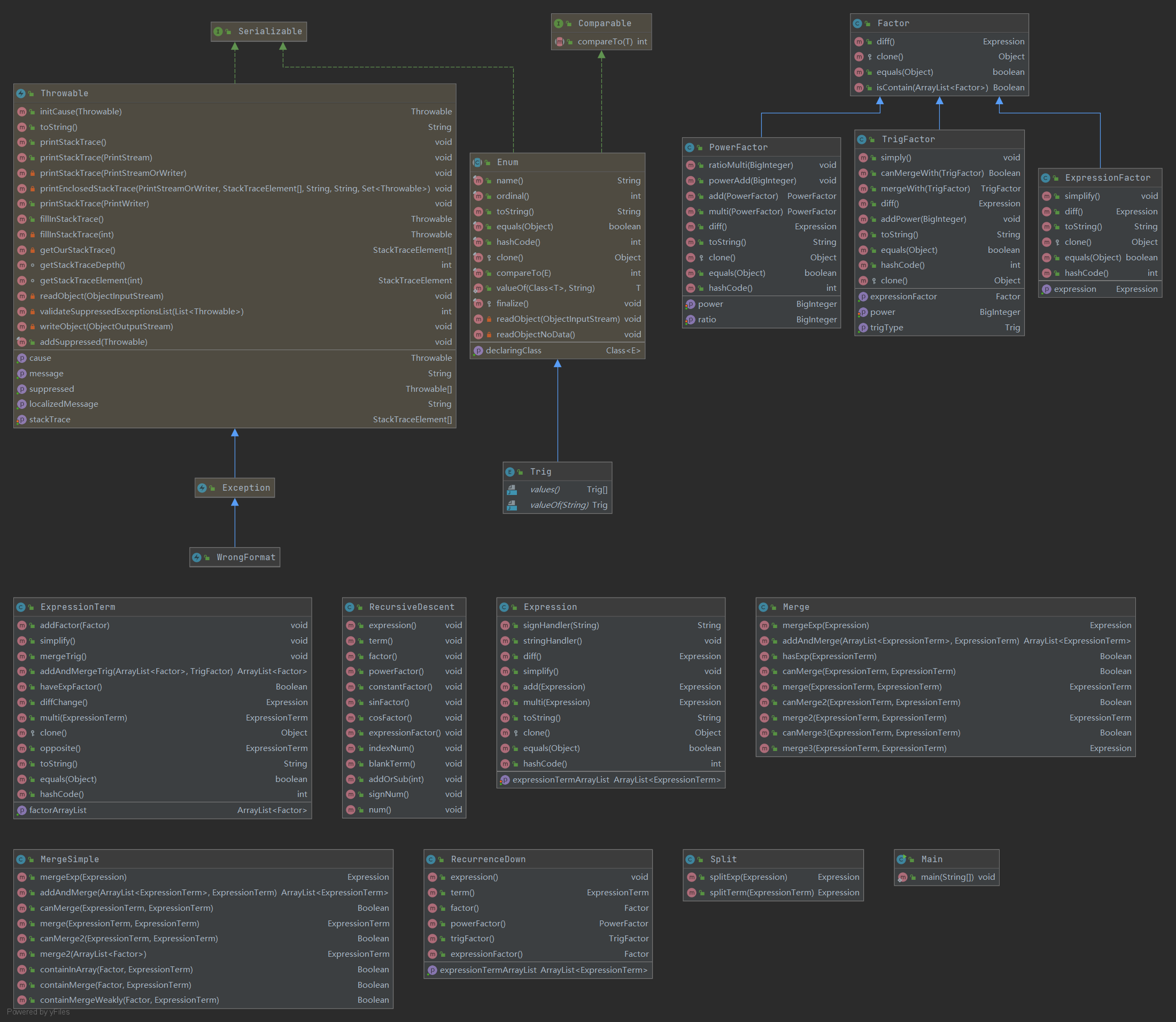
类的设计思路

• 整体思路和上次作业一样，但是为了判断是否格式错误写了一个新的类（一方面是因为原先解析表达式的类扛过了第二次的强测和互测我觉得正确性可以信赖，另一方面因为判断格式我想要写成纯粹的递归下降，如果要在这里面解析表达式，思路会和之前有区别），因此采用了加一个RecursiveDescent类来判断格式是否正确的方式。

• 自己定义了一个WrongFormat异常

• 求导公式采用课程组给出的求导公式，表达式，表达式项，表达式因子都有对应的求导方法

• 表达式的分级以及继承关系和上次作业完全一样，只是三角函数这个因子做了一些改动，第二次作业中三角函数中我加入的是一个表达式，根据本次作业的文法要求，更改成立一个表达式因子。

• 为没有写equals(),clone()方法的类都写了相应的equals,clone()方法，便于进行比较和深拷贝

• 因为三角函数不一定只有sin(x)和cos(x)两种情况，因此合并类做出了一些改变，这次只考虑了两种合并的情况写了用于合并的类MergeSimple

  1.两个项除系数之外完全相同，则可以合并

  2.两个项，提取出公因式之后，剩余的部分分别是是sin(因子1)**2，cos(因子2)**2,且因子1，因子2相同，则可以化简为公因式。

优点和缺点

• 优点

  采用了纯粹的递归下降去判断表达式是否符合格式要求，保证了格式判断的正确性，没有改动表达式解析的类，因此并没有做很大的改动

• 缺点

  1.整体的耦合度高，代码的测试难度较大。

  2.在判断得到格式正确之后，仍然采用了对输入做正则替换的方法替换掉空格，\t，和连续的加减号，程序的兼容性差，稍微修改一点文法带来的代码修改工作量大。

（二）自己程序的bug

第一次作业的强测和互测都没有bug，第二次作业的互测被找到了一个bug，因为第二次作业是在第一次作业上的迭代开发，因此直接复制粘贴了第一次的代码，但是粘贴了比较旧的版本，没有大整数的情况，因此出现了bug

第三次作业强测点错了四个点，互测被找到了一个bug，这些bug在更改中可以被归为三个

1.sin中嵌套的是一个表达式因子，虽然整个表达式在输出的时候如果全是0，会有一个特判，会输出0不会输出空，但是表达式因子不会有这个特判（为了让整体的表达式长度尽量短），最后分析的时候发现，一个表达式因子嵌套在sin中和单纯的出现在表达式的项中是不一样的，因此修改bug的时候特判了sin中嵌套0的情况。

2.为了判断输入是否符合格式要求，写了一个新的RecursiveDescent类，文法中有一条幂次数不能大于50，我觉得幂次不会很大，因此在递归下降记录幂次的时候把String转换成了Long从而对很大幂次的格式错误输入，会抛出异常。

3.本次作业在考虑拆括号的时候错误的认为拆括号会增加时间而且表达式会变长而没有拆括号，导致多层嵌套的表达式求导会超时，更改时把拆括号的操作又加了回来(因为保留了那个类，因此只是加了一个启动代码，没有引起很大篇幅的代码改动)。

（三）发现别人bug采用的策略

我发现别人bug主要是采用测评机去测试，数据是按照文法随机生成的数据，整个测评机用python编写，并没有构建一个普适性很强的测评机，数据也只是根据文法随机生成的，因此测试强度可能并不高，也有尝试过去读别人的代码来发现bug，但自己阅读代码的能力可能需要提升，因此主要的寻找bug的方式还是使用测评机自动测试。

（四）重构经历总结

在迭代开发期间有过大大小小不少次重构，其中比较大的两次都在第二次作业期间，第一次加入了三角函数因子和表达式因子，那个版本仍然在表达式类中解析表达式，第二次较大的重构把解析的工作交给了一个新写的递归下降类，第三次作业对于之前的代码几乎没有更改，只是增加了一个判断格式是否正确的类。

整体来看，重构的原因主要是为了满足新的函数和新的文法(允许表达式因子的存在)，重构中也在改善着自己的架构，尽量让程序变得可扩展性更好。

（五）心得体会

这是面向对象的第一单元，让我从之前的面向过程思想转换到了面向对象的思想，几次重构让我感受到了架构对一个程序来说的重要性，架构决定了一个程序的可扩展性，可读性和调试难度，第三次作业在提交之前用测评机测了很多组根据文法随机生成的数据并没有出现bug，但其实是有bug的，这让我认识到测评机的局限性和形式验证的必要性，在之后的作业中会注意这一点。