算法学习——递归之汉诺塔
算法描述
汉诺塔问题
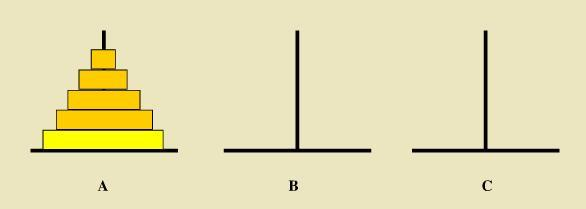
如下图所示,从左到右有A、B、C三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有一个原则:一次只能移到一个盘子且大盘子不能在小盘子上面,求移动的步骤和移动的次数
算法思路
-
1个盘的时候,只需要移动1次即可达成目标,
g(1) = 1)(步骤一) -
2个盘的时候,需要移动3次即可达成目标,
g(2) = 3(步骤二) -
3个盘的时候,我们需要将底下较大的两个盘先移动到C中,之后再将A中剩下的那个盘移动到C中。
这里需要注意的是,我们是将底下的2个盘当做了一个,所以是相当于进行了2次步骤二
需要2*g(2)次之后就是步骤一的那种情况 ,
需要1次移动g(3)=2*g(2)+1通式为
g(n)=2*g(n-1)+1递归出口为
n=1
算法实现
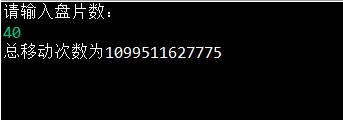
System.out.println("请输入盘片数:");
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
scanner.close();
long result = han(n);
System.out.println("总移动次数为"+result);
}
public static long han(int n){
long s;
if(n==1){
s=1;
}else{
s =2*han(n-1)+1;
}
return s;
}
结果