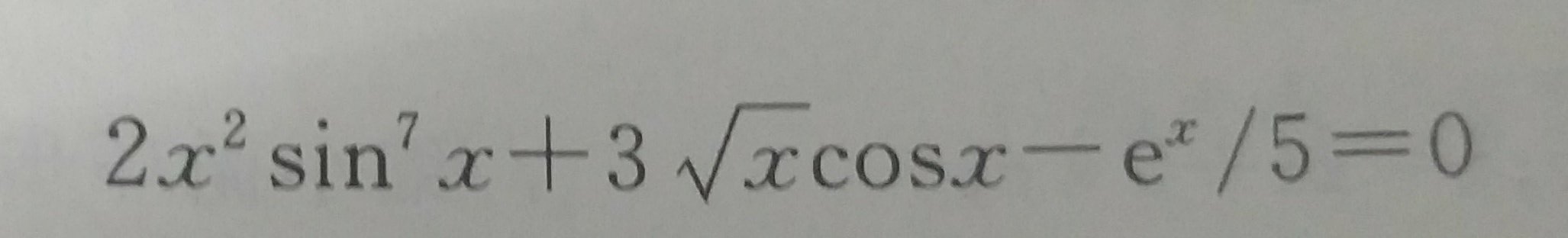算法学习——枚举之超级方程
算法描述
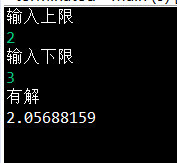
求区间(2,3)的一个解,精确到小数点后8位
算法思路
-
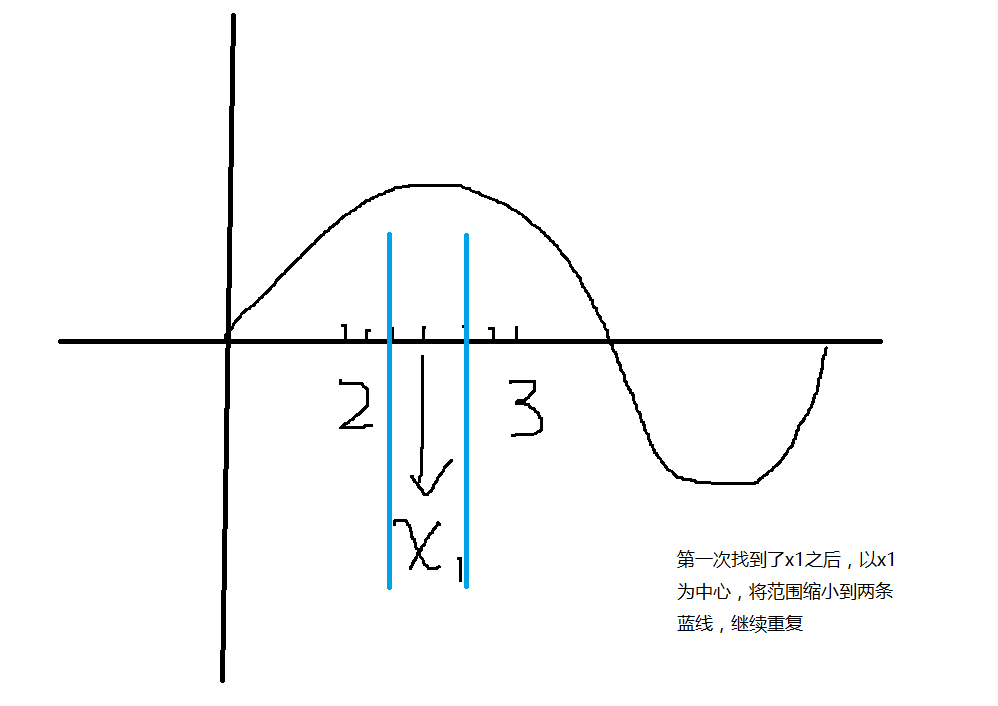
首先是要判断该区间是否有解,这里使用数学中的定义,
f(a)\*f(b)<0,则在a与b之间有解,我们从2开始,逐渐加0.1,与f(3)相乘,判断两者之积是否为0,即可知道是否有解 -
有解的话我们就可以继续下一步了,先设置一个数值min,从f(2)开始,一次加上0.1,寻找f(x)最小数值时候的x的值,以此x的值缩小范围,继续重复之前的步骤,经过多次循环之后,即可找到精度较大的x
算法实现
double a,b;
System.out.println("输入上限");
Scanner scanner = new Scanner(System.in);
a = scanner.nextInt();
System.out.println("输入下限");
b = scanner.nextInt();
scanner.close();
boolean isHave = false;//false无解
for(double i = a;i<=b;i=i+0.1){
if(fun(i)*fun(b)<=0){
isHave = true;
break;
}
}
if(isHave){
System.out.println("有解");
int k = 1;
double y,c = 0.1,min=100,x1=0;//min赋值一个较大的初值
while(k<=8){
for(double x=a;x<=b;x=x+c){
//System.out.println(x);
y = fun(x);
if(Math.abs(y)<min){
min = Math.abs(y);
x1 = x;
}
}
c = c/10;
//System.out.println(c);
a = x1-5*c;
b = x1+5*c;
k++;
}
DecimalFormat fm = new DecimalFormat("0.00000000");
System.out.println(fm.format(x1));
}else{
System.out.println("无解");
}
public static double fun(double x){
return 2*Math.pow(x, 2)*Math.pow(Math.sin(x), 7)+3*Math.pow(x, 0.5)*Math.cos(x)-Math.exp(x)/5;
}
结果