2020牛客暑期多校训练营第六场题解
2020牛客暑期多校训练营（第六场）
A. African Sort
假题。对于一个大小为 \(4\) 的环，我们第一次选前三个数字操作会得到比标解 \(\frac{34}{3}\) 更小的期望。
例如：我们要将
2 3 4 1变回1 2 3 4，第一次只变换前三个数字（即 \(2,3,4\)）。暴力枚举所有情况，显然有：2 3 4 1 2 4 3 1 3 2 4 1 3 4 2 1 4 2 3 1 4 3 2 1其中，
2 3 4 1和3 4 2 1都未变化，仍是大小为 \(4\) 的环；2 4 3 1和3 2 4 1有一个数字回到了原位置，变成了大小为 \(3\) 的环（期望为 \(\frac{15}{2}\)）；4 2 3 1有两个数字回到了原位置，变成了大小为 \(2\) 的环（期望为 \(4\)）；4 3 2 1变成了两个大小为 \(2\) 的环。综上，列出期望计算式：\[\begin{aligned}x&=\frac{x}{6}\times 2+\frac{2}{6}\times\frac{15}{2}+\frac{1}{6}\times 4+\frac{1}{6}\times8+3 \\x&=\frac{45}{4}<\frac{34}{3}\end{aligned} \]
B. Binary Vector
找规律发现本题公式为：
\[\begin{aligned}f_n=\prod^n_{i=1}\frac{2^i-1}{2^i}\end{aligned}
\]
由于要求的范围是 \(2e7\) ，并且要求异或前缀和，因此 \(O(n)\) 预处理出每一项 \(f_i\) ，然后做一个异或前缀和。
#include <bits/stdc++.h>
#define ll long long
using namespace std;
const ll mod = 1e9 + 7;
const int top = 2e7;
int fac[top + 10], two[top + 10], inv[top + 10], ans[top + 10];
ll qpow(ll a, ll b) {
ll res = 1;
for (; b; b >>= 1) {
if (b & 1) res = res * a % mod;
a = a * a % mod;
}
return res;
}
void init() {
fac[1] = 1;
ll base = 2ll;
two[1] = 2;
for (int i = 2; i <= top; ++i) {
base = (base * 2ll) % mod;
fac[i] = 1ll * fac[i - 1] * (base - 1ll) % mod;
two[i] = base;
}
inv[top] = qpow(qpow(2ll, 1ll * top * (top + 1ll) / 2ll), mod - 2ll);
for (int i = top - 1; i; --i)
inv[i] = 1ll * inv[i + 1] * two[i + 1] % mod;
ans[0] = 0;
for (int i = 1; i <= top; ++i) {
ll tmp = 1ll * inv[i] * fac[i] % mod;
ans[i] = (ans[i - 1] ^ tmp);
}
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
init();
int T; cin >> T;
while (T--) {
ll n; cin >> n;
cout << ans[n] << '\n';
}
return 0;
}
C. Combination of Physics and Maths
题意：选择矩阵的子矩阵，使得子矩阵和除子矩阵最底层的和值最大。
只要枚举每位当作底部元素，上方所有元素当作子矩阵即可，复杂度\(O(n*m)\)。
#include<bits/stdc++.h>
#define ll long long
#define maxn 100010
using namespace std;
ll a[210][210];
int main() {
int t;
scanf("%d", &t);
while (t--) {
int n, m;
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= m; j++) scanf("%lld", &a[i][j]);
}
double ans = 0;
for (int i = 1; i <= m; i++) {
ll sum = 0;
for (int j = 1; j <= n; j++) {
sum += a[j][i];
ans = max(ans, sum * 1.0 / a[j][i]);
}
}
printf("%.10lf\n", ans);
}
return 0;
}
E. Easy Construction
首先发现：由于我们的构造需要对任意 \(i\in [1,n]\) 都存在一个连续子序列使得其字段和等于 \(k\bmod n\) ，因此这个 \(k\) 必须满足 \(\frac{n(n+1)}{2}\bmod{n} = k\) 。
然后我们分奇偶构造，偶数时构造形如：n, k, 1, n - 1, 2, n - 2, ... 的数列（实际上，当 \(n\) 为偶数时 \(k=\frac{n}{2}\)，因此该构造成立）；奇数时构造形如：n, 1, n - 1, 2, n - 2, ... 的数列（因为 \(n\) 为奇数时，\(\frac{n(n+1)}{2}\bmod{n} = 0\)） 。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr); cout.tie(nullptr);
long long n, k;
cin >> n >> k;
vector<ll> ans;
ll res = ((n + 1ll) * n / 2ll) % n;
if (res != k) cout << -1;
else if (!(n & 1)) {
ans.push_back(n);
ans.push_back(k);
for (int i = 1; i < n / 2; ++i) {
ans.push_back(i);
ans.push_back(n - i);
}
for (auto i : ans) cout << i << ' ';
}
else {
for (int i = 0; i < n; i++) {
if (i % 2 == 0) cout << n - i / 2 << ' ';
else cout << (i + 1) / 2 << ' ';
}
}
return 0;
}
G. Grid Coloring
先按照如图所示的方法给网格图上的边标号：
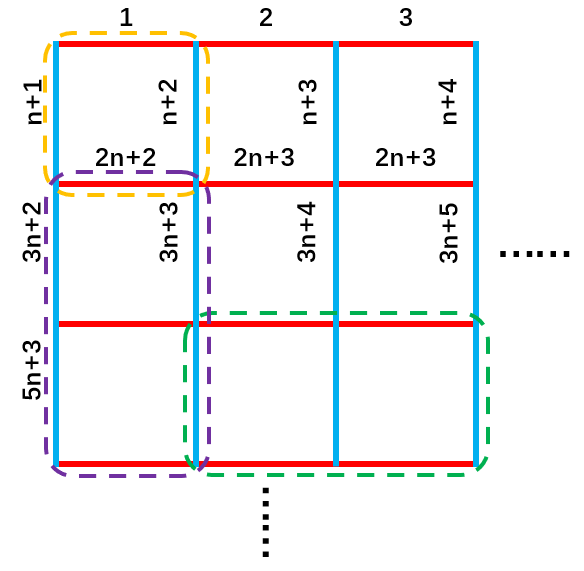
我们先考虑不可能构造的情况，再给出构造方案。不能构造的情况有：
- \(n=1\) 或 \(k=1\) ；
- \(2n(n+1)\bmod{k}\neq 0\) （其中 \(2n(n+1)\) 是图形的总边数）。
构造方案是：自顶向下分别给边按照 \(1\) 到 \(n\) 的顺序标号（如上图），然后我们将颜色 \(1\) 到 \(k\) 按照顺序轮流放到这些边上。（序号为 \(1\) 的边放颜色 \(1\) ，序号为 \(2\) 的边放颜色 \(2\) …… 序号为 \(k\) 的边放颜色 \(k\) ，序号为 \(k+1\) 的边放 \(1\) ，序号为 \(k+2\) 的边放 \(2\) ……）
然后，我们证明这样构造的正确性：
- 对于一个 \(1\times 1\) 的小环（如图中橙色框），它的两条纵边必定是相邻的序号，因此染的颜色必定不同；
- 对于任意一个 \(l\times (l+c),\ c>0\) 的环（如图中绿色框是一个 \(1\times 2\) 的环），它的横向边必定有相邻序号，因此染的颜色不同；同理可以证明所有横向边均不同色。
- 对于任意一个 \((l+c)\times l,\ c>0\) 的环（如图中紫色框是一个 \(2\times 1\) 的环），如果其横向边长 \(=1\) ，那么它就有相邻的纵向边；如果其横向边长 \(>1\) ，那么它就有相邻横向边。综上所述，任意一个环以及任意横边均不同色，因此我们只需要分析纵边是否同色。
我们最后证明，任意两条相邻纵向边必定不同色。观察上图，任意两条相邻纵向边的序号之差必定是 \(2n+1\) （图中所示的 \(n+1, 3n+2, 5n+3\) 均是相邻纵向边），于是我们只需要证明 \(\gcd(k,2n+1)=1\) ，即 \(2n+1\) 不能是一个循环节（\(k\)）的倍数。由于 \(k|2n(n+1)\) ，我们直接证明 \(\gcd(2n(n+1),2n+1)=1\) ：
\[\begin{aligned}&\gcd(2n(n+1),2n+1) \\\Leftrightarrow\ &\gcd(2n(n+1)-(2n+1)n,2n+1) \\\Leftrightarrow\ &\gcd(n, 2n+1 - n) \\\Leftrightarrow\ &\gcd(n, n+1) = 1\end{aligned}
\]
#include<bits/stdc++.h>
using namespace std;
int ans1[210][210], ans2[210][210];
int main() {
int t;
scanf("%d", &t);
while (t--) {
int n, k;
scanf("%d%d", &n, &k);
int sum = 2 * n * (n + 1);
if (n == 1 || sum % k || k == 1) {
printf("-1\n");
continue;
}
int now = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
now = now % k + 1;
ans1[i][j] = now;
}
for (int j = 0; j < n + 1; j++) {
now = now % k + 1;
ans2[j][i] = now;
}
}
for (int j = 0; j < n; j++) {
now = now % k + 1;
ans1[n][j] = now;
}
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < n; j++) printf("%d ", ans1[i][j]);
printf("\n");
}
for (int i = 0; i < n + 1; i++) {
for (int j = 0; j < n; j++) printf("%d ", ans2[i][j]);
printf("\n");
}
}
return 0;
}
H. Harmony Pairs
数位 \(DP\)
\(dp[pos][sub][euq]\) 前三位分别表示第 \(pos-1\) 位，前面\(pos-1\)位 数位和的差值，前面几位是否相等
数位 \(dp\) 每层暴力枚举 \(a\),\(b\) 下一位上的数字
- 若前面的几位相等,则该位上要求 \(a\leq b\)
- 否则 \(a,b\) 取任意值
然后记录 \(a、b\) 位数和之差
若递归到最后 \(sub>0\) 则可取，否则不可取
时间复杂度为 \(O(n^2*10^3)\)
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 105;
const LL mod = 1e9 + 7;
char s[maxn];
int len, a[maxn];
LL res[maxn][2005][2][2][2][2][2];
LL dfs2(int pos, int sub, bool euq, bool lead1, bool limit1, bool lead2, bool limit2) {
if (pos > len) {
if (euq) return 0;
return sub > 0;
}
if (res[pos][sub + 1000][euq][lead1][limit1][lead2][limit2] != -1)
return res[pos][sub + 1000][euq][lead1][limit1][lead2][limit2];
LL cnt = 0;
int top1 = limit1 ? a[pos] : 9;
int top2 = limit2 ? a[pos] : 9;
bool lead, limit;
for (int i = 0; i <= top1; i++) {
if ((!i) && lead1) lead = true;
else lead = false;
limit = (i == top1 && limit1);
if (!euq) {
for (int j = 0; j <= top2 && j < i; j++) {
if (!j && lead2)
cnt = cnt + dfs2(pos + 1, sub + i - j, euq && (i == j), lead, limit, true, j == top2 && limit2);
else
cnt = cnt + dfs2(pos + 1, sub + i - j, euq && (i == j), lead, limit, false, j == top2 && limit2);
cnt %= mod;
}
}
for (int j = i; j <= top2; j++) {
if (!j && lead2)
cnt = cnt + dfs2(pos + 1, sub + i - j, euq && (i == j), lead, limit, true, j == top2 && limit2);
else
cnt = cnt + dfs2(pos + 1, sub + i - j, euq && (i == j), lead, limit, false, j == top2 && limit2);
cnt %= mod;
}
}
res[pos][sub + 1000][euq][lead1][limit1][lead2][limit2] = cnt;
return cnt;
}
void doit() {
len = strlen(s + 1);
for (int i = 1; i <= len; i++)
a[i] = s[i] - '0';
memset(res, -1, sizeof(res));
cout << dfs2(1, 0, true, true, true, true, true) << '\n';
}
int main() {
scanf("%s", s + 1);
doit();
return 0;
}
J. Josephus Transform
因为约瑟夫环每次变换只与位置有关，可以看成
for (int i = 1; i <= n; i++)
a[p[i]] = a[i];
且 \(p\) 数组是全排列，那么就与上一次的全排列迭代相同。计算出每一位所在的环，可以很轻松得到每一位的循环节。
约瑟夫环的位置变换可以通过权值树状数组或者线段树得到：
删除第 \(x\) 个数后，下 \(k\) 个数通过二分得到（可以直接套二分，也可以树上二分）。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 5;
int a[maxn], h[maxn], p[maxn], v[maxn];
bool vis[maxn];
int cnt, g = 0;
vector<int> E[maxn];
void dfs(int now) {
vis[now] = true;
h[now] = g;
p[now] = cnt++;
E[g].push_back(a[now]);
if (!vis[v[now]]) dfs(v[now]);
}
int res[maxn];
int tree[maxn], limit;
inline int lowbit(int x) {
return x & -x;
}
void update(int x, int v) {
for (int i = x; i <= limit; i += lowbit(i))
tree[i] += v;
}
int query(int x) {
int res = 0;
for (int i = x; i; i -= lowbit(i))
res += tree[i];
return res;
}
void empty(vector<int>& a) {
vector<int> b;
swap(a, b);
}
int main() {
int n, q;
scanf("%d%d", &n, &q);
limit = n;
for (int i = 1; i <= n; i++) a[i] = i;
while (q--) {
int k, x;
scanf("%d%d", &k, &x);
for (int i = 1; i <= n; i++) update(i, 1);
int now = 0;
for (int i = 1; i <= n; i++) {
int least = query(n) - query(now);
int m = k;
int left, right, mid, ans;
if (least >= k) left = now + 1, right = n;
else {
now = 0;
m -= least;
m %= (n - i + 1);
if (!m) m = n - i + 1;
left = now + 1, right = n;
}
while (left <= right) {
mid = (left + right) >> 1;
if (query(mid) - query(now) >= m) {
right = mid - 1;
ans = mid;
}
else left = mid + 1;
}
now = ans;
v[i] = now;
update(now, -1);
}
g = 0;
fill(vis, vis + 1 + n, false);
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
cnt = 0;
g++;
dfs(i);
}
}
for (int i = 1; i <= n; i++)
a[i] = E[h[i]][(p[i] + x) % E[h[i]].size()];
for (int i = 1; i <= g; i++) empty(E[i]);
}
for (int i = 1; i <= n; i++) printf("%d ", a[i]);
printf("\n");
return 0;
}
K. K-Bag
首先正向遍历每个数，判断该数之前能否组成一个带前缀的K-Bag数组，然后添加断点。如果该数前k的位置为断点，且前k个数正好组成一个排列，便可添加断点。
然后反向处理带后缀的断点。如果正向断点和反向断点重合，便证明答案正确。
#include<bits/stdc++.h>
#define ll long long
#define maxn 500010
using namespace std;
int a[maxn], p1[maxn], p2[maxn];
int main() {
int t;
scanf("%d", &t);
while (t--) {
int n, k;
scanf("%d%d", &n, &k);
for (int i = 0; i <= n; i++) p1[i] = p2[i] = 0;
for (int i = 0; i < n; i++) scanf("%d", &a[i]);
unordered_map<int, int>m1, m2;
int sum = 0;
for (int i = 0; i < n; i++) {
int x = m1[a[i]];
if (i < k) {
m1[a[i]]++;
if (x == 0) sum++;
else if (x == 1) sum--;
if (sum == i + 1) p1[i] = 1;
}
else {
m1[a[i]]++;
if (x == 0) sum++;
else if (x == 1) sum--;
int y = m1[a[i - k]];
m1[a[i - k]]--;
if (y == 1) sum--;
else if (y == 2) sum++;
if (sum == k && p1[i - k]) p1[i] = 1;
}
}
int fl = 0;
sum = 0;
for (int i = 0; i < n; i++) {
if (i < k) {
int x = m2[a[n - 1 - i]];
m2[a[n - 1 - i]]++;
if (x == 0) sum++;
else if (x == 1) sum--;
if (sum == i + 1) p2[i] = 1;
}
else {
int x = m2[a[n - 1 - i]];
m2[a[n - 1 - i]]++;
if (x == 0) sum++;
else if (x == 1) sum--;
int y = m2[a[n - 1 - i + k]];
m2[a[n - 1 - i + k]]--;
if (y == 1) sum--;
else if (y == 2) sum++;
if (sum == k && p2[i - k]) p2[i] = 1;
}
if (p2[i] && p1[n - 2 - i]) {
fl = 1;
break;
}
}
if (p1[n - 1] || p2[n - 1]) fl = 1;
if (fl) printf("YES\n");
else printf("NO\n");
}
return 0;
}
