代码随想录Day23

题目列表

• 39.组合总和(LeetCode)
• 40.组合总和II(LeetCode)
• 131.分割回文串（LeetCode)

解题过程

39.组合总和

题目描述

解题思路

回溯中的组合问题，但是该问题中允许组合里的元素重复使用，所以在回溯三部曲中，startIndex 不需要在递归中排除当前已使用的元素，也就是在循环中调用递归函数时传参是 i.
剪枝操作：排序之后，如果 sum + 当前 已经大于 target,那么证明已经不符合条件。（本题代码中没有使用）。

代码展示

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        backtracking(candidates, target, 0, 0);
        return result;
    }
    public void backtracking(int[] candidates, int target, int sum,int start){
        if(sum > target) return;
        if(sum == target){
            result.add(new ArrayList<>(path));
            return;
        }
        for(int i = start; i < candidates.length; i++){
            path.add(candidates[i]);
            sum += candidates[i];
            backtracking(candidates, target, sum, i);
            path.removeLast();
            sum -= candidates[i];
        }
    }
}

40.组合总和II

题目描述

解题思路

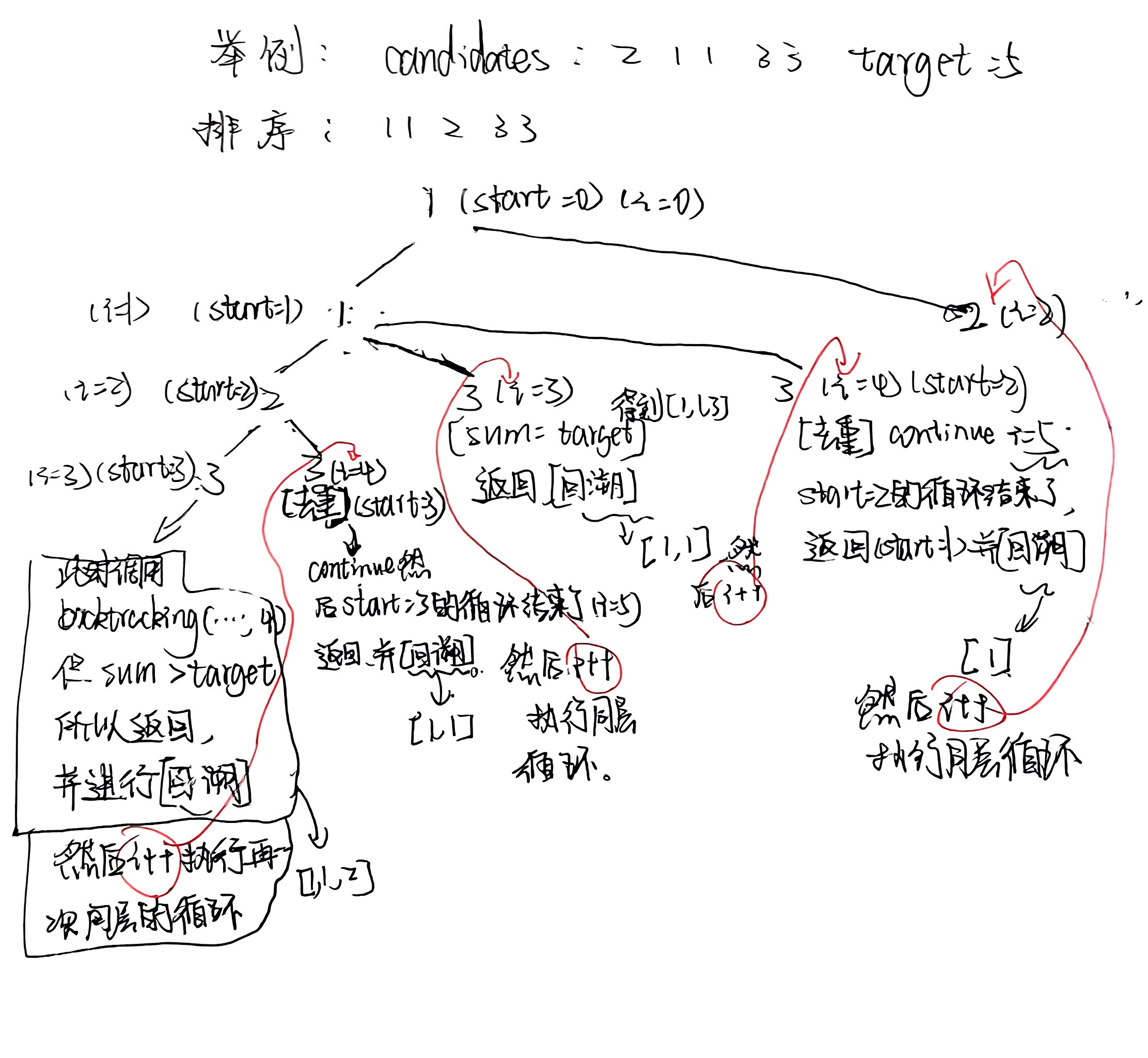
去重

根据题目给的示例可以看出，同一条“路径”上仅仅不允许使用已经使用过的元素（不能重复使用数组中下标相同的元素，下标不同数值相同是允许使用的）
而不同“路径”（也就是另一个结果集）中，不允许使用之前“路径”使用过的数值。因为如果允许的话，会出现两个或两个以上一样的组合，这是不正确的。
对于一条路径中的去重：
一条路径在代码中体现为“每一次元素的使用”都是在不同的循环体中（start不同的for循环），只需要保证下标相同的元素不重复使用，所以让 start == i + 1即可。
不同路径的去重：
不同路径在代码中体现为：在同一层for循环（start相同，也就是同一层递归中），要判断当前元素与前一个元素数值是否相同（i > start 且 candidates[i] == candidates[i - 1]）,相同就跳过，继续 i++.

代码展示

class Solution {
    List<List<Integer>> result = new ArrayList<>();
    List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        Arrays.sort(candidates);
        backtracking(candidates, target, 0, 0);
        return result;
    }
    public void backtracking(int[] candidates, int target, int sum, int start){
        if(sum == target){
            result.add(new ArrayList<>(path));
            return;
        }
        for(int i = start; i < candidates.length && sum + candidates[i] <= target; i++) {
            if(i > start && candidates[i] == candidates[i - 1]){
                continue;
            }
            path.add(candidates[i]);
            sum += candidates[i];
            backtracking(candidates, target, sum, i + 1);
            path.removeLast();
            sum -= candidates[i];
        }
    }
}

131.分割回文串

题目描述

解题思路

代码展示

class Solution {
    List<List<String>> result = new ArrayList<>();
    List<String> path = new ArrayList<>();
    public List<List<String>> partition(String s) {
        backtracking(s, new StringBuilder(), 0);
        return result;
    }
    public void backtracking(String s, StringBuilder sb, int start) {
        if(start == s.length()){
            result.add(new ArrayList<>(path));
            return;
        }

        for(int i = start; i < s.length(); i++){
            sb.append(s.charAt(i));
            if(isPalindrome(sb)){
                path.add(sb.toString());
            }else{
                continue; //同层递归中寻找下一个组合（重新切割）
            }
            //只有当前sb是回文子串才会继续这条路径
            backtracking(s, new StringBuilder(), i + 1);
            path.remove(path.size() - 1);

        }
    }
    public boolean isPalindrome(StringBuilder sb){
        for(int i = 0; i < sb.length()/2; i++){
            if(sb.charAt(i) != sb.charAt(sb.length() - 1 - i)){
                return false;
            }
        }
        return true;
    }
}

参考资料

代码随想录