代码随想录Day20

题目列表

• 669.修剪二叉搜索树(LeetCode)
• 108.将有序数组转换为二叉搜索树(LeetCode)
• 538.把二叉搜索树转换为累加树(LeetCode)

解题过程

669.修剪二叉搜索树

题目描述

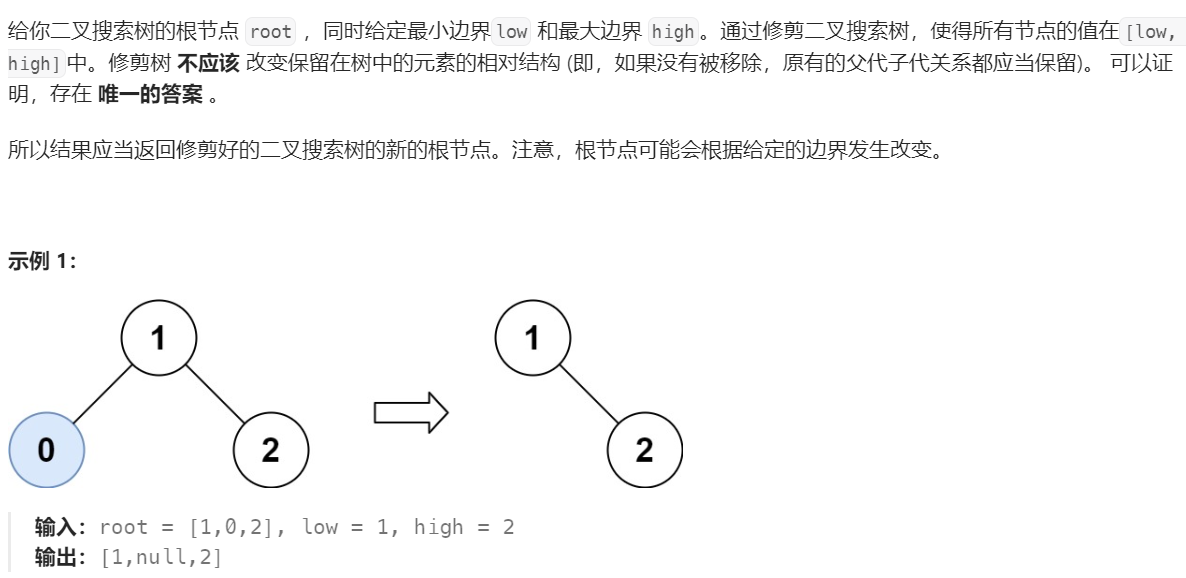
解题思路

修剪二叉搜索树，可以看作比较复杂的删除二叉搜索树的节点，那么为了保证二叉搜索树的结构，处理顺序还是要用后序遍历。

剪枝操作（提前删除不符合范围的节点）：
删除节点值在给定范围以外的节点，可以利用到二叉搜索树的特性。
也就是说，假如当前节点值小于最小边界，那么它的左子树一定也不符合条件，所以只用进一步考虑右子树就可以了（这里直接把右子树递归结果返回到当前节点，就代表删除root操作）。
同样的，假如当前节点值大于最大边界，那么它的右子树一定也不符合条件，所以只用进一步考虑左子树就可以了（这里直接把左子树递归结果返回到当前节点，就代表删除root操作）。

然后就是真正的后序遍历（只需要处理合法root）：
先递归处理左子树：root.left = 递归函数
再递归处理右子树：root.right = 递归函数
最后返回挂好所有符合条件子树的 root,这里直接返回 root,得益于前面的剪枝操作，得益于二叉搜索树的特性。

代码展示

class Solution {
    public TreeNode trimBST(TreeNode root, int low, int high) {
        if(root == null) return null;

        if(root.val < low) return trimBST(root.right, low, high);
        if(root.val > high) return trimBST(root.left, low, high);

        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;

    }
}

108.将有序数组转换为二叉搜索树

题目描述

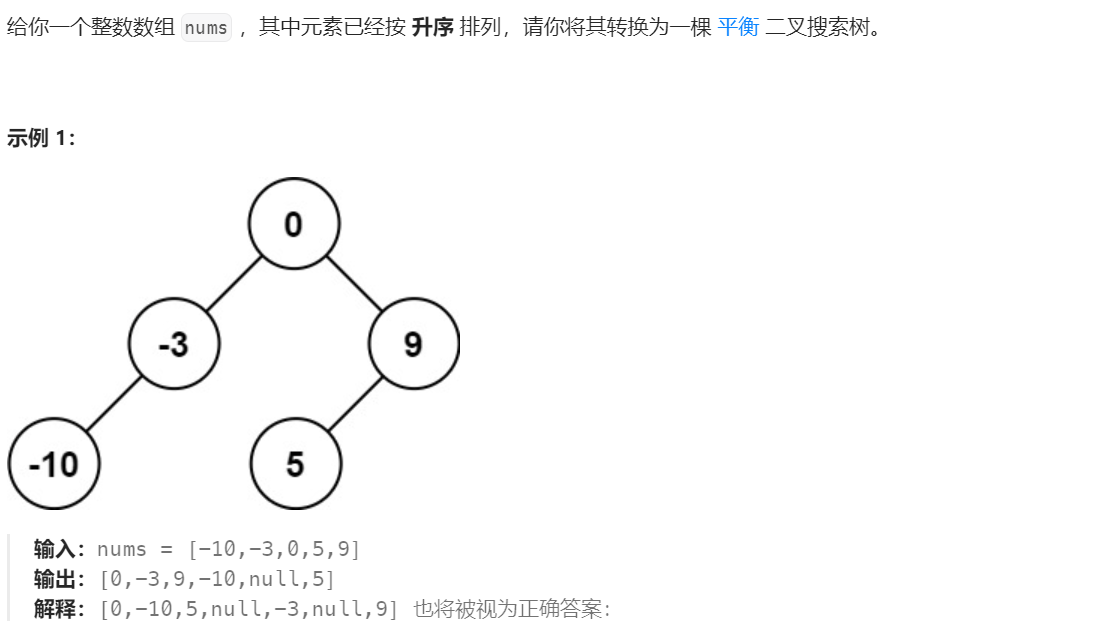
解题思路

要求是要平衡的二叉搜索树，那么从数组头开始构造就会很麻烦。利用数组有序且是二叉搜索树的特性，可以通过不断从中间分割，然后前序构建的方式进行递归。
我定义的是左闭右闭的区间进行分割。

代码展示

class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        if (nums.length == 0) return null;

        return arraytoBST(nums, 0, nums.length - 1);
    }
    public TreeNode arraytoBST(int nums[], int start, int end){
        if(start > end) return null;
        if(start == end) return new TreeNode(nums[start]);

        int mid = start + (end - start)/2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = arraytoBST(nums, start, mid - 1);
        root.right = arraytoBST(nums, mid + 1, end);
        return root; 
    }
 }

538.把二叉搜索树转换为累加树

题目描述

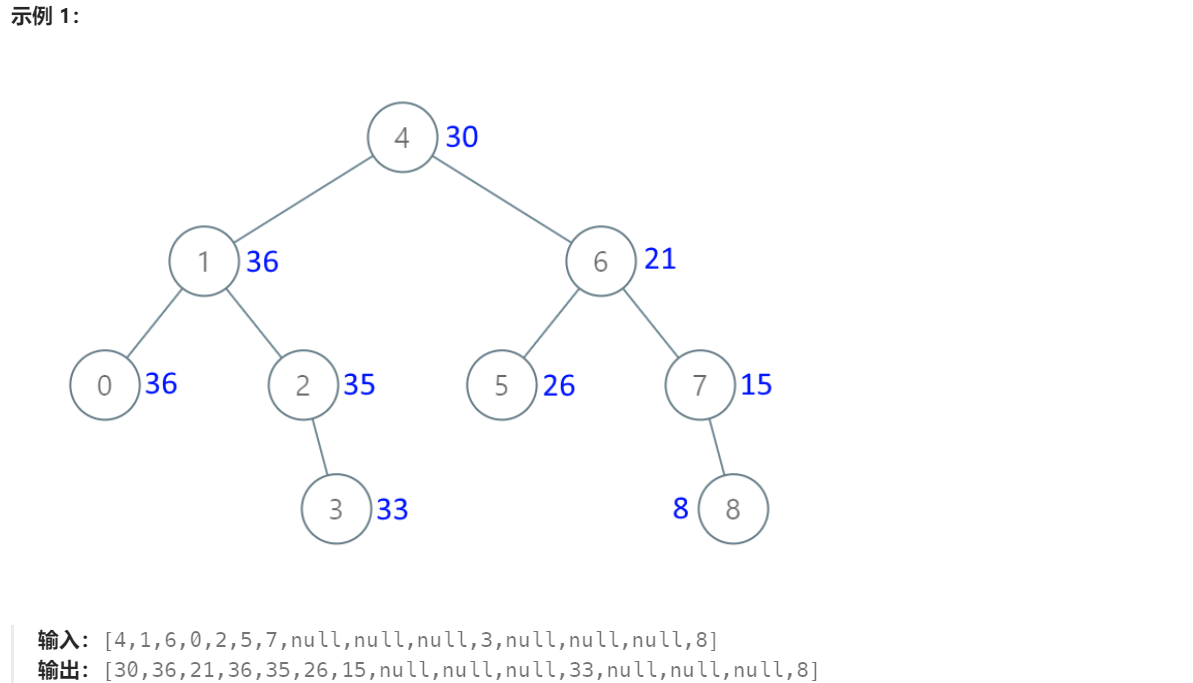
解题思路

一开始没看明白怎么累加的。
累加指的是，从树的最右边开始，根据 右-中-左 的方式不断累加，当前节点值 = 前一个节点值 + 当前节点值。所以需要一个指针记录上一个节点。
因为这道题目无需改变树的结构，但是要遍历整棵树，所以递归函数没有返回值。
根据右中左的顺序遍历并且累加即可。
终止条件就是遇到空节点直接返回。

代码展示

class Solution {
    TreeNode pre = new TreeNode(0);
    
    public TreeNode convertBST(TreeNode root) {
        if(root == null) return null;
        traversel(root);
        return root;
    }
    public void traversel(TreeNode root){
        if(root == null) return;

        traversel(root.right);
        root.val += pre.val;
        pre = root;
        traversel(root.left);
    }
}

参考资料

代码随想录