代码随想录Day13

题目列表

• 递归法：144.二叉树的前序遍历|94.二叉树的中序遍历|145.二叉树的后序遍历(LeetCode)
• 迭代法：144.二叉树的前序遍历|94.二叉树的中序遍历|145.二叉树的后序遍历(LeetCode)
• 统一迭代：144.二叉树的前序遍历|94.二叉树的中序遍历|145.二叉树的后序遍历(LeetCode)
• 102.二叉树层序遍历(LeetCode)

解题过程

递归法：144.二叉树的前序遍历|94.二叉树的中序遍历|145.二叉树的后序遍历

题目描述

给你一棵二叉树的根节点 root ，返回其节点值的 前序遍历 。
给你一棵二叉树的根节点 root ，返回其节点值的 中序遍历 。
给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

解题思路

• 首先明确前中后序遍历二叉树是什么顺序：
  前序遍历：中左右
  中序遍历：左中右
  后序遍历：左右中
• 然后知道左子树右子树这种形式适合递归，使用递归要明确三个要点：
  递归函数的参数和返回值类型；
  递归结束条件：也就是边界条件；
  一次递归的逻辑。

代码展示

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
//前序递归遍历
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        preorder(root,list);
        return list;
    }
    public void preorder(TreeNode root, List<Integer> list){
        if(root == null){
            return;
        }
        list.add(root.val);
        preorder(root.left,list);
        preorder(root.right,list);
    }
}
//中序递归遍历
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        inorder(root,list);
        return list;
    }
    public void inorder(TreeNode root, List<Integer> list){
        if(root == null){
            return;
        }
        inorder(root.left,list);
        list.add(root.val);
        inorder(root.right,list);
    }
}
//后序递归遍历
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        postorder(root,list);
        return list;
    }
    public void postorder(TreeNode root, List<Integer> list){
        if(root == null){
            return;
        }
        postorder(root.left,list);
        postorder(root.right,list);
        list.add(root.val);
    }
}

迭代法：144.二叉树的前序遍历|94.二叉树的中序遍历|145.二叉树的后序遍历

题目描述

给你一棵二叉树的根节点 root ，返回其节点值的 前序遍历 。
给你一棵二叉树的根节点 root ，返回其节点值的 中序遍历 。
给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

解题思路

• 前序
  前序遍历是中左右的顺序，在不使用递归的情况下，可以借助栈来保存遍历过的节点，并且在恰当时间返回。
  首先将根节点放到栈中，然后在循环中先处理栈顶元素（每次循环中处理的子树的中间节点），然后让右节点入栈，再让左节点入栈，左节点此时是栈顶元素，也就是下一次循环要处理的子树的中间节点，左子树处理完之后再处理右子树，一直到遍历完最后一个右节点，此时栈为空，循环结束。
• 中序
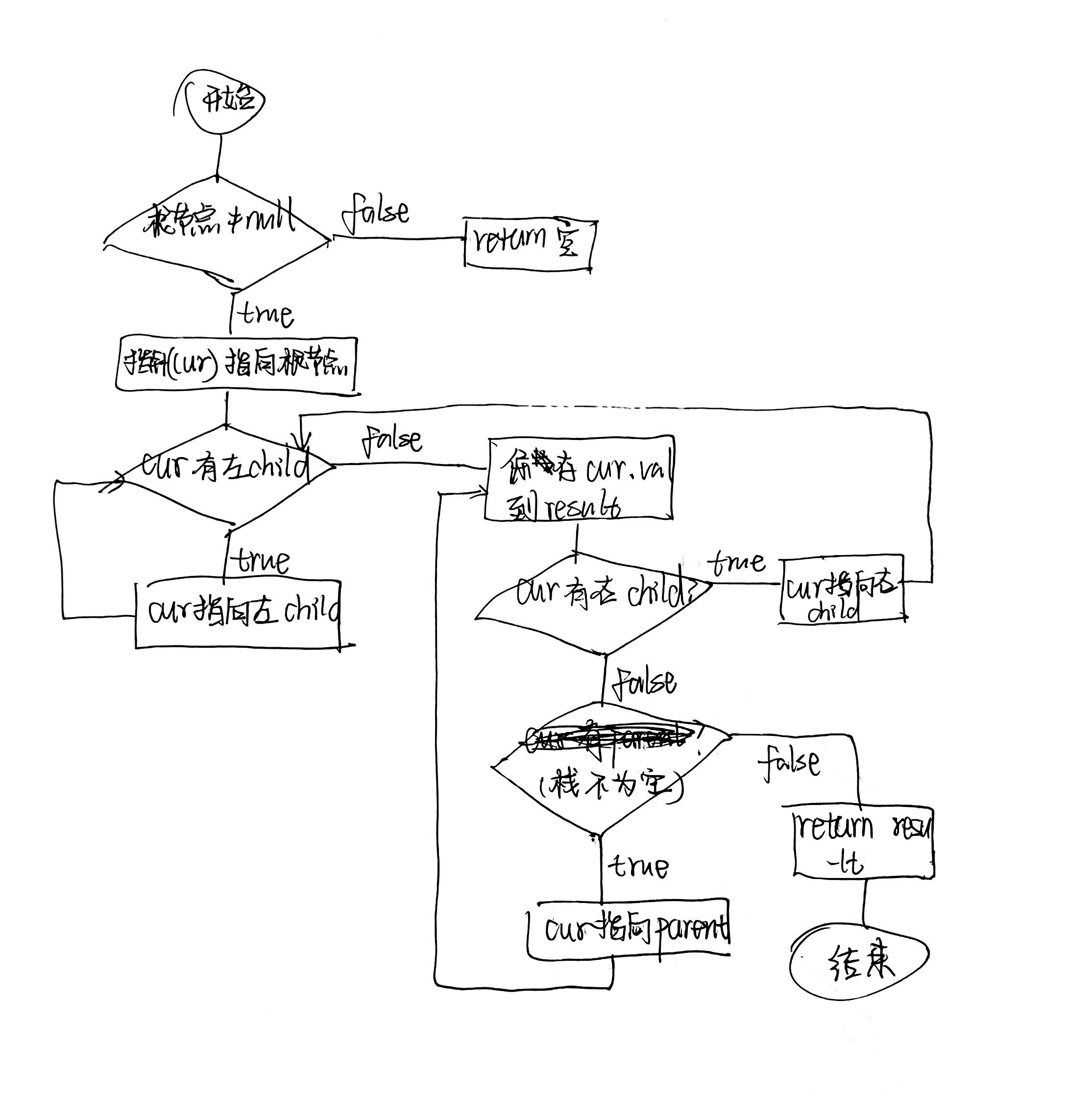
  中序遍历是左中右的顺序，可以想象我们是从根节点开始遍历这棵树的，但是在第一次遍历中间节点的时候我们不能对其做出处理，而是要继续寻找它的左 child 。
  流程图大致如下（代码中是先让 cur 指向左右 child 再判断 cur 是否为空的，流程图不大严谨）
  
• 后序
  后序是左右中的顺序，那么可以按照倒过来“中右左”的顺序进行遍历和保存，结束之后反转结果即可。

代码展示

//前序
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        //迭代
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack<>();

        if(root == null){
            return result;
        }

        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode cur = stack.pop();
            result.add(cur.val);
            if(cur.right != null){
                stack.push(cur.right);
            }
             if(cur.left != null){
                stack.push(cur.left);
            }
        }
        return result;

    }
}
//中序
//迭代
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        TreeNode cur = root;
        while (cur != null || !stack.isEmpty()){
           if (cur != null){
               stack.push(cur);
               cur = cur.left;
           }else{
               cur = stack.pop();
               result.add(cur.val);
               cur = cur.right;
           }
        }
        return result;
    }
    
    
}

//后序
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null){
            return result;
        }
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        while (!stack.isEmpty()){
            TreeNode node = stack.pop();
            result.add(node.val);
            //出栈顺序：右左
            if (node.left != null){
                stack.push(node.left);
            }
            if (node.right != null){
                stack.push(node.right);
            }
        }
        Collections.reverse(result);
        return result;
    }
}

统一迭代：144.二叉树的前序遍历|94.二叉树的中序遍历|145.二叉树的后序遍历(待做）

题目描述

给你一棵二叉树的根节点 root ，返回其节点值的 前序遍历 。
给你一棵二叉树的根节点 root ，返回其节点值的 中序遍历 。
给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

解题思路

代码展示

102.二叉树层序遍历

题目描述

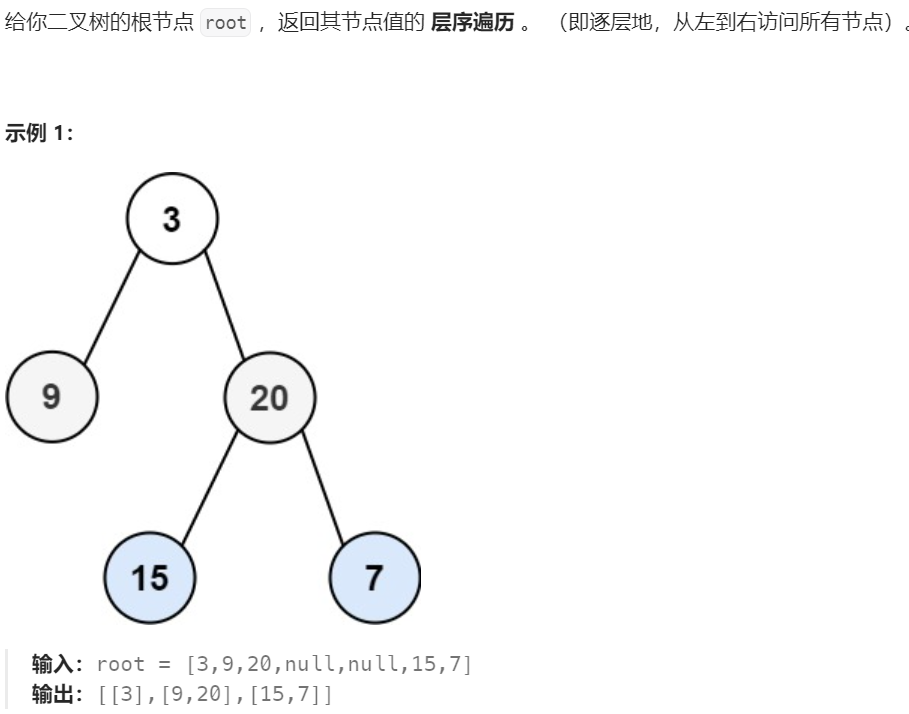
解题思路

使用一个队列，先将第一层放进去，记录第一层的大小 size ，每次遍历这一层的下一层，同时根据 size 将这一层放入结果中并弹出队列，此时队列大小作为下一次循环中弹出元素数目的依据。

代码展示

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        Queue<TreeNode> queue = new LinkedList<>();
        if(root == null) return result;
        queue.offer(root);

        while(!queue.isEmpty()){
            int size = queue.size();
            List<Integer> levelList = new ArrayList<>();
            while(size > 0){
                TreeNode cur = queue.poll();
                levelList.add(cur.val);
                if(cur.left != null) queue.add(cur.left);
                if(cur.right != null) queue.add(cur.right);
                size--;
            }
            result.add(levelList);
        }
        return result;
    }
}

参考资料

代码随想录