代码随想录Day12

题目列表

• 150.逆波兰表达式求值(LeetCode)
• 239.滑动窗口最大值(LeetCode)
• 347.前 K 个高频元素(LeetCode)

解题过程

150.逆波兰表达式求值

题目描述

解题思路

之前上编译原理课程时有接触过逆波兰式，逆波兰式就是后序遍历表达式对应的二叉树的结果，它的特点是操作符总是在两个操作数的后面，也就是说不管怎么样，一个操作符的前面的“两大块”就是这个操作符对应的操作数。
逆波兰式可以通过栈计算。从左到右扫描表达式，遇到操作数就压入栈中，遇到操作符就从栈中弹出相应数量的操作数进行计算，然后将结果压回栈中。最终栈顶的元素就是表达式的计算结果。

代码展示

class Solution {
    public int evalRPN(String[] tokens) {
        Stack<Integer> stack = new Stack<>();
        int result = 0;
        for(String s : tokens){
            if(isDigit(s)){
                stack.push(Integer.parseInt(s));
            }
            else{
                int a = stack.pop();
                int b = stack.pop();
                if(s.equals( "+")){
                   stack.push(a + b);
                }
                else if(s.equals("-")){
                    
                    stack.push(b - a);
                }
                else if(s.equals("*")){
                   
                    stack.push(b * a);
                }
                else if(s.equals("/")){
             
                    stack.push(b / a);
                }

            }
        }
        return stack.pop();
    }
    public boolean isDigit(String s){
         try {
            Integer.parseInt(s);
            return true;
        } catch (NumberFormatException e) {
            return false;
        }
    }
}

239.滑动窗口最大值

题目描述

解题思路

看了代码随想录的视频和题解，写了个数组模拟了下。

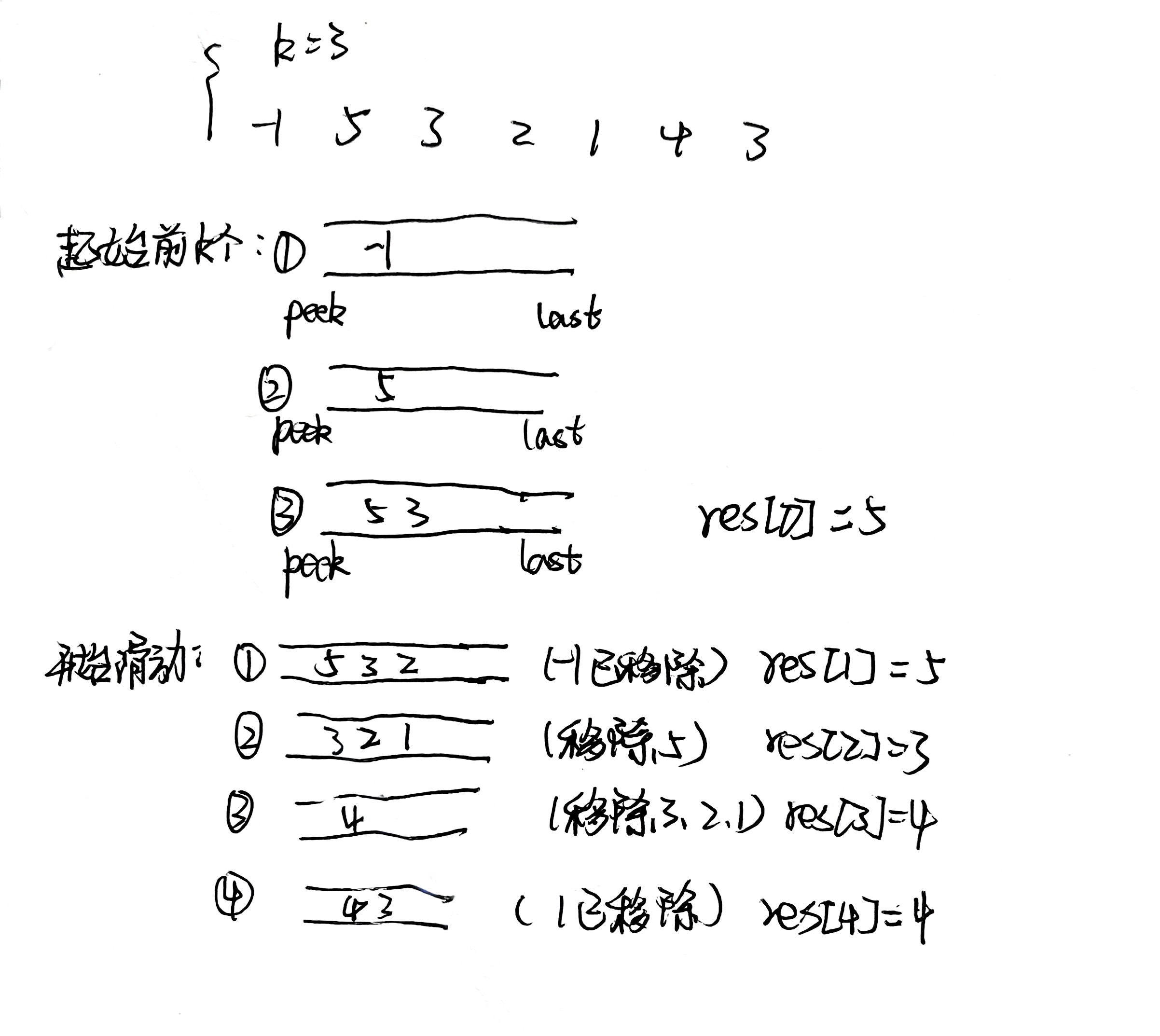
代码展示

class MyQueue{
    Deque<Integer> deque = new LinkedList<>();

    void poll(int val){
        if(!deque.isEmpty() && deque.peekFirst() == val){
            //队头出
            deque.pollFirst();
        }
    }

    void push(int val){
        while(!deque.isEmpty() && val > deque.getLast()){
            //删队尾
            deque.removeLast();
        }
        //队尾进
        deque.offerLast(val);
    }

    int peek(){
        return deque.peek();
    }

}
class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
         MyQueue myqueue = new MyQueue();
        int res[] = new int[nums.length - k + 1];
        //处理前k个元素
        for(int i = 0; i < k; i++){
            myqueue.push(nums[i]);
        }
        res[0] = myqueue.peek();

        //滑动窗口开始移动
        for(int i = k; i < nums.length; i++){
            myqueue.poll(nums[i - k]);
            myqueue.push(nums[i]);
            res[i - k + 1] = myqueue.peek();
        }
        return res;
    }
}

347.前 K 个高频元素

题目描述

解题思路

https://programmercarl.com/0347.前K个高频元素.html#算法公开课

注意事项

小顶堆

优先队列比较规则

代码展示

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        Map<Integer,Integer> map = new HashMap<>();
        for(int i : nums){
            map.put(i, map.getOrDefault(i, 0)+1);
        }
        /*
        *Lambda 表达式，用于定义 PriorityQueue（优先队列/堆）的 比较规则。
        pair1 和 pair2 是优先队列中的两个元素（这里是 int[2] 数组，存储 [数字, 出现次数]）。
        pair1[1] - pair2[1] 表示按 出现次数（pair[1]）从小到大排序（小顶堆）。
        如果 pair1[1] - pair2[1] < 0，说明 pair1 的出现次数更少，应该排在前面。
        如果 pair1[1] - pair2[1] > 0，说明 pair2 的出现次数更少，应该排在前面。
        如果 = 0，则两者相等，顺序无关紧要。
        */
        PriorityQueue<int[]> pq = new PriorityQueue<>((pair1, pair2) -> pair1[1] - pair2[1]);
        for(Map.Entry<Integer, Integer> entry : map.entrySet()){
           if (pq.size() < k) {
                pq.add(new int[]{entry.getKey(), entry.getValue()});
            } else {
                if (entry.getValue() > pq.peek()[1]) {
                    pq.poll(); 
                    pq.add(new int[]{entry.getKey(), entry.getValue()});
                }
            }
        }
        int res[] = new int[k];
        for(int i = k - 1; i >= 0;i--){
            res[i] = pq.poll()[0];
        }
        return res;
    }
}

参考资料

代码随想录