Matlab信号处理基础

一. 简介

　　离散傅立叶、离散余弦和离散小波变换是图像、音频信号常用基础操作，时域信号转换到不同变换域以后，会导致不同程度的能量集中，信息隐藏利用这个原理在变换域选择适当位置系数进行修改，嵌入信息，并确保图像、音频信号经处理后感官质量无明显变化。

二. 数学公式

一维离散傅立叶变换对定义

一维离散傅里叶变换：

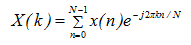
一维离散傅里叶逆变换：

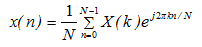
一维离散余弦变换对定义

一维离散余弦正变换：

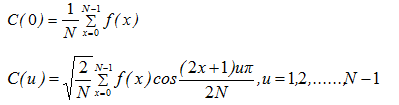
一维离散余弦反变换：

 

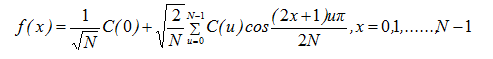
一维连续小波变换对定义

一维连续小波变换，其总h(t)是小波母函数：

 

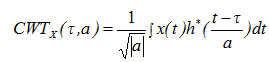
一维连续小波逆变换：

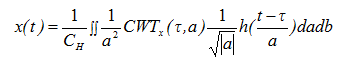
二维离散傅立叶变换对定义

二维离散傅里叶变换：

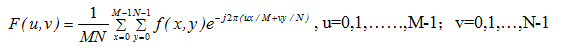
二维离散傅里叶逆变换：

二维离散余弦变换对定义

二维离散余弦正变换：

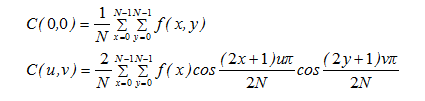
二维离散余弦反变换：

 

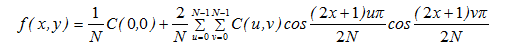
三. 代码实现

1. 用离散傅里叶变换分析合成音频和图像

（1）分析合成音频文件

第一步：读取音频文件数据。

 　　uigetfile() 是文件对话框函数，提供图形界面供用户选择所需文件，返回目标的目录名和文件名。

 　　函数原型：y= wavread (FILE)

     　　功能：读取微软音频格式（wav）文件内容

    　　输入参数：file 表示音频文件名，字符串

    　　返回参数：y 表示音频样点，浮点型

第二步：一维离散傅立叶变换

　　fft 函数对输入参数进行一维离散傅立叶变换并返回其系数，对应频率从 0 到 fs（采样频率），使用 fftshift 将零频对应系数移至中央。为了更好地观察频谱，可计算离散样点对应的频率值。

第三步：一维离散傅立叶逆变换

　　ifft 函数对输入参数进行一维离散傅立叶逆变换并返回其系数。

第四步：观察结果

　　figure(n)表示创建第 n 个图形窗。

　　subplot 是子绘图函数，第一、二个参数指明子图像布局方式，例如，若参数为 2，3 则表示画面共分为 2 行，每行有 3 个子图像。第三个参数表明子图像序号，排序顺序为从左至右，从上至下。

　　plot 是绘图函数，默认使用方式为 plot(y)，参数 y 是要绘制的数据；如果需要指明图像横轴显示序列，则命令行为 plot(x, y)，默认方式等同于 plot ([0..len-1], y)，len为序列y的长度。

例

 

len=40000;
[fn,pn]=uigetfile('*.wav','请选择音频文件');
[x,fs]=wavread(strcat(pn,fn),len); %strcat()连接生成文件绝对路径

%一维离散傅里叶变换
xf=fft(x); 
f1=[0:len-1]*fs/len;
xff=fftshift(xf);　　% fftshift()将零频对应系数移至中央
h1=floor(len/2);　　 %取不大于len/2的最大整数
f2=[-h1:h1]*fs/len; 

%一维离散傅里叶逆变换
xsync=ifft(xf); 
figure;
subplot(2,2,1);plot(x);title('原始图像');
subplot(2,2,2);plot(xsync);title('synthesiaze audio');
subplot(2,2,3);plot(f1,abs(xf));title('fft coef. of audio'); %abs()求整数的绝对值
subplot(2,2,4);plot(f2(1:len),abs(xff));title('fftshift coef. of audio');

 

 

 

　

（2）分析合成图像文件

第一步：读取图像文件数据

 　　函数原型：A = imread(filename,fmt)

 　　功能：读取 fmt 指定格式的图像文件内容

 　　输入参数：filename 表示图像文件名，字符串。Fmt 表示图像文件格式名，字符串，函数支持的图像格式包括：JPEG，TIFF，GIF，BMP 等等，当参数中不包括文件格式名时，函数尝试推断出文件格式。

 　　返回参数：A 表示图像数据内容，整型。

 　　rgb2gray 函数将 RGB 图像转换为灰度图。

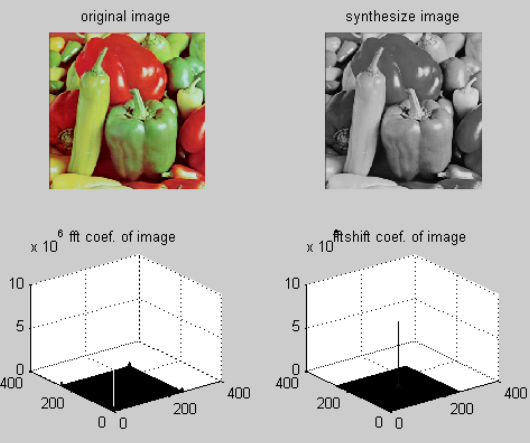
第二步：二维离散傅立叶变换

　　fft2 函数对输入参数进行二维离散傅立叶变换并返回其系数，使用 fftshift 将零频对应系数移至中央。

第三步：二维离散傅立叶逆变换

　　ifft2 函数对输入参数进行二维离散傅立叶逆变换并返回其系数。

第四步：观察结果

　　imshow 是二维数据绘图函数，mesh 通过三维平面显示数据。

例：

 

[fn,pn]=uigetfile('*.bmp','请选择图像文件');
[x,map]=imread(strcat(pn,fn),'bmp');
I=rgb2gray(x);　　%rgb2gray函数将 RGB 图像转换为灰度图

%二维离散傅立叶变换
xf=fft2(I);
xff=fftshift(xf);

%二维离散傅立叶逆变换
xsync=ifft2(xf);

%结果
figure;
subplot(2,2,1);imshow(x);title('original image');
subplot(2,2,2);imshow(uint8(abs(xsync)));title('synthesize image');
subplot(2,2,3);mesh(abs(xf));title('fft coef. of image');
subplot(2,2,4);mesh(abs(xff));title('fftshift coef. of image');

 

 

 

 

 

2. 用离散余弦变换分析合成音频和图像

（1）分析合成音频文件

第一步：读取音频文件数据。

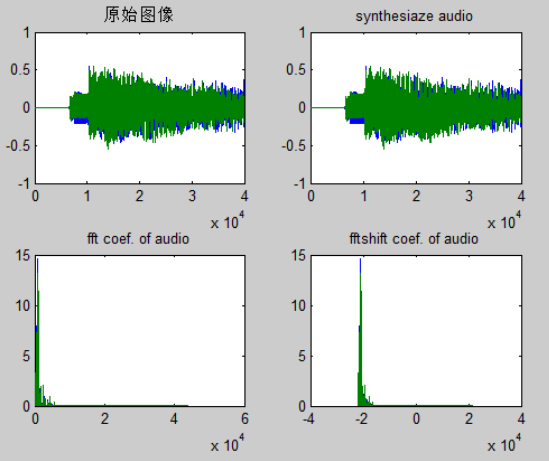
第二步：一维离散余弦变换

　　dct 函数对输入参数进行一维离散余弦变换并返回其系数，对应频率从0到 fs（采样频率）。

第三步：一维离散余弦逆变换

　　idct 函数对输入参数进行一维离散余弦逆变换并返回其系数。离散余弦变换常用于图像压缩，可以尝试只使用部分系数重构语言，通过观察可发现，原始音频和合成后音频两者差别不大。

第四步：观察结果

例：

len=40000;
[fn,pn]=uigetfile('*.wav','请选择音频文件');
[x,fs]=wavread(strcat(pn,fn),len);

%一维离散余弦变换
xf=dct(x);
f1=[0:len-1]*fs/len;
h1=floor(len/2);
f2=[-h1:h1]*fs/len; 

%一维离散余弦逆变换
xsync=idct(xf);
[row,col]=size(x);
xff=zeros(row,col);
xff(1:row,1:col)=xf(1:row,1:col);
y=idct(xff);

%结果
figure;
subplot(2,2,1);plot(x);title('原始图像');
subplot(2,2,2);plot(xsync);title('synthesiaze audio');
subplot(2,2,3);plot(f1,abs(xf));title('fft coef. of audio');
subplot(2,2,4);plot(f2(1:len),abs(xff));title('fftshift coef. of audio');

 

 

（2）分析合成图像文件

第一步：读取图像文件数据

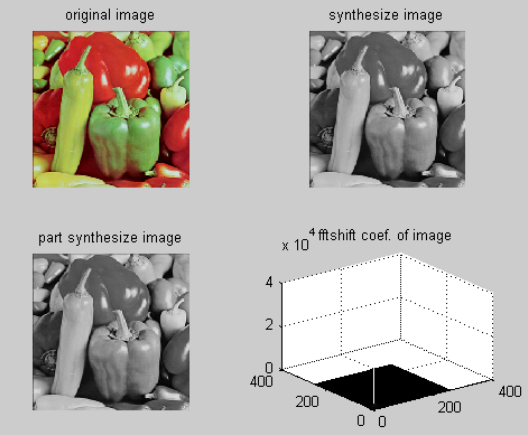
第二步：二维离散余弦变换

　　dct 函数对输入参数进行二维离散余弦变换并返回其系数。

第三步：二维离散余弦逆变换

　　idct2 函数对输入参数进行二维离散余弦逆变换并返回其系数。可以尝试使用部分系数重构图像，例如使用系数矩阵中4/5的数据，其它部分置零。

　　为了保证图像能正确显示，使用uint8 对重构图像原始数据进行了数据类型转换，确保其取值范围在 0 到 255 之间。

第四步：观察结果

    请输入命令显示四个子图，分别是原始图像、使用全部系数恢复的图像，使用部分系数恢复的图像和用三维立体图方式显示系数。

例：

[fn,pn]=uigetfile('*.bmp','请选择图像文件');
[x,map]=imread(strcat(pn,fn),'bmp');
I=rgb2gray(x);

%二维离散余弦变换
xf=dct2(I);

%二维离散余弦逆变换
xsync=uint8(idct2(xf));
[row,col]=size(I);
lenr=round(row*4/5);
lenc=round(col*4/5);
xff=zeros(row,col);
xff(1:lenr,1:lenc)=xf(1:lenr,1:lenc);
y=uint8(idct2(xff));

%结果
figure;
subplot(2,2,1);imshow(x);title('original image');
subplot(2,2,2);imshow(uint8(abs(xsync)));title('synthesize image');
subplot(2,2,3);imshow(uint8(abs(y)));title('part synthesize image');
subplot(2,2,4);mesh(abs(xff));title('fftshift coef. of image');

 

 

 

3. 用离散小波变换分析合成音频和图像

（1）分析合成音频文件

第一步：读取音频文件数据。

第二步：一维离散小波变换

　　wavedec 函数对输入参数进行一维离散小波变换并返回其系数C 和各级系数长度L。第二个参数指明小波变换的级数，第三个参数指明小波变换使用的小波基名称。

第三步：一维离散小波逆变换

　　waverec 函数对输入参数进行一维离散小波逆变换并返回其系数。

　　appcoef 函数返回小波系数近似分量，第一个参数 C、第二个参数 L 是 wavedec 的返回参数，为各级小波系数和其长度，第三个参数指明小波基名称，第四个参数指明级数。

　　detcoef 函数返回小波系数细节分量，第一个参数 C、第二个参数 L 是 wavedec 的返回参数，为各级小波系数和其长度，第三个参数指明级数。

第四步：观察结果

 例：

len=40000;
[fn,pn]=uigetfile('*.wav','请选择音频文件');
[x,fs]=wavread(strcat(pn,fn),len);

%一维离散小波变换
[C,L]=wavedec(x,2,'db4');

%一维离散小波逆变换
xsync=waverec(C,L,'db4');
cA2=appcoef(C,L,'db4',2);
cD2=detcoef(C,L,2);
cD1=detcoef(C,L,1);

%结果
figure;
subplot(2,3,1);plot(x);title('原始图像');
subplot(2,3,2);plot(xsync);title('synthesiaze audio');
subplot(2,3,4);plot(cA2);title('app coef. of audio');
subplot(2,3,5);plot(cD2);title('det coef. of audio');
subplot(2,3,6);plot(cD1);title('det coef. of audio');

 

 

（2）分析合成图像文件

第一步：读取图像文件数据

第二步：二维离散小波变换

　　dwt2函数对输入参数进行二维一级离散小波变换并返回近似分量，水平细节分量，垂直细节分量和对角线细节分量。如果要对图像进行多级小波分解，使用wavedec2函数。

第三步：二维离散小波逆变换

　　idwt2 函数对输入参数进行二维离散小波逆变换并返回其系数。可以尝试仅使用近似分量、水平细节分量、垂直细节分量或对角线细节分量重构图像。

第四步：观察结果

　　输入命令显示六个子图，分别是原始图像、使用全部系数恢复的图像、小波系数近似分量、水平细节分量、垂直细节分量和对角线细节分量。

例：

[fn,pn]=uigetfile('*.bmp','请选择bmp格式图像文件');
[x,map]=imread(strcat(pn,fn),'bmp');
I=rgb2gray(x);

%二维离散小波变换
sx=size(I);
[cA1,cH1,cV1,cD1]=dwt2(I,'bior3.7');

%二维离散小波逆变换
xsync=uint8(idwt2(cA1,cH1,cV1,cD1,'bior3.7',sx));
A1=uint8(idwt2(cA1,[],[],[],'bior3.7',sx));
H1=uint8(idwt2([],cH1,[],[],'bior3.7',sx));
V1=uint8(idwt2([],[],cV1,[],'bior3.7',sx));
D1=uint8(idwt2([],[],[],cD1,'bior3.7',sx));

%结果
figure;
subplot(2,3,1);imshow(x);title('original image');
subplot(2,3,2);imshow(uint8(abs(xsync)));title('synthesize image');
subplot(2,3,3);mesh(A1);title('app coef. of image');
subplot(2,3,4);mesh(H1);title('hor coef. of image');
subplot(2,3,5);mesh(V1);title('ver coef. of image');
subplot(2,3,6);mesh(D1);title('dia coef. of image');