ZR 集训前补题记录

Day 1（2025.6.27）

AT_abc221_h

简述题意：给定正整数 \(N,M\)，对于每个 \(1\le k \le N\)，求长度为 \(k\)，元素和为 \(N\)，每个数出现次数不超过 \(M\) 的正整数可重集个数，对 998244353 取模。

考虑去掉出现次数限制。

考虑钦定可重集的大小顺序，转化问题为统计不同的单调序列个数。

考虑一种非常妙的转化：钦定大小顺序为从大到小。每次我们都可以往序列末尾加一个 \(0\) 或者给整体加上 \(1\)。

这样定义 \(f_{i,j}\) 表示目前有 \(i\) 个数，和为 \(j\) 的方案数。有显然的转移：

• \(f_{i,j} \gets \sum\limits_{k=1}^i f_{i-k,j}\)
• \(f_{i,j} \gets f_{i,j - i}(j \ge i)\)

加入限制后发现只需要更改第一条式子就可以了，定义 \(g_{i,j}\) 为目前有 \(i\) 个数，和为 \(j\) 且没有数为 \(0\) 的方案数

• \(f_{i,j} \gets \sum\limits_{k=1}^m g_{i-k,j}\)
• \(f_{i,j} \gets f_{i,j - i}(j \ge i)\)
• \(g_{i,j} \gets f_{i,j - i}\)（整体加 \(1\) 即合法）

前缀和优化即可。

P9196

简述题意：给定 \(n\) 个字符串，\(m\) 个询问。每次询问给定字符串 \(P\) 和 \(Q\)，求出同时以 \(P\) 为前缀和 \(Q\) 为后缀的字符串个数。字符集大小为 \(4\)。

看到前缀、后缀字符串个数，考虑建出字典树。

前缀正插入，后缀倒插入。将 \(P\) 按正序跳到指定结点 \(p\) 和 \(Q\) 按倒序跳到 \(q\)。

显然，跳不到说明不存在，跳到后满足条件的串必然同时位于以 \(p\) 和 \(q\) 为根的子树内。

判断是否在子树内的问题用 dfn 转化为区间问题。

把字符串的结尾结点在正插入的树和倒插入的树中的 dfn 看作二维平面上的点，\(p\) 和 \(q\) 子树代表的区间看作矩形，问题转化为离线二维数点，直接做即可。

Day 2（2025.6.28）

P9108

简述题意：求长度为 \(n\) 的不同的区间序列个数，使得相邻的区间交集不为空且每个区间是 \([1,m]\) 的一个子区间。答案对 \(p\) 取模。

有一种比较显然的 DP。定义 \(dp_{i,l,r}\) 表示前 \(i\) 个区间，第 \(i\) 个区间是 \([l,r]\) 的方案数。转移是：\(dp_{i,l,r}=\sum\limits_{x=1}^r\sum\limits_{y=\max(x,l)}^m dp_{i-1,x,y}\)。

暴力转移超时。注意到式子不好刻画，考虑容斥，扣掉无交集的区间。

\[dp_{i,l,r}=\sum\limits_{x=1}^m\sum\limits_{y=x}^m dp_{i-1,x,y} - \sum\limits_{x=1}^{l-1}\sum\limits_{y=x}^{l-1} dp_{i-1,x,y} - \sum\limits_{x=r+1}^{m}\sum\limits_{y=x}^{m} dp_{i-1,x,y} \]

使用前缀和的思想优化状态。

定义：\(f_{i,j}=\sum\limits_{x=1}^j\sum\limits_{y=x}^j dp_{i,x,y}\)，\(g_{i,j}=\sum\limits_{x=j}^m\sum\limits_{y=x}^m dp_{i,x,y}\)。于是 \(dp_{i,l,r}=f_{i-1,m}-f_{i-1,l-1}-g_{i-1+r+1}\)。

带到原转移方程去，发现可以使用前缀和优化。且 \(f_{n,m}\) 恰好就是答案。

AT_abc412_e

简述题意：定义 \(f(x)=\text{lcm}(1,2,\ldots,x)\)，求 \(\{f(L),f(L+1),\ldots,f(R)\}\) 中不同数的个数。

分析不同的条件。

假设 \(f(y)=f(x)\) 且 \(y<x\)，那么必然存在 \(x \mid f(y)\)。同时又由于 \(f(y) \mid f(x-1)\)，所以 \(x \mid f(x-1)\)。这个条件是充要的。

如果不同，那么说明 \(x \nmid f(x-1)\)。即 \(x\) 中存在一个质因数指数比 \(1\sim x-1\) 中的最大指数还要大。

设 \(x=p^k\times c(c>1)\)。但由于 \(y=p^k < x\)，显然 \(y \mid f(x-1)\)。因此 \(1\sim x-1\) 中已经包含了这个最大指数，矛盾。

所以当且仅当 \(c=1\)，即 \(x\) 为质数的次幂时，满足 \(x \nmid f(x-1)\)。统计质数及质数次幂即可。

注意到 \(R-L \le 10^7\)，使用 Prime Distance 类似的筛法即可。

Day 4（2025.6.30）

AT_abc412_f

简述题意：给定 \(N\) 种颜色，每种颜色 \(i\) 有 \(A_i\) 只袜子。初始抽屉外有一只颜色 \(C\) 的袜子。每次操作随机抽取一只袜子，若颜色与抽屉外相同则终止，否则，放回一只袜子以最小化未来期望操作次数。求期望操作次数模 \(998244353\)。

最小化未来期望次数，可以感性地理解为让未来操作次数尽量小。

按照每种颜色袜子个数从小到大编号。那么每次相当于留下大的放回去小的。设总的袜子个数为 \(S+1\)。

期望问题通常上来说考虑 DP（即列式子）。

• 状态：

  • 发现每种颜色在外面是一种不同的、独立的子问题。因此定义 \(f_i\) 表示外面的颜色为 \(i\) 的拿的期望。

• 转移：

\[f_i=1+\sum_{k=1}^{i-1}\dfrac{A_k}{S}f_i+\sum_{k=i+1}^N\dfrac{A_k}{S}f_k \]

• 其中 \(1\) 表示取一次。考虑这一次取到了什么：

  • 如果取到 \(1\sim i-1\) 中的，那么保留 \(i\)。问题继续转化为外面的颜色为 \(i\)​。
  • 如果取到 \(i\)，那么直接停止了，没有后续问题，期望为 \(0\)​。
  • 如果取到 \(i+1\sim N\) 中的，那么保留这个颜色。问题转化为外面的颜色为 \(k\)。

• 移项化简可知：

\[f_i=\dfrac{1+\sum\limits_{k=i+1}^N\dfrac{A_k}{S}f_k}{1-\sum\limits_{k=1}^{i-1}\dfrac{A_k}{S}} \]

• 转移顺序与边界情况：
  • 显然从后往前转移。
  • 对于不合法和初始的情况，都赋为 \(0\) 即可。

做完，注意前缀和优化。

AT_abc411_e

简述题意：给你 \(n\) 个六面色子，你要求出同时掷出这些色子，掷出的面上数的最大值的期望。对 \(998244353\) 取模。

离散化，设共有 \(d\) 个不同的数，第 \(i\) 个是 \(S_i\)。

列出期望式子。最大值的情况数可以用“最多取到 \(x\) 减去最多取到 \(x-1\)”来计算。

\[\sum_{k=1}^d S_k(P(\le S_k)-P(\le S_{k-1})) \]

使用变换，将不好减的式子转化为好减的式子

\[s_k-\sum_{k=1}^{d-1}(s_{k+1}-s_k)P(\le S_k) \]

开 \(n\) 个指针维护即可。注意处理 \(0\) 的情况：有零，整个乘积都是 \(0\)。可以维护 \(0\) 的个数来解决。

Day 5（2025.7.1）

AT_abc410_g

简述题意：在一个圆上顺时针标记 \(2n\) 个点，给出 \(n\) 条不相交的弦 \((A_i,B_i)\)，每条弦连接两个不同的点。你可以选择若干条原有弦，使它们两两不相交。然后你可以额外添加一条任意的新弦。问操作后最多能有多少对弦相交。输出这个最大交点数。

考虑最终选出来的弦长什么样。

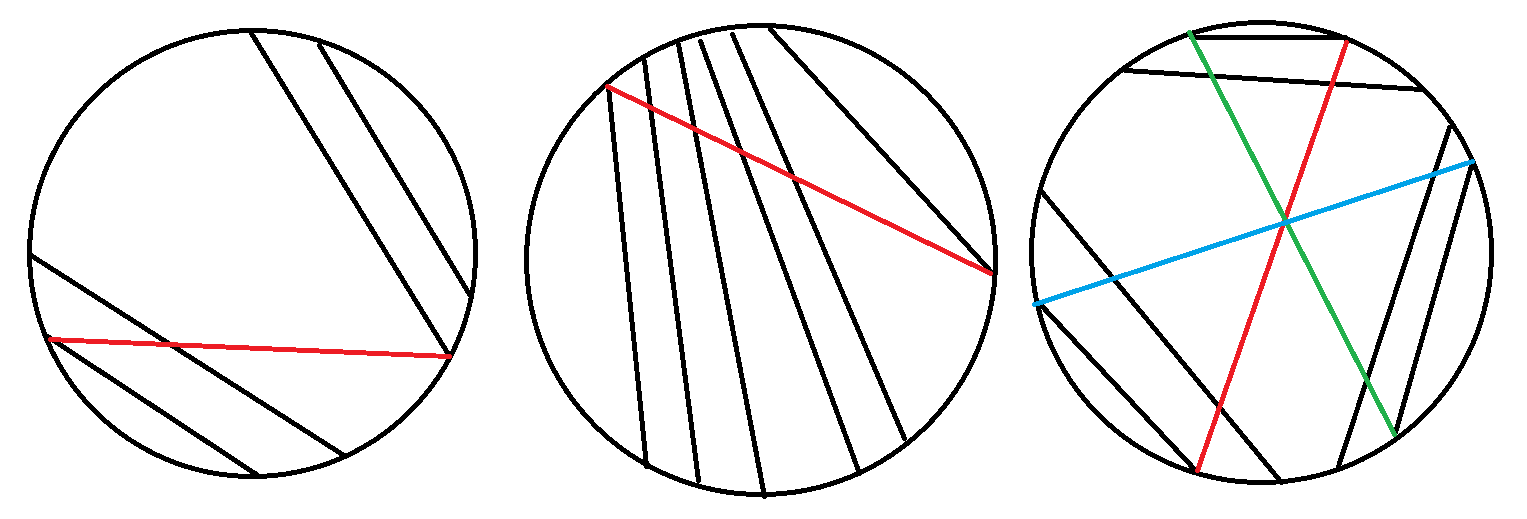
左边的（分成两部分）可以，中间的（一部分）可以，右边的（大于两部分）一条弦无法都进去，只能连两部分。

圈上问题考虑断圈成直线。于是直线大概长这样：（没有两部分的强行找到一个可以分成两部分的点去断就可以了）

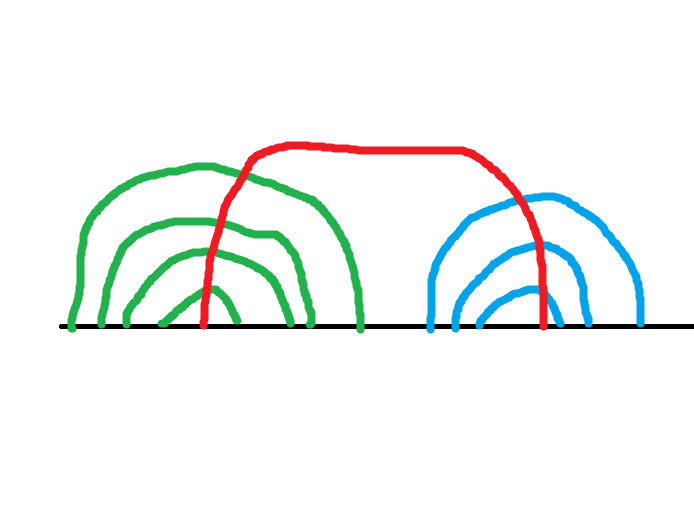
考虑对嵌套的层数作为状态进行 DP。

• 状态

  • \(f_i\) 表示线段 \(i\) 能够嵌套的最大层数。

  • 统计答案，由于蓝绿部分不能相较，考虑枚举蓝绿最上面那层的下标。\(ans=\max\limits_{j<i, B_j<A_i} f_j+f_i\)。

• 转移

  • 朴素地，\(f_i=\max\limits_{A_i<A_j<B_j<B_i}f_j+1\)。
  • 考虑消去一个维度的限制。不妨按照 \(B_i\) 升序排序所有弦，这样子方程化为 \(f_i=\max\limits_{A_i<A_j} f_j+1\)，发现答案式子不需修改。
  • 对于所有 \(A_i\) 树状数组维护最大的 \(f_i\) 即可。

• 边界与转移顺序

  • 顺序转移即可。
  • \(f\) 初始全部为 \(0\) 就行。

对于答案式子，由于我们对 \(B_i\) 升序排序了，所以动态地用第二个树状数组维护 \(\max\limits_{i=1}^x f_i\)。然后遍历 \(i\) 每次找出满足 \(B_j<A_i\) 的最大 \(j\)，树状数组查询即可。

Day 6（2025.7.2）

AT_abc386_c / AT_abc386_f

简述题意：给定两个字符串 \(S\) 和 \(T\)，以及一个整数 \(K\)。你可以对 \(S\) 执行最多 \(K\) 次操作，使其变为 \(T\)。每次操作可以是插入一个字符、删除一个字符或将一个字符替换成另一个字符。判断是否存在一种方式在进行不超过 \(K\) 次操作后

将 \(S\) 变为 \(T\)。

注意到操作次数为编辑距离。

注意到 \(f_{i,j} \le \left|i-j\right| \le k\)。对于 \(\left|i-j\right| > k\)，直接排掉就行。

令 \(g_{i,j-i}=f_{i,j}\)，暴力转移，做完。

AT_abc411_f

简述题意：给定一个无向图 \(G_0\)，有 \(N\) 个点 \(M\) 条边，第 \(i\) 条边连接点 \(U_i\) 和 \(V_i\)。每个点上初始放置一个编号为 \(1\) 到 \(N\) 的物品，第 \(i\) 个物品在第 \(i\) 个点上。接下来有 \(Q\) 次操作，每次给出一个边的编号 \(X_i\)，如果连接该边的两个点上放着不同的物品，则将该边收缩为一个新点（并移除自环、重边），两个物品合并到新点上。每次操作后，输出当前图中的边数。

分析合并后边数的变化。设原边数为 \(m'\)，则现边数 \(m=m'-1-s\)。其中 \(-1\) 是减去两点之间的边，\(s\) 表示两者共同的直接邻居（需要删去一条重边）。

注意到无向图中需要合并点的信息，考虑使用并查集启发式合并。对每个点维护一个数据结构（注意里面要保留的是结点的祖先编号而不是结点编号本身），暴力枚举计算即可。

AT_abc409_f

简述题意：初始图 \(G\) 有 \(N\) 个点和 \(0\) 条边，每个点有平面坐标，距离定义为曼哈顿距离。支持三种操作：一是添加一个新点，坐标为 \((a,b)\)；二是若当前图中联通块数量不少于 \(2\)，将所有距离最小的联通块之间连边并合并，输出该最小距离；若只有一个联通块，输出 \(-1\)；三是查询点 \(u\) 和 \(v\) 是否在同一个联通块中。

注意到操作二比较难操作，先考虑操作二。

分析数据范围，发现可以存下来每两点之间的边。

于是开一个堆，对于操作二每次弹出距离最小的边，然后判断是否处于同一分量，没有的话就合并，有的话就弹掉然后继续。

对于操作一，把新产生的边插入即可。对于操作三，在并查集中判断即可。做完。

AT_abc405_g

简述题意：给定一个长度为 \(N\) 的数组 \(A\)，有 \(Q\) 次查询。每次查询给出整数 \(L, R, X\)，求删除 \(A\) 的区间 \([L,R]\) 中所有大于等于 \(X\) 的数，然后对剩下的数任意重排。问可以得到多少个不同的序列 \(B\)，对 \(998244353\) 取模输出。

神秘的区间询问，加上 \(2.5 \times 10^5\) 的神秘数据范围，考虑使用莫队。

注意到需要进行下列操作：

• 单点修改某数出现次数 \(cnt_x\)
• 查询 \(\prod\limits_{i=1}^{x-1} \dfrac{1}{cnt_i!}\)
• 查询 \(\sum\limits_{i=1}^{x-1}cnt_i\)

发现可以使用类似树状数组的东西维护，但这是 \(O(n\sqrt n\log n)\)的。

注意到修改次数多达 \(O(n\sqrt n)\)​，查询次数少达 \(O(n)\)​ 次，考虑使用分块进行平衡复杂度。写一个 \(O(1)\)​ 修改 \(O(n)\)​ 查询的分块就做完了。

然后被这道**卡常题硬控 1h。

Day 7（2025.7.3）

AT_abc404_f

简述题意：有 \(N\) 个按钮，其中一个是获胜按钮，其余是失败按钮，按钮外观相同。游戏进行 \(T\) 轮，每轮流程如下：按钮被随机打乱顺序；你可以按 \(M\) 次按钮，可以重复按同一个按钮；你会得知当前为止累计按中获胜按钮的次数。若累计按中获胜按钮的次数不少于 \(K\)，则你获胜。求你在策略最优的情况下获胜的概率。

注意到可以使用 DP。

• 状态：

  • 观察到结束和游戏进行轮数和按下获胜按钮次数 \(f_{i,j}\) 表示进行到第 \(i\) 轮，按下了获胜按钮 \(j\) 次的概率。
  • 将 \(j > k\) 的情况归到 \(j=k\)​ 计算即可。
  • 答案为 \(ans=f_{t,k}\)。

• 转移：

  • 我们钦定一个按钮顺序：从前往后按 \(r\) 个，然后后面的不按。注意到这么钦定不会影响答案。

  • 我们发现我们还需要知道按的次数的具体方案（即把 \(m\)​ 分配）。注意到可以钦定按的次数从前往后单调不增。设方案集合为 \(S\)，其中的元素 \((c_1,c_2,c_3,\ldots,c_r) \in S\)（\(x\)​ 是最后一个非零的下标）

  • 注意到我们需要预处理 \(S\)。

  • 那么我们有：

    \[f_{i,j}\gets\dfrac{n-r}{n}f_{i-1,j}+\dfrac{1}{n}\sum_{k=1}^rf_{i-1,c_k-j} \]

    有 \(\dfrac{n-r}{n}\) 的概率没按到（因为获胜按钮在后 \(n-r\) 个），对于前面的 \(r\) 个，每个都有 \(\dfrac{1}{n}\) 的概率被按到。

• 边界与转移顺序

  • 转移直接正常转即可。
  • 边界条件：\(f_{0,0}=1\)，原因显然。

Day 8（2025.7.4）