KMP 算法学习笔记

KMP 字符串匹配算法

一个人最可悲的地方不在于失败，而在于失败后，不去尝试找回曾经的自己而是直接推倒重来。—— KMP

\(\mathtt{一些定义}\)

• \(s(i)\) 为字符串 \(s\) 从左往右第 \(i\) 个字符，\(s(l,r)\) 为 \(s\) 从左往右第 \(l\) 个字符到从左往右第 \(r\) 个字符所构成的子串。

  例：设 s="abcdefg"，则 \(s(2)\) 为 b，\(s(3,5)\) 为 cde。

• \(t\)（长度为 \(m\)）的最长前后缀长度的定义：使得 \(t(1,k)\) 与 \(t(m - k + 1, m)\) 相等的最大 \(k\)​​​​​​ 值。

• 长度为 \(j\) 的前缀指 \(s(1,j)\)，假设 \(s\) 长度为 \(k\)，则长度为 \(j\) 的后缀指 \(s(k - j + 1, k)\)。

• 本文代码如无特殊说明，默认已经执行过：

  cin >> (a + 1) >> (b + 1);
  n = strlen(a);
  m = strlen(b);
  

\(\mathtt{引入：抽象的暴力算法形式}\)

KMP 所解决的问题非常简单：给定主串 \(A\)，模式串 \(B\)，问 \(B\) 在 \(A\) 中：

• 出现了多少次？
• 出现在什么位置上？

这个问题暴力做非常简单，上代码：

for(int i = 1;i + m - 1 <= n;i++)
{
    bool ok = 1;
    for(int j = i;j <= i + m - 1;j++)
    {
        if(a[i] != b[j])
        {
            ok = 0;
            break;
        }
    }
    if(ok) /*在位置 i 上匹配到，进行处理*/
}

这个暴力做法很显然，基本上一看代码就知道它的作用，接下来我们对它进行一些改动，以便于为下文的 KMP 算法做铺垫。

改动一：把 \(i\) 改成指针的形式，并修改定义。

我们定义 \(i\) 不再是子串的第一个字符的位置，而是子串最后一个字符的位置。

int i = 0;
while(i <= n)
{
    if(i - m + 1 < 1) continue;
    bool ok = 1;
    for(int j = i - m + 1;j <= i;j++)
    {
        if(a[i] != b[j])
        {
            ok = 0;
            break;
        }
    }
    if(ok) /*在位置 i 上匹配到，进行处理*/
    i++;
}

改动二：把 \(j\) 也改成指针的形式，并修改定义

\(j\) 代表：\(a(i - j + 1,i)\) 与 \(b(1,j)\)​ 完全相等。

注意到此时我们就需要让 \(i\) 和 \(j\) 同步变化，也就是说，当 \(a(i + 1)\) 等于 \(b(j + 1)\) 时，\(i\) 和 \(j\) 各加上 \(1\)，这样子才能保持 \(i\) 和 \(j\) 的定义，建议手推一下以更好的理解。

int i = 0, j = 0;
while(i < n && j < m)
{
    if(a[i + 1] == b[j + 1])
    {
        i++;
        j++;
    }
    else
    {
        i = i + 2 - j;
        j = 0;
    }
    if(j == m)
    {
        /*在 i + 1 - m 上匹配到*/
        j = 0;
    }
}

算法流程大致如下：

• 如果 \(a(i + 1)\) 和 \(b(j + 1)\) 相等，说明可以继续匹配下去，各加上 \(1\)。
• 如果不相等，说明匹配不下去了，\(j\) 直接跳回 \(0\)，\(i\) 回到最开始的地方的下一位（也就是 \(i - j +1 +1 = i-j+2\)，因为你现在匹配了 \(j\) 位，跳回去就是 \(i -j + 1\)，它的下一位就是 \(i - j + 1+ 1\)）。
• 如果 \(j=m\)，说明匹配成功，将 \(j\) 设为 \(0\)，从当前的 \(i\) 开始继续匹配（因为很可能会匹配多次，从 \(i\)​ 开始是因为前面都已经匹配过了）。

这个算法的复杂度为 \(O(nm)\)，有点慢，慢在哪呢？

\(\mathtt{优化：KMP\ 算法}\)

这个时候 K、M、P 三个人站了出来：慢在让 \(i\) 直接跳回去！

他们说，本来前面就已经匹配了那么多，现在一匹配不下去就要舍弃前面所有的匹配成果重新再来，这也太浪费了！

怎么办？他们提出了一个大胆的想法：让 \(i\) 不跳。

你可能会说，\(i\) 不跳？那这样不就无法保证匹配了吗？

别急，你想想，\(i\) 动不了，我们是不是可以通过调整 \(j\)，来使得在 \(i\) 不变的前提下，其依旧满足呢？注意，\(j\) 调整后要尽量大哦。（如果小的话跟直接调成 \(0\)​ 就没啥区别了）

显然可以，这就是 KMP 算法的核心：通过调整 \(j\)，使得在 \(i\) 不变的前提下，\(i\) 和 \(j\)​ 依旧满足定义。

显然，\(j\) 一定是变小的，因为变大的话，无法保证匹配。（本来下一位就无法保证匹配了，现在你还变大，相当于给后面可能无法匹配的位置强行搞成匹配）

KMP 提出了一个 \(\text{next}(i)\) 数组，他发现，这个数组与 \(A\) 无关，它的基本定义为：

当第 \(i\) 位可以匹配，第 \(i + 1\) 位无法继续匹配时，在 \(j\) 继续符合定义，即 \(a(i - j + 1,i)\) 与 \(b(1,j)\) 完全相等的情况下，能调整到的最大的 \(j\) 是多少？

KMP 算法和上面所讲的暴力算法非常类似，过程如下：

• 如果 \(a(i + 1)\) 和 \(b(j + 1)\) 相等，说明可以继续匹配下去，各加上 \(1\)。
• 如果不相等，说明匹配不下去了，\(j\) 跳回 \(\text{next}(j)\)，\(i\) 不变。
• 如果 \(j=m\)，说明匹配成功，将 \(j\) 设为 \(\text{next}(j)\)（因为很可能会匹配多次）。

这里无非就是把“跳回 0”这个动作改成了“跳回 \(\text{next}(j)\)”，并让 \(i\) 保持不变，这样的好处就在于，匹配失败一个位不会立刻推倒重来，而是会跳到先前的一部继续匹配。

代码实现时需要注意：由于第二步 \(i\) 不变，因此可以进行一个小小的改动：

• 如果 \(a(i +1)\) 和 \(b(j + 1)\) 不相等，一直让 \(j=\text{next}(j)\)，直到 \(j = 0\)​ 或相等为止。

（下文都称 \(\text{next}\) 数组为 \(p\) 数组）

由于不相等时总是会回到第二步，相当于一个循环，因此这个改动是正确的，代码如下：

while(j > 0 && b[j + 1] != a[i + 1]) j = p[j];

综合其它两步，实现如下：

while(j > 0 && b[j + 1] != a[i + 1]) j = p[j];
if(a[i + 1] == b[j + 1])
{
    i ++;
    j++;
}
if(j == m)
{
    /*i - m + 1 上可以匹配到*/
    j = p[j];
}

是不是和暴力很相似？没错，KMP 和暴力的唯一不同就在于使用了 \(\text{next}\) 数组避免了反复推倒重来所带来的无谓的时间消耗。

最后注意到 i++ 可以放到代码的末尾，这样子我们就可以把代码简化成 for 循环了，但需要注意：\(j=m\) 时，匹配位置的 \(i\) 改之后会少掉一，因此答案就需要加上一个一，具体看代码：

int j = 0;
for(int i = 0;i < n;i++)
{
    while(j > 0 && b[j + 1] != a[i + 1]) j = p[j];
    if(a[i + 1] == b[j + 1]) j++;
    if(j == m)
    {
        /*i - m + 2 上可以匹配到*/
        j = p[j];
    }
}

问题又来了，\(\text{next}\) 数组怎么求呢？

\(\mathtt{next\ 数组的新定义}\)

看图说话：

\(\mathtt{next\ 数组的求法}\)

下文代码默认已经执行过：

strcpy(s, b);

我们不妨来举个例子：

\[\large{\mathtt{ABACABAB}} \]

我们刚刚已经证明，\(p_i\)​ 的定义为：

\(p_i\) 代表 \(s(1,i)\) 的最长前后缀的长度。

也就是说，我们要去获取 \(1\le i \le n\) 中 \(s(1,i)\) 这个子串的最长前后缀长度。

怎么求？我们可以一位一位地去求。具体地，不妨假设 \(s(1,i-1)\) 的最长前后缀长度为 \(j\)，也就是说当前匹配了 \(j\) 位的前后缀，那么如果 \(s(i) = s(j + 1)\)，\(s(1,i)\) 的最长前后缀的长度就是 \(j+1\)，如下图：

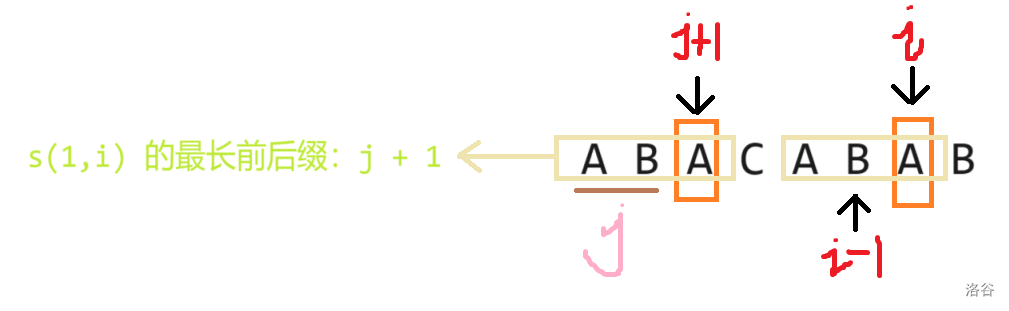
为了防止 \(i-1\) 下标越界，在写代码时，我们可以将上面的话换一种表达方式：设 \(s(1,i)\) 的最长前后缀长度为 \(j\)，那么如果 \(s(i + 1) = s(j + 1)\) ，\(s(1,i+1)\) 的最长前后缀的长度就是 \(j+1\)。写成代码大概长这样：

for(int i = 1;i < m;i++)
{
    if(s[i + 1] == s[j + 1]) j++;
    p[i + 1] = j;
}

那么如果不同呢？你想想，如果 \(s(i + 1) \neq s(j+1)\) ，那么是不是意味着我们就要重头再次开始匹配，也就是让 \(j = 0, i = 1\) 呢？当然不是！前面匹配了那么多肯定不能白费，既然前后缀长度为 \(j\) 无法继续匹配，那么我们就去找 \(s(1,j)\) 的最长前后缀。由于 \(s(1,j) = s(i - j + 1,i)\)，那么这个最长前后缀其实就是 \(s(1,j)\) 的前缀与 \(s(i - j + 1,i)\) 的后缀的不包括它们本身的最长公共串！（你可以把 \(s(i - j + 1,i)\) 的后缀看成是 \(s(1,j)\) 的后缀）那么既然它们是公共的，也就是说它就是前后缀（只不过不是最长的而已，是第二长，第一长是 \(s(1,j)\)）那么让 \(j\) 等于它继续匹配即可，因为它刚好是第二长，而又由于第一长匹配不下去，那么它继续匹配下去必然是最长前后缀。当然，如果第二长的也匹配不下去，那就换成第二长的最长前后缀，也就是第三长的继续匹配，理由同上。那么我们就只需要当下一位（\(s(i + 1)\) 和 \(s(j+1)\)）匹配不上时，不断地使 \(j=p(j)\)，找到可以匹配的那个 \(j\) 就可以啦！写成代码就是：

for(int i = 1;i < m;i++)
{
    while(j > 0 && s[i + 1] != s[j + 1]) j = p[j];
    if(s[i + 1] == s[j + 1]) j++;
    p[i + 1] = j;
}

然后 \(p\) 数组就被求出来啦！注意，\(j\) 的初值是 \(0\) 哦！

\(\mathtt{代码实现}\)

for(int i = 1;i < m;i++)
{
    while(j > 0 && s[i + 1] != s[j + 1]) j = p[j];
    if(s[i + 1] == s[j + 1]) j++;
    p[i + 1] = j;
}

int j = 0;
for(int i = 0;i < n;i++)
{
    while(j > 0 && b[j + 1] != a[i + 1]) j = p[j];
    if(a[i + 1] == b[j + 1]) j++;
    if(j == m)
    {
        /*i - m + 2 上可以匹配到*/
        j = p[j];
    }
}