【题解】Moving Dots 题解

$\mathtt{Problem\ Definition}$

题目讲得很抽象，这里直接上图说话：

$\mathtt{Solution}$

核心思想很简单，但是最难想到的就是核心思想，这个核心思想就是“正难则反”。

一些点移动停下来后不同坐标的个数本身就是一个非常抽象的数，如果直接进行统计并没有什么很好的方法，只能模拟。

那是否意味着这道题是不可做题呢？显然不是的，“正难则反”，我们可以从反面进行考虑。

我们发现，每个不同坐标肯定是两个点走到一起形成的（这很显然，因为与其它点重合就停止），那么我们可以考虑枚举点对 $(i,j)$，然后看看 $(i,j)$ 会在再选其它哪些点的情况之下能走到一起，那么这种选的情况的 $f$ 值就加一。最后所有点统计完之后，每个子集的 $f$ 都自然确定了，之后一加就完事。我们像这样，通过不同坐标反向计算 $f$。

这里还要注意一点：不用统计每个子集的 $f$，而是对于所有点对 $(i,j)$，把答案加上 $(i,j)$ 的“再选其它点的情况之下能走到一起”的选择方案数 $t$ 就行。原因的话就是因为有 $t$ 种选择其它点的方案，对于这 $t$ 种的每一个 $f$ 值都要加上 $1$，每次统计相当于给答案加上 $t$ 个 $1$，因此，就是给答案加上 $t$。

接着我们就来考虑求 $t$ 的值。

怎么求？“正难则反”，我们考虑不能选的点。

先来证明一个定理：

如果距 $x$ 最近的点是 $t$，那么若干时刻过后，距 $x$ 最近的点还是 $t$。

证明：不妨设距 $t$ 最近的点是 $y$，且 $x$ 在 $t$ 右侧。

• 若 $y$ 在 $t$ 左侧，则 $x,t$ 都往左走，由于速度相同，两者距离不变。

  设有其他点 $v$，如果 $v$ 往左走，同理距离不变，$t$ 距离最小。如果如果 $v$ 往左右走，距离则会增大，$t$ 距离依然最小。

• 若 $y$ 在 $t$ 右侧，$x$ 往左走，$t$ 往右走，两者距离缩短，依然最小。

  设有其他点 $v$，如果 $v$ 往左走，距离不变，$t$ 距离最小。如果如果 $v$ 往左右走，距离则会增大，$t$ 距离依然最小。

那么也就是说，一个点一旦出发，它的方向就是定的。

接着看图说话：

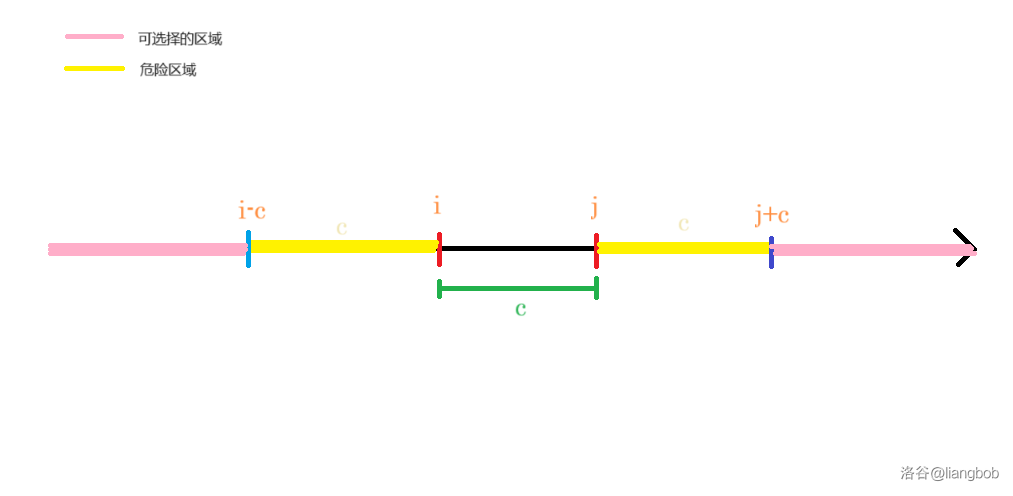
在左边黄色区域内，随便选一个点在里面都会把 $i$ “勾引”过去（因为它的距离比 $j$ 要小），根据上面的定理，而一旦勾引过去，就回不来了，因此左边黄色区域不能选点，为“危险区域”，右边黄色同理。那么自然而然，在粉色区域中，无论怎么选都不会勾引到任何一个点（因为距离都比 $j$ 要大），因此，$t$ 的值就是在粉色区域内乱选的方案数，为 $2^{t_1+t_2}$，其中 $t_1$ 为左边粉色区域点的个数，$t_2$ 为右边粉色区域点的个数。

问题又随之而来：$t_1$ 和 $t_2$ 又怎么算呢？这个就很简单了。我们给所有点排个序，然后二分找到最后一个（即下标最大的）小于 $i-c$ 的点，下标为 $p$；并同时二分找到第一个（下标最小的）大于等于 $j+c$ 的点，下标为 $q$。那么 $t_1=p$，$t_2=n-q+1$。

为什么 $t_1$ 是小于呢？因为由题意，当相邻两个距离都相同时，点总是会往左边走，那么你放在 $i-c$ 照样还是会被勾引，因此只能放在坐标比 $i-c$ 小的点。

$\mathtt{Code}$

详见 https://codeforces.com/contest/1788/submission/195932993。