斜率优化学习笔记

斜率优化是 dp 的一种有力优化方式。常用于处理当 dp 方程 \(f[i] = max(f[j]+ val(i, j))\) 中 \(val(i,j)\) 出现同时关于 \(i\),\(j\) 的项，而无法直接单调队列优化的情况。

引入

考虑这么一个问题：

• 你有一个长度为 \(N\) 的序列，每一位上都有一个数字。现在你要把这个序列分成若干段，一段的得分为 \(ax^2+bx+c\)，其中 \(x\) 是这一段内所有数字的和。现在请你求出这段序列各段得分之和的最大值。

• \(n \leq 5000, a < 0\)

显然的 dp 问题。令 \(f[i]\) 为以 \(i\) 为某一段的结尾，前面总得分的最大值。显然我们有状态转移方程：\(f[i] = max(f[j]+a \times (sum[i]-sum[j])^2 + b \times (sum[i]-sum[j])+c)\)，其中 \(sum[i]\) 是前缀和。

这样可以在 \(O(n^2)\) 解决这个问题，但如果数据范围加强到 \(n \leq 10^6\) 呢？

第一时间想起的可能是单调队列优化。我们知道，单调队列优化也是 \(O(n)\) 的复杂度。只要你能把 dp 方程中关于 \(i\) 的项和关于 \(j\) 的项分开就 ok 了。尝试对方程进行一系列变形（为了明显，我们把如上的 \(a,b,c\) 系数改成大写 \(A,B,C\)，先把 \(\max\) 去掉，后面再说）：

\(f[j]+Asum[j]^2-Bsum[j]+c=sum[j] \times 2Asum[i] + (Asum[i]^2-Bsum[i]+f[i])\)

我们发现，万事俱备，就是中间的那个 \(sum[j] \times 2Asum[i]\) 非常恼火——它是一个同时关于 \(i\) 和 \(j\) 的项——我们该怎么处理它呢？

至此，我们引出 dp 优化中一个非常重要的概念——「斜率优化」。

浅谈斜率优化

继续观察上式，你发现有什么特点？

我们令 \(y = f[j]+Asum[j]^2-Bsum[j]+c,x=sum[j]\)，把之前一个决策 \(j\) 的信息存储在一个二元组 \((x,y)\) 内。方程变为 —— \(y=2Asum[i] \times x + (Asum[i]^2-Bsum[i]+f[i])\)。

这像个什么？直线解析式！

可以想象，我们在一个平面直角坐标系上把 \(1 \sim i-1\) 的决策对应的二元组 \((x,y)\) 当成点的坐标撒下去，如下图：

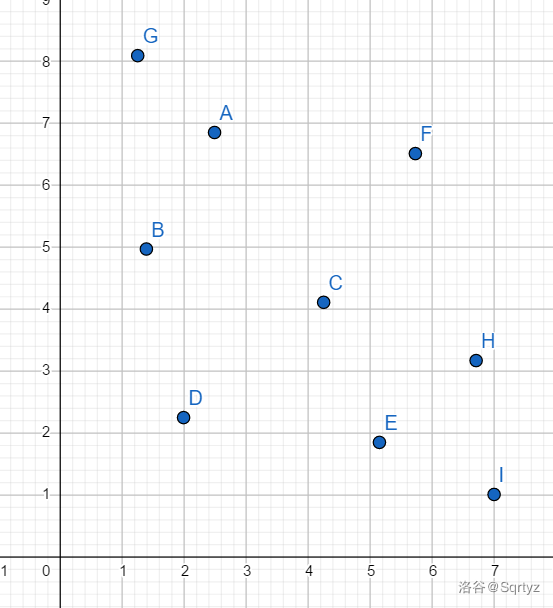
现在我们要得到一个正确的 \(f[i]\)，显然必须满足 \(y=2Asum[i] \times x + (Asum[i]^2-Bsum[i]+f[i])\) 这个等式（这毕竟原来是 \(f[i]\) 的推导公式）。

我们再把当前这个决策点 \(i\) 变成一条直线，一条斜率为 \(2Asum[i]\)，截距为 \(Asum[i]^2-Bsum[i]+f[i]\) 的直线（注意当前 \(f[i]\) 尚未确定，其他要素均已确定）。如果上面那个等式成立，是不是就说明——这条直线过 \((x,y)\) 这个点？那么 \(f[i]\) 就可以解出！

冷静一下，我们还有一个重大发现——我们要的是最大的 \(f[i]\) （前面移除了个 \(\max\) 还记得吗），也就是说这条直线的截距要尽量大！如下图：（注意由于 \(A<0\)，斜率小于 \(0\)）

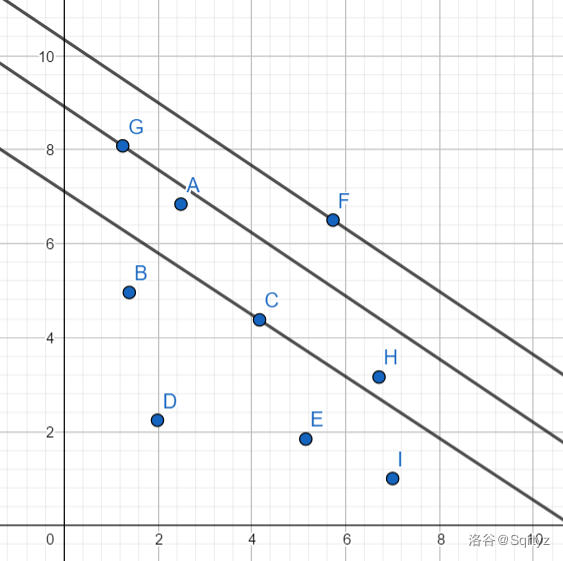
显然，过决策点 \(F\) 的直线截距最大，对应地，此时取得的 \(f[i]\) 最大。

我们现在要做的，就是使程序在均摊 \(O(1)\) 下找到这个点。

再次观察，哪些点是肯定无用的？

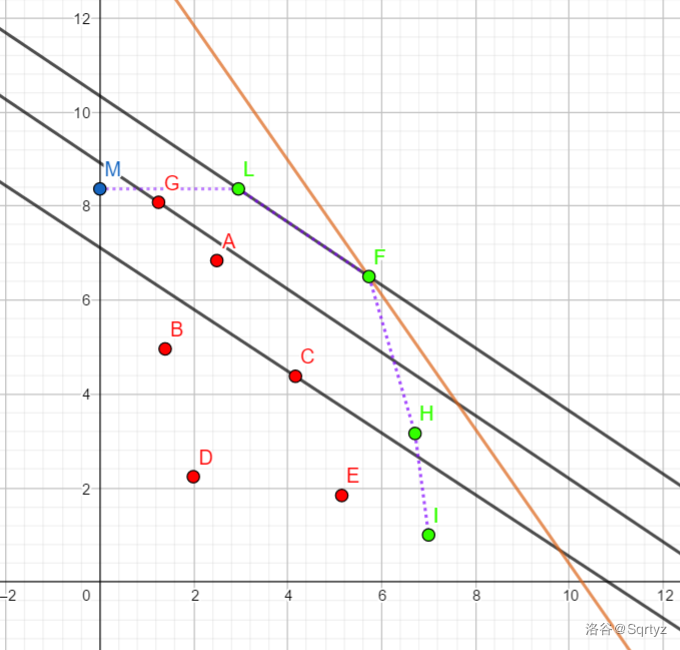
显然，红色点不可能取到，因为他们被圈在了一个紫色的边框内，这个边框叫做「凸包」。而我们现在要做的，就是维护这个「凸包」。

如何维护？首先我们发现，点的 \(x\) 坐标递增（回到定义看显然）。因此每次新加入的决策点都是在最右侧，我们判断它是在凸包上还是凸包内就 ok 了。

我们维护一个单调队列，左边靠队头，右边靠队尾。显然只有当队尾和在队尾左侧的那个点的斜率大于队尾和新加入的点的斜率（注意此时斜率为负），也就是这个新加入的决策点在凸包上，才不会影响之前的点。假如上图 I 是新增的决策，那么有 \(k_{FH}>k_{HI}\)，I 才能进来。否则，就要往前不断判断，把一些点弹出队列，直到 I 满足入队的要求（形成凸包）。

记得单调队列还要维护队头，这个也一样。观察到，假如队头和其下一个点的斜率大于当前决策 \(i\) 的斜率（注意此时斜率为负），队头就废了，因此我们也找到了出队的方法，如下图：

假如 \(i\) 增大，斜率会减小（回到定义，注意斜率为负），当其偏离至橙色的直线时，斜率小于了 \(k_{LF}\)（\(M\) 是辅助点，不用管，\(L\) 才是队头），此时显然 L 不能再被接下来的直线切到，因此 L 出队。

至此，斜率优化的全过程已经展示完毕。本题即为 [APIO2010] 特别行动队，参考代码如下：

#include <iostream>
#include <cstring>
#include <cstdio>

#define Maxn 1000010
#define LL long long

using namespace std;

int read() {
	int x = 0, f = 1;
	char c = getchar();
	while(c < '0' || c > '9') {
		if(c == '-') f = -1;
		c = getchar();
	}
	while('0' <= c && c <= '9') {
		x = x * 10 + c - '0';
		c = getchar();
	}
	return x * f;
}

LL N, A, B, C, sum[Maxn], f[Maxn], Q[Maxn];

double k(LL a, LL b) {
	LL xa = sum[a], ya = f[a] + A * sum[a] * sum[a] - B * sum[a] + C;
	LL xb = sum[b], yb = f[b] + A * sum[b] * sum[b] - B * sum[b] + C;
	return (yb - ya) * 1.0 / (xb - xa);
}

int main() {
	N = read();
	A = read(); B = read(); C = read();
	for(int i = 1; i <= N; ++i) sum[i] = read() + sum[i - 1];
	int head = 1, tail = 1;
	for(int i = 1; i <= N; ++i) {
		while(head < tail && k(Q[head], Q[head + 1]) > 2 * A * sum[i]) ++head;
		int j = Q[head];
		f[i] = f[j] + A * sum[j] * sum[j] - B * sum[j] + C - 2 * A * sum[j] * sum[i] + A * sum[i] * sum[i] + B * sum[i];
		while(head < tail && k(Q[tail - 1], Q[tail]) < k(Q[tail], i)) --tail;
		Q[++tail] = i;
	}
	cout << f[N] << endl;
	return 0;
}

例题与分析

[Luogu P2365] 任务安排

首先我们可以化出和之前类似的 dp 方程，如下：

\(f[j] = (S + t[i]) * c[j] + f[i] - t[i] * c[i] - S * c[N]\)

显然，决策点的坐标应为 \((c[j],f[j])\)，直线斜率为 \(S+t[i]\)，直接斜率优化 dp 即可。

需要注意的是，与上题不同的是，这道题维护的是下凸包。

代码如下：

#include <iostream>
#include <cstring>
#include <cstdio>

#define Maxn 5010

using namespace std;

int read() {
	int x = 0, f = 1;
	char c = getchar();
	while(c < '0' || c > '9') {
		if(c == '-') f = -1;
		c = getchar();
	}
	while('0' <= c && c <= '9') {
		x = x * 10 + c - '0';
		c = getchar();
	}
	return x * f;
}

int N, S, t[Maxn], c[Maxn], f[Maxn], Q[Maxn * 2];

double k(int a, int b) {
	return (f[b] - f[a]) * 1.0 / (c[b] - c[a]);
}

int main() {
	N = read(); S = read();
	for(int i = 1; i <= N; ++i) {
		t[i] = read() + t[i - 1];
		c[i] = read() + c[i - 1];
	}
	int head = 1, tail = 1;
	for(int i = 1; i <= N; ++i) {
		while(k(Q[head], Q[head + 1]) < S + t[i] && head < tail) ++head;
		f[i] = f[Q[head]] + t[i] * c[i] + S * c[N] - (S + t[i]) * c[Q[head]];
		while(k(Q[tail - 1], Q[tail]) > k(Q[tail], i) && head < tail) --tail;
		Q[++tail] = i;
	}
	cout << f[N] << endl;
	return 0;
} 

拓展

还是上面的题目，但如果 \(t_i\) 可能是负数，即查询的斜率不具有单调性，该怎么办呢？

思考一下，此时队尾出队仍和原来一样，因为插入的决策点的横坐标仍具有单调性。然而队头出队就不一定了，因为以前我们是根据斜率的单调来弹出队头的，现在斜率不再单调，队头也必须保存。

因此这样维护凸包的数据结构就是一个单调栈。当我们要查询的时候，由于斜率不单调，不能再直接读取队头，需要二分找到刚好直线切凸包的位置，复杂度只多了一个 \(\log\)。

此即 [SDOI2012]任务安排，下面呈现有关代码：

#include <iostream>
#include <cstring>
#include <cstdio>

#define Maxn 300010
#define LL long long

using namespace std;

int read() {
	int x = 0, f = 1;
	char c = getchar();
	while(c < '0' || c > '9') {
		if(c == '-') f = -1;
		c = getchar();
	}
	while('0' <= c && c <= '9') {
		x = x * 10 + c - '0';
		c = getchar();
	}
	return x * f;
}

LL N, S, t[Maxn], c[Maxn], f[Maxn], stack[Maxn * 2], top = 1;

double k(int a, int b) {
	return (f[b] - f[a]) * 1.0 / (c[b] - c[a]);
}

int ef(int l, int r, int i) {
	while(l < r) {
		int mid = (l + r) >> 1;
		if(f[stack[mid + 1]] - f[stack[mid]] <= (S + t[i]) * (c[stack[mid + 1]] - c[stack[mid]])) l = mid + 1;
		else r = mid;
	}
	return stack[l];
}

int main() {
	N = read(); S = read();
	for(int i = 1; i <= N; ++i) {
		t[i] = read() + t[i - 1];
		c[i] = read() + c[i - 1];
	}
	for(int i = 1; i <= N; ++i) {
		int j;
		if(top > 1) j = ef(1, top, i);
		else j = stack[1];
		f[i] = f[j] + t[i] *c[i] + S * c[N] - (S + t[i]) * c[j];
		while((f[stack[top]] - f[stack[top - 1]]) * (c[i] - c[stack[top]]) >= (f[i] - f[stack[top]]) * (c[stack[top]] - c[stack[top - 1]]) && top > 1) --top;
		stack[++top] = i;
	}
	cout << f[N] << endl;
	return 0;
}