DS博客作业04--图
0.PTA得分截图

1.本周学习总结
1.1 总结图内容
图的种类
按照边的类型分类
无向图:
任意两顶点之间的边都是无向边
无向图表示: G=(V , E )
顶点集合: V(G) = {V1,V2,V3,V4,V5)
边集:E(G) = { (V1,V2),(V1,V4),(V2,V3),(V2,V5),(V3,V4)}
有向图:
任意两顶点之间的边都是有向边
有向图表示: G=(V , E )
顶点集合: V(G) = {V1,V2,V3)
边集:E(G) = { <V1,V2>,<V1,V3>,<V2,V3>}
混合图:
有向边与无向边同时存在的图。
按照边上是否带有数值
有权图/网(Network):图的边或者弧有关联的数值
无权图:图的边或者弧有关联的数值
定义按照边数多少分类
稀疏图:有很少条边或弧(边数E远小于顶点数平方V^2)
稠密图:有很多条边或弧(边数E接近顶点数平方V^2)
其他
简单图:没有自环边没有平行边的图。
- 自环边:指向自己的边称为自环边。
- 平行边:两个节点之间的多条边成为平行边。
完全图:每对顶点之间都恰连有一条边的图
完全图通常使用,其中表示定点数
完全图属于简单图的特例。
多重图:含有平行边不含有自环边的图。
伪图:含有平行边和自环边的图。
二分图/二部图/偶图: 顶点可以分成两个不相交的集使得在同一个集内的顶点不相邻(没有共同边)的图。
图定义和基本术语
定义
图由顶点集V(G)和边集E(G)组成,记为G=(V,E)。其中E(G)是边的有限集合,边是顶点的无序对(无向图)或有序对(有向图)。对有向图来说,E(G)是有向边(也称弧(Arc))的有限集合,弧是顶点的有序对,记为<v,w><v,w>,v、w是顶点,v为弧尾(箭头根部),w为弧头(箭头处)。 对无向图来说,E(G)是边的有限集合,边是顶点的无序对,记为(v, w)或者(w, v),并且(v, w)=(w,v)。
基本术语
端点和邻接点:
在一个无向图中,若存在一条边(i,j),则称顶点i和顶点j为该边的两个端点,并称它们互为邻接点,即顶点i是顶点j的一个邻接点,顶点j是顶点i的一个邻接点,边(i,j)和边i,j关联。在一个有向图中,若存在一条有向边<i,j>,则称此边是顶点i的一条出边,同时也是顶点j的入边,i为此边的起始端点,j为此边的终止端点,顶点j是顶点i的出边邻接点,顶点i是顶点j的出边邻接点。
顶点的度、入度和出度:
在无向图中,一个顶点所关联的边的数目称为该顶点的度。在有向图中,顶点的度又分为人度和出度,以顶点j为终点的边数目,称为该顶点的入度。以顶点i为起点的边数目,称为该顶点的出度。一个顶点的入度与出度的和为该顶点的度。若一个图中有n个顶点和e条边,每个顶点的度为di(0≤i≤n-1),则有:e = 1/2Σdi(0≤i≤n-1)也就是说,一个图中所有顶点的度之和等于边数的两倍。因为图中的每条边分别作为两个邻接点的度各计一次。
完全图:
若无向图中的每两个顶点之间都存在着一条边,有向图中的每两个顶点之间都存在着方向相反的两条边,则称此图为完全图。 显然,无向完全图包含有n(n-1)/2条边,有向完全图包含有n(n-1)条边。
稠密面和稀疏面:
当一个图接近完全图称为稠密面,当一个图含有较少的边数(e<nlog2n),则称为稀疏面。
子图:
设有两个图G=(V,E)和G'=(V',E'),若V'是V的子集,则E'是E的子集,G'是G的子图
路径和路径长度:
在一个图中G=(V,E),从顶点i到顶点j的一条路径是一个顶点序列。路径长度是指一条路径上经过的边的数目。若一条路径上除开始点和结束点可以相同以外,其余顶点均不相同,则称此路径是简单路径。
回路或环:
若一条路径上的开始点与结束点为同一个顶点,则此路径被称为回路或环。开始点与结束点相同的简单路径被称为简单回路或简单环。
连通、连通图和连通分量:
在无向图G中,若从顶点i到顶点j有路径,则称顶点i和顶点j是连通的。若图G中的任意两个顶点都是连通的,则称G为连通图,否则称为非连通图。无向图G中的极大连通子图称为G的连通分量。连通图的连通分量只有一个(即本身),而非连通图有多个连通分量。
强连通图和强连通分量:
在有向图G中,若从顶点i到顶点j有路径,则称从顶点i到顶点j是连通的。若图G中的任意两个顶点i和j都连通,即从顶点i到顶点j和从顶点j到顶点i都存在路径,则称图G是强连通图。有向图G中的极大强连通子图称为G的强连通分量。强连通图只有一个强连通分量(即本身),非强连通图有多个强连通分量。
在一个非强连通图中找强连通分量的方法如下:
(1)在图中找有向环。
(2)扩展该有向环:如果某个顶点到该环中的任一顶点有路径,并且该环中的任一顶点到这个顶点也有路径,则加入这个顶点。
权和网:
图中的每一条边都可以附有一个对应的数值,这种与边相关的数值称为权,权可以表示从一个顶点到另一个顶点的距离或花费的代价,边上带有权的图称为带权图也称作网。
图的基本操作
图G中顶点v的第一个邻接点,不存在时返回 -1
int FirstAdjVex(MGraph&G, int v)
{
int i;
for (i = 0; i < G.vexnum; i++)
if (G.arcs[v][i].adj)
return i;
return -1;
}
图G中顶点v在w之后的下一个邻接点,不存在时返回 -1
int NextAdjVex(MGraph G, int v, int w)
{
int i;
for (i = w + 1; i < G.vexnum; i++)
if (G.arcs[v][i].adj)
return i;
return -1;
}
定位顶点
int LocateVex(MGraph &G, char v)
{
int i;
for (i = 0; i<G.vexnum; i++)
if (v == G.vers[i])
return i;
return -1;
}
创建有向图
void CreateMGraph(MGraph& g, int n, int e)//建图
{
int i, j;
int x, y;
for (i = 1; i <= n; i++)
{
visited[i] = 0;
for (j = 1; j <= n; j++)
g.edges[i][j] = 0;
}
for (i = 0; i < e; i++)
{
cin >> x >> y;
g.edges[x][y] = 1;
}
g.n = n;
g.e = e;
}
void CreateAdj(AdjGraph*& G, int n, int e)//创建图邻接表
{
int i;
int x, y;
ArcNode* p, * q;//因为是无向图所以要双向建立关系
G = new AdjGraph;
G->e = e;
G->n = n;
for (i = 0; i <= n; i++)
G->adjlist[i].firstarc = NULL;
for (i = 1; i <= e; i++)
{
cin >> x >> y;
p = new ArcNode;
p->adjvex = y;
p->nextarc = G->adjlist[x].firstarc;
G->adjlist[x].firstarc = p;
}
}
创建无向图
void CreateMGraph(MGraph& g, int n, int e)//建图
{
int i, j;
int x, y;
for (i = 1; i <= n; i++)
{
visited[i] = 0;
for (j = 1; j <= n; j++)
g.edges[i][j] = 0;
}
for (i = 0; i < e; i++)
{
cin >> x >> y;
g.edges[x][y] = 1;
g.edges[y][x] = 1;
}
g.n = n;
g.e = e;
}
void CreateAdj(AdjGraph*& G, int n, int e)//创建图邻接表
{
int i;
int x, y;
ArcNode* p, * q;//因为是无向图所以要双向建立关系
G = new AdjGraph;
G->e = e;
G->n = n;
for (i = 0; i <= n; i++)
G->adjlist[i].firstarc = NULL;
for (i = 1; i <= e; i++)
{
cin >> x >> y;
p = new ArcNode;
q = new ArcNode;
q->adjvex = x;
p->adjvex = y;
p->nextarc = G->adjlist[x].firstarc;
G->adjlist[x].firstarc = p;
q->nextarc = G->adjlist[y].firstarc;
G->adjlist[y].firstarc = q;
}
}
计算图顶点的入度
void inDegree(AdjGraph g)
{
Node *p;
int i, inD;
int inD[g.n];//再初始化为0
for(i = 0; i < g.n; i++)
{
p = g.adj[i].first;
while(NULL != p)
{
inD[p->index]++;
p = p->next;
}
}
}
void inDegree(MatGraph g)
{
int i, j, inD;
for(j = 0; j < g.n; j++) // 列
{
inD = 0;
for(i = 0; i < g.n; i++) // 行
if(0 != g.edge[i][j])
inD++;
cout << "顶点" << j << "的入度为:" << inD << endl;
}
}
计算图顶点的出度
{
void outDegree(AdjGraph g)
{
Node *p;
int i, outD;
for(i = 0; i < g.n; i++)
{
outD = 0;
p = g.adj[i].first;
while(NULL != p)
{
outD++;
p = p->next;
}
cout << "顶点" << i << "的出度为:" << outD << endl;
}
}
void outDegree(MatGraph g)
{
int i, j, outD;
for(i = 0; i < g.n; i++) // 行
{
outD = 0;
for(j = 0; j < g.n; j++) // 列
if(0 != g.edge[i][j])
outD++;
cout << "顶点" << j << "的出度为:" << outD << endl;
}
}
图存储结构
邻接矩阵存储结构
图的邻接矩阵是一种采用邻接矩阵数组表示顶点之间相邻关系的储存结构。
邻接矩阵的特点:
(1)图的邻接矩阵表示是唯一的。
(2)对于含有n个顶点的图,采用邻接矩阵储存时,无论是有向图还是无向图,无论边的数目大小,其存储空间都为O(n*n),所以邻接矩阵适合于存储边的数目较多的稠密图。
(3)无向图的邻接矩阵数组一定是一个对称矩阵,因此储存时可以压缩,只需存放上三角或者下三角
(4)对于无向图,邻接矩阵数组的第i行或者第i列非零元素、非∞元素的个数正好是顶点i的度
(5)对于有向图,邻接矩阵数组的第i行(第i列)非零元素、非∞元素的个数正好是顶点i的出度(入度)
(6)在邻接矩阵中,判断图中两个顶点之间是否有边或者求两个顶点之间边的权的执行时间为0(1)。所以在需要提取边权值的算法中通常采用邻接矩阵存储结构。
typedef struct
{
int no; //顶点编号
int info; //顶点其他信息
}VertexType;
typedef struct //图的定义
{
int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,弧数
VertexType vexs[MAXV]; //存放顶点信息
} MGraph;
邻接表存储结构
图的邻接表(adjacencylist)是一种顺序与链式存储相结合的存储方法。对于含有n个顶点的图,每个顶点建立一个单链 表,第i(0≤i≤n-1)个单链表中的结点表示关联于顶点i的边(对有向图是以顶点i为起点的边),也就是将顶点i的所有邻接点(对有向图是出边邻接点)链接起来,其中每个结点表示一条边的信息。每个单链表再附设一个头结点,并将所有头结点构成一个头结点数组adjlist,adjlist[i]表示顶点i的单链表的头结点,这样就可以通过顶点i快速地找到对应的单链表。在邻接表中有两种类型的结点,一种是头结点,其个数恰好为图中顶点的个数;另-种是边结点,也就是单链表中的结点。 对于无向图,这类结点的个数等于边数的两倍;对于有向图,这类结点的个数等于边数。
边结点和头结点的结构如下:

其中,边结点由3个域组成,adjivex表示与顶点i邻接的顶点编号,nextarc指向下一个边结点,weight存储与该边相关的信息,如权值等。头结点由两个域组成,data存储顶点i的名称或其他信息firstar指向顶点i的单链表中的首结点。
邻接表的特点:
(1)邻接表的表示不唯一,这是因为在每个顶点对应的单链表中各边结点的链接次序可以是任意的,取决于建立邻接表的算法以及边的输入次序。
(2)对于有n个顶点和e条边的无向图,其邻接表有n个头结点和2e个边结点;对于有n个顶点和e条边的有向图,其邻接表有n个头结点和e个边结点。显然,对于边数目较少的稀疏图,邻接表比邻接矩阵更节省存储空间。
(3)对于无向图,邻接表中顶点i对应的第i个单链表的边结点数目正好是顶点i的度
(4)对于有向图,邻接表中顶点i对应的第i个单链表的边结点数目仅仅是顶点i的出度。顶点i的人度为邻接表中所有adjvex域值为i的边结点数目。
(5)在邻接表中,查找顶点i关联的所有边是非常快速的,所以在需要提取某个顶点的所有邻接点的算法中通常采用邻接表存储结构。
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{ AdjList adjlist; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
十字链表存储结构
十字链表存储有向图(网)的方式与邻接表有一些相同,都以图(网)中各顶点为首元节点建立多条链表,同时为了便于管理,还将所有链表的首元节点存储到同一数组(或链表)中。十字链表实质上就是为每个顶点建立两个链表,分别存储以该顶点为弧头的所有顶点和以该顶点为弧尾的所有顶点。
头结点:

firstin 指针用于连接以当前顶点为弧头的其他顶点构成的链表;
firstout 指针用于连接以当前顶点为弧尾的其他顶点构成的链表;
data 用于存储该顶点中的数据;
边结点:

tailvex 用于存储以首元节点为弧尾的顶点位于数组中的位置下标;
headvex 用于存储以首元节点为弧头的顶点位于数组中的位置下标;
hlink 指针:用于链接下一个存储以首元节点为弧头的顶点的节点;
tlink 指针:用于链接下一个存储以首元节点为弧尾的顶点的节点;
info 指针:用于存储与该顶点相关的信息,例如量顶点之间的权值;
typedef struct ArcBox{
int tailvex,headvex;//弧尾、弧头对应顶点在数组中的位置下标
struct ArcBox *hlik,*tlink;//分别指向弧头相同和弧尾相同的下一个弧
InfoType *info;//存储弧相关信息的指针
}ArcBox;
typedef struct VexNode{
VertexType data;//顶点的数据域
ArcBox *firstin,*firstout;//指向以该顶点为弧头和弧尾的链表首个结点
}VexNode;
typedef struct {
VexNode xlist[MAX_VERTEX_NUM];//存储顶点的一维数组
int vexnum,arcnum;//记录图的顶点数和弧数
}OLGraph;
int LocateVex(OLGraph * G,VertexType v){
int i=0;
//遍历一维数组,找到变量v
for (; i<G->vexnum; i++) {
if (G->xlist[i].data==v) {
break;
}
}
//如果找不到,输出提示语句,返回 -1
if (i>G->vexnum) {
printf("no such vertex.\n");
return -1;
}
return i;
}
//构建十字链表函数
void CreateDG(OLGraph *G){
//输入有向图的顶点数和弧数
scanf("%d,%d",&(G->vexnum),&(G->arcnum));
//使用一维数组存储顶点数据,初始化指针域为NULL
for (int i=0; i<G->vexnum; i++) {
scanf("%d",&(G->xlist[i].data));
G->xlist[i].firstin=NULL;
G->xlist[i].firstout=NULL;
}
//构建十字链表
for (int k=0;k<G->arcnum; k++) {
int v1,v2;
scanf("%d,%d",&v1,&v2);
//确定v1、v2在数组中的位置下标
int i=LocateVex(G, v1);
int j=LocateVex(G, v2);
//建立弧的结点
ArcBox * p=(ArcBox*)malloc(sizeof(ArcBox));
p->tailvex=i;
p->headvex=j;
//采用头插法插入新的p结点
p->hlik=G->xlist[j].firstin;
p->tlink=G->xlist[i].firstout;
G->xlist[j].firstin=G->xlist[i].firstout=p;
}
}
邻接多重表存储结构
邻接多重表存储无向图的方式,可看作是邻接表和十字链表的结合。同邻接表和十字链表存储图的方法相同,都是独自为图中各顶点建立一张链表,存储各顶点的节点作为各链表的首元节点,同时为了便于管理将各个首元节点存储到一个数组中。
头结点:

data:存储此顶点的数据;
firstedge:指针域,用于指向同该顶点有直接关联的存储其他顶点的节点。
边结点:

mark:标志域,用于标记此节点是否被操作过,例如在对图中顶点做遍历操作时,为了防止多次操作同一节点,mark 域为 0 表示还未被遍历;mark 为 1 表示该节点已被遍历;
ivex 和 jvex:数据域,分别存储图中各边两端的顶点所在数组中的位置下标;
ilink:指针域,指向下一个存储与 ivex 有直接关联顶点的节点;
jlink:指针域,指向下一个存储与 jvex 有直接关联顶点的节点;
info:指针域,用于存储与该顶点有关的其他信息,比如无向网中各边的权;
typedef enum {unvisited,visited}VisitIf; //边标志域
typedef struct EBox{
VisitIf mark; //标志域
int ivex,jvex; //边两边顶点在数组中的位置下标
struct EBox * ilink,*jlink; //分别指向与ivex、jvex相关的下一个边
InfoType *info; //边包含的其它的信息域的指针
}EBox;
typedef struct VexBox{
VertexType data; //顶点数据域
EBox * firstedge; //顶点相关的第一条边的指针域
}VexBox;
typedef struct {
VexBox adjmulist[MAX_VERTEX_NUM];//存储图中顶点的数组
int vexnum,degenum;//记录途中顶点个数和边个数的变量
}AMLGraph;
图遍历及应用
图遍历
| 深度优先搜索(DFS) |
算法思想:假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
算法特点:深度优先搜索是一个递归的过程。首先,选定一个出发点后进行遍历,如果有邻接的未被访问过的节点则继续前进。若不能继续前进,则回退一步再前进,若回退一步仍然不能前进,则连续回退至可以前进的位置为止。重复此过程,直到所有与选定点相通的所有顶点都被遍历。深度优先搜索是递归过程,带有回退操作,因此需要使用栈存储访问的路径信息。当访问到的当前顶点没有可以前进的邻接顶点时,需要进行出栈操作,将当前位置回退至出栈元素位置。
算法分析:当图采用邻接矩阵存储时,由于矩阵元素个数为n2,因此时间复杂度就是O(n2)。当图采用邻接表存储时,邻接表中只是存储了边结点(e条边,无向图也只是2e个结点),加上表头结点为n(也就是顶点个数),因此时间复杂度为O(n+e)。
邻接矩阵的DFS
void DFS(MGraph g, int v)//深度遍历
{
int i;
if (flag == 0)
{
cout << v;
flag = 1;
}
else
cout << " " << v;
visited[v] = 1;
for (i = 1; i <= g.n; i++)
{
if (visited[i] == 0 && g.edges[v][i] == 1)
DFS(g, i);
}
}
邻接表的DFS
void DFS(AdjGraph* G, int v)//v节点开始深度遍历
{
ArcNode* p;
visited[v] = 1;
if (flag == 0)
{
cout << v;
flag = 1;
}
else
cout << " " << v;
p = G->adjlist[v].firstarc;
while (p != NULL)
{
if (visited[p->adjvex] == 0)
DFS(G, p->adjvex);
p = p->nextarc;
}
}
| 广度优先搜索(BFS) |
算法思想:从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。
算法特点:广度优先搜索类似于树的层次遍历,是按照一种由近及远的方式访问图的顶点。在进行广度优先搜索时需要使用队列存储顶点信息。
算法分析:假设图有V个顶点,E条边,广度优先搜索算法需要搜索V个节点,时间消耗是O(V),在搜索过程中,又需要根据边来增加队列的长度,于是这里需要消耗O(E),总得来说,效率大约是O(V+E)。
邻接矩阵的BFS
void BFS(MGraph g, int v)//广度遍历
{
int num[100];
int index = 0, i;
if (flag == 1)
{
cout << v;
flag = 0;
}
visited[v] = 1;
for (i = 1; i <= g.n; i++)
{
if (visited[i] == 0 && g.edges[v][i] == 1)
{
num[index] = i;
index++;
visited[i] = 1;
cout << " " << i;
}
}
for (i = 0; i < index; i++)
BFS(g, num[i]);
}
邻接表的BFS
void BFS(AdjGraph* G, int v) //v节点开始广度遍历
{
ArcNode* p;
queue<int> q;
int i, num;
cout << v;
q.push(v);
visited[v] = 1;
while (!q.empty())
{
num = q.front();
q.pop();
p = G->adjlist[num].firstarc;
while (p != NULL)
{
if (visited[p->adjvex] == 0)
{
cout << " " << p->adjvex;
visited[p->adjvex] = 1;
q.push(p->adjvex);
}
p = p->nextarc;
}
}
}
应用
求一条包含所有顶点的回路
汉密尔顿(Hamilton)问题。起点的选择和顶点的邻接顺序会影响该简单路径是否能被找到;
修改DFS算法:访问顶点时将该顶点序号加入数组path[ ],n++判断是否所有顶点已被访问;某顶点所有邻接点全部被访问后回溯,计数器n--;
void DFS(MGraph &G, int i, int path[], int visited[], int &n) {
int j;
visited[i]=1;
path[n]=i;
n++;
if (n==G.vexNum) { // 符合条件输出路径
for (j=0; j<G.vexNum; j++) {
printf("%d", path[j]);
}
putchar('\n');
//return;
}
for (j=0; j<G.vexNum; j++) {
if (G.arcs[i][j]==1 && !visited[j]) {
DFS(G, j, path, visited, n);
}
}
visited[i] = 0;
n--;
}
void Hamilton(MGraph G) {
int i, n=0; //n记录当前该路径上的顶点数
int path[G.vexNum];
int visited[G.vexNum];
for (i=0; i<G.vexNum; i++) {
visited[i] = 0;
}
for (i=0; i<G.vexNum; i++) {
path[i] = INFINITY;
}
for (i=0; i<G.vexNum; i++) {
if (!visited[i]) {
DFS(G, i, path, visited, n); //i为起始点,n为加入路径的顶点个数
}
}
}
判断图中是否存在环
在图的深度遍历过程中,若出现与某个顶点有邻接关系的所有顶点均被访问过,则一定出现了回路。
修改DFS算法:对顶点x做深度优先遍历时,先计算其度dx和与它有邻接关系的访问标志数v;若dx==v,则出现回路,否则继续。
int DFS(MGraph &G, int i, int visited[]) {
int j, vi, di;
visited[i] = 1;
for (di = 0, vi = 0, j = 0; j<G.vexNum; j++) {
if (G.arcs[i][j]==1) {
di++;
if (visited[j]) {
vi++;
}
}
}
if (di == vi && di!=1) {
printf("有回路!\n");
return 1;
}
for (j=0; j<G.vexNum; j++) {
if (G.arcs[i][j]==1 && !visited[j]) {
if (DFS(G, j, visited)) {
return 1;
} else {
return 0;
}
}
}
printf("无回路!\n");
return 0;
}
求无向图的顶点a到i之间的简单路径
深度遍历过程中将所有访问到的顶点下标计入数组path[ ],若找到i顶点,则path中存储的即为a到i的简单路径;若未找到,删除path[ ]中的一个下标,回退,直至找到i。
void Append(int path[], int i);
void Delete(int path[]);
void DFSearchPath(MGraph G, int v, int w, int path[], int visited[], int &found) {
int j;
Append(path, v);
visited[v] = 1;
for (j=0; j<G.vexNum && !found; j++) {
if (G.arcs[v][j]==1 && !visited[j]) {
if (j == w) {
found=1;
Append(path, j);
}
DFSearchPath(G, j, w, path, visited, found);
}
}
if (!found) {
Delete(path);
}
}
求无向图的顶点A、B之间的最短路径
从源点进行BFS,让进入队列的节点既能完成按层遍历,又能记住路径;将队列节点修改为带prior指针指向该节点前驱;
对队列的操作修改:
typedef struct node{
int data;
struct node *prior, *next;
}QNode;
typedef struct {
QNode *fron, *reer;
}Queue;
void initQueue(Queue &Q) {
Q.fron = Q.reer = new QNode;
Q.fron->prior = Q.fron->next = NULL;
}
void enterQueue(Queue &Q, int data) {
Q.reer->next = new QNode;
Q.reer = Q.reer->next;
Q.reer->data = data;
Q.reer->next = NULL;
Q.reer->prior = NULL;
}
void deleQueue(Queue &Q) {
Q.fron = Q.fron->next;
}
算法实现:
void BFSearch(MGraph G, Queue &Q, int vi, int vj, int visited[]) {
int a, i;
enterQueue(Q, vi);
visited[vi] = 1;
while (Q.fron != Q.reer) {
a = Q.fron->next->data;
deleQueue(Q);
for (i=0; i<G.vexNum; i++) {
if (G.arcs[a][i] == 1 && visited[i]==0) {
enterQueue(Q, i);
Q.reer->prior = Q.fron;
visited[i] = 1;
if (i==vj) {
return;
}
}
}
}
}
void creatGraph(MGraph &G) {
int i, j, from, to;
//initial Graph
for(i=0; i<MAXSIZE; i++) {
for(j=0; j<MAXSIZE; j++) {
if(i == j) {
G.arcs[i][j] = 0;
continue;
}
G.arcs[i][j] = INFINITY;
}
}
printf("Please input verNum & arcNum\n");
scanf("%d%d", &G.vexNum, &G.arcNum);
printf("Please input vertices' name\n");
getchar();
for(i=0; i<G.vexNum; i++) {
scanf("%c", &G.vexs[i]);
}
printf("Please input edge\n");
for(i=0; i<G.arcNum; i++) {
scanf("%d%d", &from, &to);
G.arcs[from][to] = 1;
G.arcs[to][from] = 1;
}
}
最小生成树相关算法(Kruskal算法(克鲁斯卡算法)、Prim算法(普里姆算法)、Sollin(Boruvka)算法)及应用
生成树 (Spanning Tree):无向连通图G的一个子图如果是一颗包含G的所有顶点的树,则该子图称为G的生成树。生成树是连通图的极小连通子图。这里所谓极小是指:若在树中任意增加一条边,则将出现一条回路;若去掉一条边,将会使之变成非连通图。
最小生成树(Minimum Spanning Tree,MST):或者称为最小代价树Minimum-cost Spanning Tree:对无向连通图的生成树,各边的权值总和称为生成树的权,权最小的生成树称为最小生成树。
构成生成树的准则有三条:
<1> 必须只使用该网络中的边来构造最小生成树。
<2> 必须使用且仅使用n-1条边来连接网络中的n个顶点
<3> 不能使用产生回路的边。
相关算法
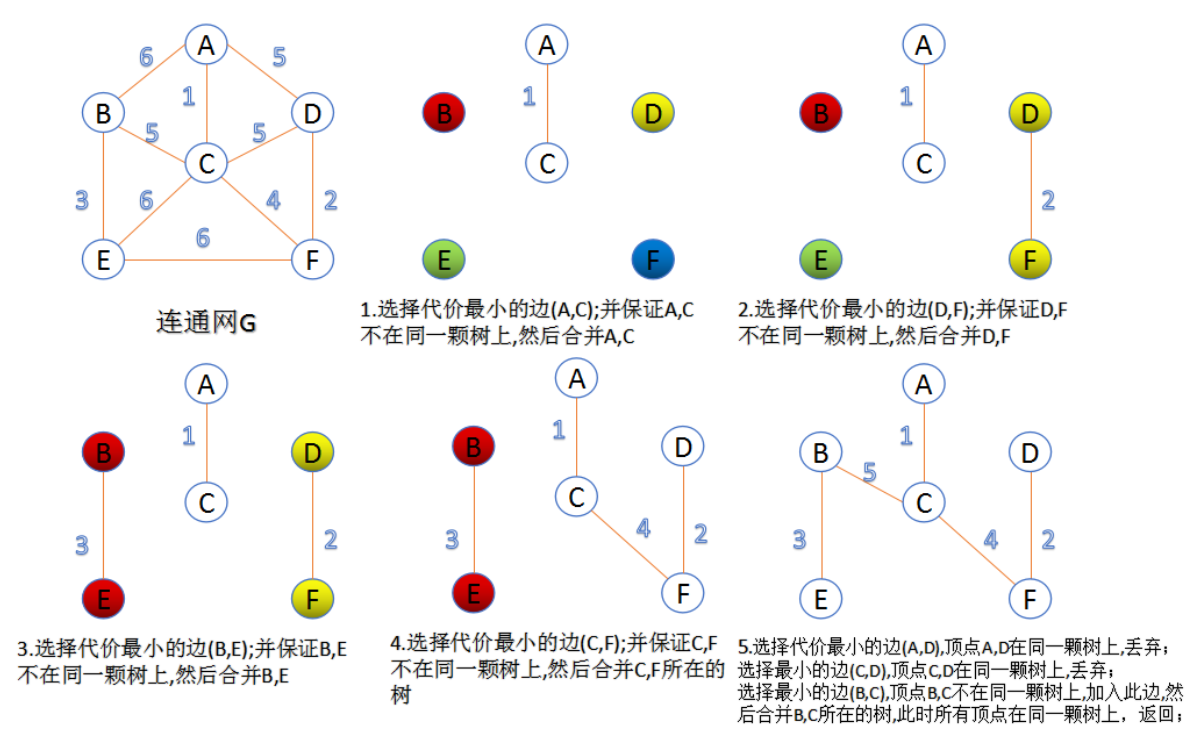
| Kruskal算法(克鲁斯卡算法) |
typedef struct
{
int u; //边的起始顶点
int v; //边的终止顶点
int w; //边的权值
}Edge;
void Kruskal(AdjGraph *g)
{
int i,j,u1,v1,sn1,sn2,k;
int vest[MAXV]; //集合辅助数组
Edge E[MAXV]; //存放所有边
k=0;//E数组的下标从0开始计
for(i=0;i<g.n;i++)
{
p=g->adjlist[i].firstarc;
while(p!=NULL)
{
E[k].u=i;E[k].v=p->adjvex;E[k].w=p->weight;
k++;
p=p->nextarc;
}
}
Sort(E,g.e);//用快排对E数组按权值递增排序
for(i=0;i<g.n;i++)
vest[i]=
k=1;//k表示当前构造生成树的第几条边,初值为1
j=0;//E的边的下标,初值为0
while(k<g.n)
{
u1=E[j].u;v1=E[j].v;sn1=vest[u1];sn2=vest[v1];
k++;
if(sn1!=sn2)
{
for(i=0;i<g.n;i++)
if(vest[i] == sn2)
vest[i]=sn1;
}
j++;
}
}
采用并查集
typedef struct _node
{
intval; //长度
int start; //边的起点
int end; //边的终点
}Node;
void make_set() //初始化集合,让所有的点都各成一个集合,每个集合都只包含自己
{
for(inti = 0; i < N; i++)
{
father[i] = i;
cap[i] = 1;
}
}
int find_set(int x) //判断一个点属于哪个集合,点如果都有着共同的祖先结点,就可以说他们属于一个集合
{
if(x != father[x])
{
father[x] = find_set(father[x]);
}
returnfather[x];
}
void Union(int x, int y) //将x,y合并到同一个集合
{
x = find_set(x);
y = find_set(y);
if(x == y)
return;
if(cap[x] < cap[y])
father[x] = find_set(y);
else
{
if(cap[x] == cap[y])
cap[x]++;
father[y] = find_set(x);
}
}
int Kruskal(int n)
{
int sum = 0;
make_set();
for(inti = 0; i < N; i++)//将边的顺序按从小到大取出来
{
if(find_set(V[i].start) != find_set(V[i].end)) //如果改变的两个顶点还不在一个集合中,就并到一个集合里,生成树的长度加上这条边的长度
{
Union(V[i].start, V[i].end); //合并两个顶点到一个集合
sum += V[i].val;
}
}
return sum;
}
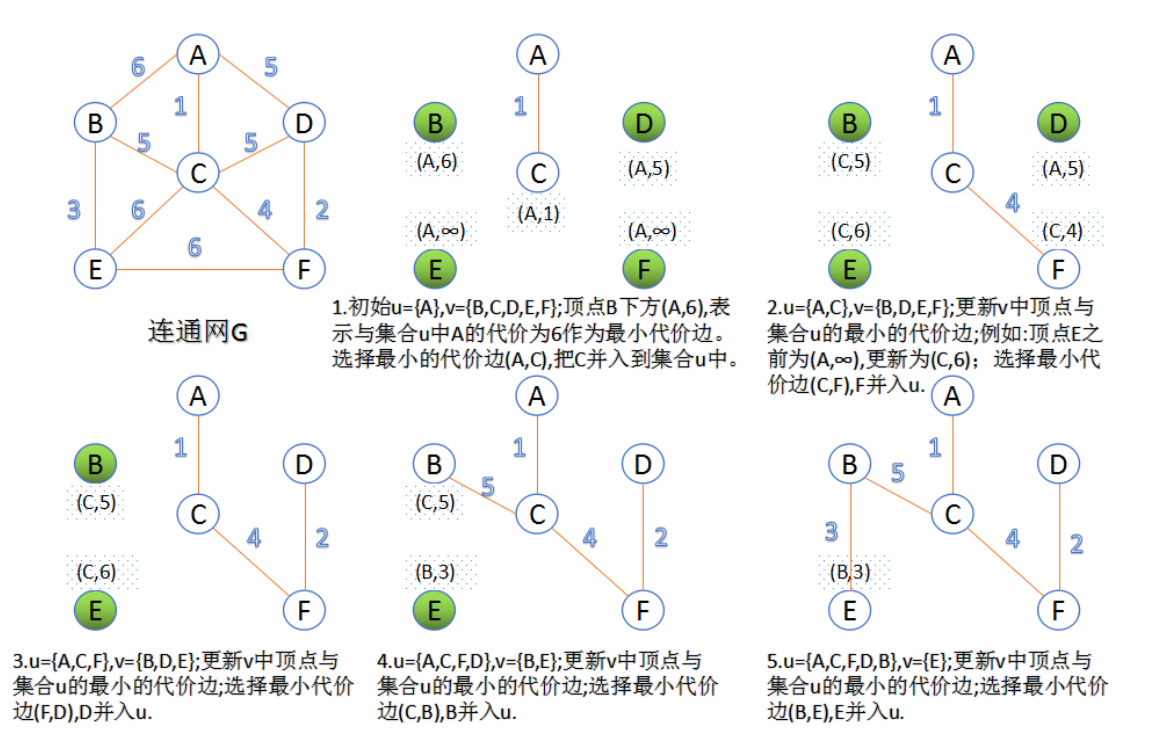
| Prim算法 |
void Prim(MGraph *G, int v)
{
int min = 32767, lowcost[1001], closest[1001], i, j, index;
int sum = 0, flag = 0;
for (i = 1; i <= G->n; i++)
{
lowcost[i] = G->edges[v][i];
closest[i] = v;
}
for (i = 1; i < G->n; i++)
{
min = 32767;
for (j = 1; j <= G->n; j++)
{
if (lowcost[j] != 0 && lowcost[j] < min)
{
min = lowcost[j];
index = j;
}
}
lowcost[index] = 0;
for (j = 1; j <= G->n; j++)
{
if (lowcost[j] != 0 && G->edges[index][j] < lowcost[j])
{
lowcost[j] = G->edges[index][j];
closest[j] = index;
}
}
}
}
| Sollin(Boruvka)算法 |
/*
nn存储每个分量的最邻近,a存储尚未删除且还没在MST中的边
*h用于访问要检查的下一条边
*N用于存放下一步所保存的边
*每一步都对应着检查剩余的边,连接不同分量的顶点的边被保留在下一步中
*最后每一步将每个分量与它最邻近的分量合并,并将最近邻边添加到MST中
*/
typedef struct{int v;int w;double wt;}Edge;
typeder struct{int V;int E;double **adj}Graph;
Edge nn[maxE],a[maxE];
void Boruvka(Graph g,Edge mst[])
{
int h,i,j,k,v,w,N;
Edge e;
int E=GRAPHedges(a,G);
for(UFinit(G->V);E!=0;E=N)
{
for(k=0;k<G->V;k++)
nn[k]=Edge(G->V,G->V,maxWT);
for(h=0,N=0;h<E;h++)
{
i=find(a[h].v);
j=find(a[h].w);
if(i==h)
continue;
if(a[h].wt<nn[i].wt)
nn[i]=a[h];
if(a[h].wt<nn[j].wt)
nn[j]=a[h];
a[N++]=a[h];
}
for(k=0;k<G->V;k++)
{
e=nn[k];v=e.v;w=e.w;
if(v!=G->V&&!UFfind(v,w))
UFunion(v,w);mst[k]=e;
}
}
应用
公路村村通
现有村落间道路的统计数据表中,列出了有可能建设成标准公路的若干条道路的成本,求使每个村落都有公路连通所需要的最低成本。
#include <iostream>
using namespace std;
typedef struct //图的定义
{
int** edges;//邻接矩阵
int n, e; //顶点数,弧数
} MGraph; //图的邻接矩阵表示类型
int cnt = 1;
int Prim(MGraph *G, int v);
int main()
{
MGraph* G;
int N, M, a, b, c;
int i, j;
int money;
cin >> N >> M;
if((N-1)>M)
{
cout<<"-1";
return 0;
}
G = new MGraph;
G->edges = new int* [N + 1];
for (i = 0; i <= N; i++)
G->edges[i] = new int[N + 1];
G->n = N;
G->e = M;
for (i = 1; i <= N; i++)
{
for (j = 1; j <= N; j++)
{
if (i == j)
G->edges[i][j] = 0;
else
G->edges[i][j] = 32767;
}
}
while (M--)
{
cin >> a >> b >> c;
G->edges[a][b] = G->edges[b][a] = c;
}
money = Prim(G, 1);
if (cnt == N)
{
cout << money;
}
else
cout << "-1";
return 0;
}
int Prim(MGraph *G, int v)
{
int min = 32767, lowcost[1001], closest[1001], i, j, index;
int sum = 0, flag = 0;
for (i = 1; i <= G->n; i++)
{
lowcost[i] = G->edges[v][i];
closest[i] = v;
}
for (i = 1; i < G->n; i++)
{
min = 32767;
flag = 0;
for (j = 1; j <= G->n; j++)
{
if (lowcost[j] != 0 && lowcost[j] < min)
{
min = lowcost[j];
index = j;
flag = 1;
}
}
if (flag == 1)
{
sum += min;
cnt++;
}
lowcost[index] = 0;
for (j = 1; j <= G->n; j++)
{
if (lowcost[j] != 0 && G->edges[index][j] < lowcost[j])
{
lowcost[j] = G->edges[index][j];
closest[j] = index;
}
}
}
return sum;
}
打井
农民John 决定将水引入到他的n(1<=n<=300)个牧场。他准备通过挖若干井,并在各块田中修筑水道来连通各块田地以供水。在第i 号田中挖一口井需要花费W_i(1<=W_i<=100,000)元。连接i 号田与j 号田需要P_ij (1 <= P_ij <= 100,000 , P_ji=P_ij)元。请求出农民John 需要为连通整个牧场的每一块田地所需要的钱数。
#include<iostream>
using namespace std;
int g[310][310];
int dist[310];
bool vis[310];
int prime(int n)
{
memset(vis,0,sizeof(vis));
int ans = 0;
for(int i=0;i<=n;i++)
{
dist[i] = g[0][i];
vis[i] = 0;
}
vis[0] = 1;
for(int i=0;i<n;i++)
{
int k = -1,Min = 999999;
for(int j=0;j<=n;j++)
if(!vis[j] && Min > dist[j])
{
k = j;
Min = dist[j];
}
vis[k] = 1;
ans += Min;
for(int j=0;j<=n;j++)
if(!vis[j]&&dist[j] > g[k][j])
dist[j] = g[k][j];
}
return ans;
}
int main()
{
int n;
scanf("%d",&n);
for(int i=0;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&g[i][j]);
for(int i=1;i<=n;i++)
g[i][0] = g[0][i];
printf("%d\n",prime(n));
return 0;
}
最大间隔聚类
给定集合U = {p1, p2, …, pn},对于每对个体pi和pj,d(pi, pj)表示两个个体之间的距离,规定d(pi, pi)=0,d(pi, pj) > 0(i != j),并且d(pi, pj) = d(pj, pi)。
给定参数k(k <= n),将U中的个体划分称为k组,则一个U的k聚类是把U分成k个非空集合C1, C2, …, Ck的划分。我们希望每个聚类内部的点都尽可能地聚集,密集程度尽可能高
而位于两个不同聚类中的点尽可能地相互远离,寻找具有最大可能间隔的k聚类。
我们定义一个k聚类的间隔是处在两个不同聚类中的任何一对点之间的距离的最小值,简单点说就是k个聚类里面任意两个聚类之间的距离的最小值,我们希望这个最小值是所有可能的划分中最大的,
这样,k个聚类就能最大程度地远离彼此。
#include <iostream>
#include <algorithm>
using namespace std;
const int MAX_VERTEX_NUM = 10;
struct Edge {
Edge(int vertex1 = 0, int vertex2 = 0, int weight = 0) {
this->vertex1 = vertex1;
this->vertex2 = vertex2;
this->weight = weight;
}
int vertex1, vertex2, weight;
};
bool operator<(const Edge& e1, const Edge& e2) {
return e1.weight < e2.weight;
}
class MergeQuery {
public:
MergeQuery(const int& vertexNum): vertexNum(vertexNum) {
component = new int[vertexNum];
for (int i = 0; i < vertexNum; ++i) {
component[i] = i;
}
}
~MergeQuery() {
if (component != NULL)
delete [] component;
}
int query(const int& vertex) const { return component[vertex]; }
void merge(int A, int B) {
for (int i = 0; i < vertexNum; ++i) {
if (component[i] == B)
component[i] = A;
}
}
private:
int vertexNum;
int* component;
};
class Kruskal {
public:
Kruskal(const int& vertexNum, const int& edgeNum, const int& KCluster) {
this->vertexNum = vertexNum;
this->edgeNum = edgeNum;
this->KCluster = KCluster;
mq = new MergeQuery(vertexNum);
edges = new Edge[edgeNum];
minimalSpanningTree = new int[vertexNum-KCluster];
}
~Kruskal() {
if (mq != NULL)
delete mq;
if (edges != NULL)
delete [] edges;
}
void getEdge() {
for (int i = 0; i < edgeNum; ++i) {
cin >> edges[i].vertex1 >> edges[i].vertex2 >> edges[i].weight;
}
}
void minimalSpanning() {
sort(edges, edges + edgeNum);
int treeEdgeNum = 0;
for (int i = 0; i < edgeNum && treeEdgeNum < vertexNum-KCluster; ++i) {
int A = mq->query(edges[i].vertex1);
int B = mq->query(edges[i].vertex2);
if (A != B) {
mq->merge(A, B);
minimalSpanningTree[treeEdgeNum++] = i;
}
}
}
void getTree() {
int weightSum = 0;
cout << "K聚类-结果图: (v1, v2, weight)" << endl;
for (int i = 0; i < vertexNum-KCluster; ++i) {
cout << edges[minimalSpanningTree[i]].vertex1 << ' '
<< edges[minimalSpanningTree[i]].vertex2 << ' '
<< edges[minimalSpanningTree[i]].weight << endl;
}
}
private:
int vertexNum;
int edgeNum;
int KCluster;
int* minimalSpanningTree;
MergeQuery* mq;
Edge* edges;
};
int main() {
int vertexNum, edgeNum, KCluster;
cin >> vertexNum >> edgeNum >> KCluster;
if (vertexNum > MAX_VERTEX_NUM) {
cout << "结点数量过多" << endl;
return -1;
}
if (KCluster > vertexNum) {
cout << "聚类数量过大,超过结点数量" << endl;
return -1;
}
Kruskal k(vertexNum, edgeNum, KCluster);
k.getEdge(); // 输入边
k.minimalSpanning(); // kruskal最小生成树算法
k.getTree(); // 输出结果
return 0;
}
最短路径相关算法(Dijkstra(迪杰斯特拉)算法、Floyd(弗洛伊德)算法、SPFA算法)及应用
给定一个有向带权图G=(V,E),顶点s到V中顶点t的最短路径为在E中边的集合S中连接s到t代价最小的路径。当找到S时,我们就解决了单对顶点最短路径问题。要做到这一点,实际上首先要解决更为一般的单源最短路径问题,单源最短路径问题是解决单对顶点最短路径过程中的一部分。在单源最短路径问题中,计算从一个顶点s到其他与之相邻顶点之间的最短路径。之所以要用这个方法解决此问题是因为没有其他更好的办法能用来解决单对顶点最短路径问题。
相关算法
| Dijkstra(迪杰斯特拉)算法 |
算法思想是按路径长度递增的次序一步一步并入来求取,是贪心算法的一个应用,用来解决单源点到其余顶点的最短路径问题。
算法过程:
1.初始化。V为G中所有顶点集合,S={v}。D[x]表示从源点到x的已知路径,初始D[v]为0,其余为无穷大。
2.从源点v开始运行一步广度优先算法即找其相邻点。
3.计算可见点到源点v的路径长度,更新D[x]。然后对路径进行排序,选择最短的一条作为确定找到的最短路径,将其终点加入到S中。
4.从S中选择新加入的点运行广度优先算法找其相邻点,重复step3。直至所有点已加入S或者再搜索不到新的可见点(图中存在不联通的点,此时S<V)终止算法。
typedef struct {
VertexType vexs[MAX_VERtEX_NUM]; //存储图中顶点数据
VRType arcs[MAX_VERtEX_NUM][MAX_VERtEX_NUM]; //二维数组,记录顶点之间的关系
int vexnum,arcnum; //记录图的顶点数和弧(边)数
}MGraph;
typedef int PathMatrix[MAX_VERtEX_NUM]; //用于存储最短路径中经过的顶点的下标
typedef int ShortPathTable[MAX_VERtEX_NUM]; //用于存储各个最短路径的权值和
//迪杰斯特拉算法,v0表示有向网中起始点所在数组中的下标
void ShortestPath_Dijkstra(MGraph G,int v0,PathMatrix *p,ShortPathTable *D){
int final[MAX_VERtEX_NUM];//用于存储各顶点是否已经确定最短路径的数组
//对各数组进行初始化
for (int v=0; v<G.vexnum; v++) {
final[v]=0;
(*D)[v]=G.arcs[v0][v];
(*p)[v]=0;
}
//由于以v0位下标的顶点为起始点,所以不用再判断
(*D)[v0]=0;
final[v0]=1;
int k = 0;
for (int i=0; i<G.vexnum; i++) {
int min=INFINITY;
//选择到各顶点权值最小的顶点,即为本次能确定最短路径的顶点
for (int w=0; w<G.vexnum; w++) {
if (!final[w]) {
if ((*D)[w]<min) {
k=w;
min=(*D)[w];
}
}
}
//设置该顶点的标志位为1,避免下次重复判断
final[k]=1;
//对v0到各顶点的权值进行更新
for (int w=0; w<G.vexnum; w++) {
if (!final[w]&&(min+G.arcs[k][w]<(*D)[w])) {
(*D)[w]=min+G.arcs[k][w];
(*p)[w]=k;//记录各个最短路径上存在的顶点
}
}
}
}
| Floyd(弗洛伊德)算法 |
Floyd算法是一个经典的动态规划算法。是解决任意两点间的最短路径(称为多源最短路径问题)的一种算法,可以正确处理有向图或负权的最短路径问题。(动态规划算法是通过拆分问题规模,并定义问题状态与状态的关系,使得问题能够以递推(分治)的方式去解决,最终合并各个拆分的小问题的解为整个问题的解。)。时间复杂度O(n3),空间复杂度O(n2)
算法过程:
1.首先构建邻接矩阵edge[n+1][n+1],假如现在只允许经过1号节点,求任意两点间的最短距离
2.接下来继续求在只允许经过1和2号两个顶点的情况下任意两点之间的最短距离,在已经实现了从i号顶点到j号顶点只经过前1号点的最短路程的前提下,现在插入第2号节点,来看看能不能更新最短路径,因此只需在步骤一求得的基础上,进行edge[i][j]=min(edge[i][j],edge[i][2]+edge[2][j]);.......
3.需要n次这样的更新,表示依次插入了1号2号.......n号节点,最后求得的edge[i][j]是从i号顶点到j号顶点只经过前n号点的最短路程
typedef struct
{
char vertex[NUMS];
int edges[NUMS][NUMS];
int n,e;
}Graph;
void Floyd(Graph G)
{
int A[NUMS][NUMS],path[NUMS][NUMS];
int i,j,k;
for (i=0;i<G.n;i++)
{
for (j=0;j<G.n;j++)
{
A[i][j]=G.edges[i][j];
path[i][j]=-1;
}
}
for (k=0;k<G.n;k++)
{
for (i=0;i<G.n;i++)
{
for (j=0;j<G.n;j++)
{
if (A[i][j]>A[i][k]+A[k][j])
{
A[i][j]=A[i][k]+A[k][j];
path[i][j]=k;
}
}
}
}
Dispath(A,path,G.n);
}
| Bellman-Ford算法 |
算法思想:给定图G(V, E)(其中V、E分别为图G的顶点集与边集),源点s,数组Distant[i]记录从源点s到顶点i的路径长度,初始化数组Distant[n]为, Distant[s]为0;对于每一条边e(u, v),如果Distant[u] + w(u, v) < Distant[v],则另Distant[v] = Distant[u]+w(u, v)。w(u, v)为边e(u,v)的权值;若上述操作没有对Distant进行更新,说明最短路径已经查找完毕,或者部分点不可达,跳出循环。否则执行下次循环;为了检测图中是否存在负环路,即权值之和小于0的环路。对于每一条边e(u, v),如果存在Distant[u] + w(u, v) < Distant[v]的边,则图中存在负环路,即是说改图无法求出单源最短路径。否则数组Distant[n]中记录的就是源点s到各顶点的最短路径长度。Bellman-Ford算法寻找单源最短路径的时间复杂度为O(V*E).
算法过程:
1.初始化所有点。每一个点保存一个值,表示从原点到达这个点的距离,将原点的值设为0,其它的点的值设为无穷大(表示不可达)。
2.进行循环,循环下标为从1到n-1(n等于图中点的个数)。在循环内部,遍历所有的边,进行松弛计算。
3.遍历途中所有的边(edge(u,v)),判断是否存在这样情况:d(v) > d (u) + w(u,v),则返回false,表示途中存在从源点可达的权为负的回路。
typedef struct Edge //边
{
int u, v;
int cost;
}Edge;
Edge edge[N];
int dis[N], pre[N];
bool Bellman_Ford()
{
for(int i = 1; i <= nodenum; ++i) //初始化
dis[i] = (i == original ? 0 : MAX);
for(int i = 1; i <= nodenum - 1; ++i)
for(int j = 1; j <= edgenum; ++j)
if(dis[edge[j].v] > dis[edge[j].u] + edge[j].cost) //松弛(顺序一定不能反~)
{
dis[edge[j].v] = dis[edge[j].u] + edge[j].cost;
pre[edge[j].v] = edge[j].u;
}
bool flag = 1; //判断是否含有负权回路
for(int i = 1; i <= edgenum; ++i)
if(dis[edge[i].v] > dis[edge[i].u] + edge[i].cost)
{
flag = 0;
break;
}
return flag;
}
| SPFA算法 |
SPFA算法是Bellman-Ford的队列优化,时效性相对好,时间复杂度O(kE)。
实现方法:建立一个队列,初始时队列里只有起始点s,在建立一个数组记录起始点s到所有点的最短路径(初始值都要赋为极大值,该点到他本身的路径赋为0)。然后执行松弛操作,用队列里的点去刷新起始点s到所有点的距离的距离,如果刷新成功且刷新的点不在队列中,则把该点加入到队列,重复执行直到队列为空。
struct egde
{
int to,val,next;
}e[200100];
void spfa()
{
queue<int>q;
q.push(1);
vis[1]=1;
while(!q.empty())
{
int t=q.front();
q.pop();
vis[t]=0;
for(int i=head[t];i!=-1;i=e[i].next)
{
int s=e[i].to;
if(dis[s]>dis[t]+e[i].val)
{
dis[s]=dis[t]+e[i].val;
if(vis[s]==0)
{
q.push(s);
vis[s]=1;
}
}
}
}
}
应用
寻找最短的从商场到赛场的路线。其中商店在1号节点处,赛场在n号节点处,1~n节点中有m条线路双向连接。
先输入n,m,在输入m个三元组,n为路口数,m表示有几条路,其中1为商店,n为赛场,三元组分别表示起点终点,和该路径长,输出1到n的最短距离
#include<iostream>
using namespace std;
#define inf 999999999
#define nmax 110
int n,m,edge[nmax][nmax];
int main ()
{
int a,b;
while(cin>>n>>m&&n!=0)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
edge[i][j]=inf;
}
edge[i][i]=0;
}
while(m--)
{
cin>>a>>b;
cin>>edge[a][b];
edge[b][a]=edge[a][b];
}
for(int k=1;k<=n;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
if(edge[k][j]<inf&&edge[i][k]<inf&&edge[i][j]>edge[i][k]+edge[k][j])
edge[i][j]=edge[i][k]+edge[k][j];
}
}
cout<<edge[1][n]<<endl;
}
}
旅游规划
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
#include<iostream>
#define MAX 500
using namespace std;
typedef struct
{
int len = 0;
int fee = 0;
}node;
node ed[MAX][MAX];
void Dijkstra( int n, int e, int s, int d);
int main()
{
int n, e, s, d, x, y, lenth, fee;
int i, j;
cin >> n >> e >> s >> d;
for (i = 0; i < n; i++)
{
for (j = 0; j < n; j++)
{
ed[i][j].len = ed[j][i].len = 32767;
ed[i][j].fee = ed[j][i].fee = 32767;
}
}
while (e--)
{
cin >> x >> y >> lenth >> fee;
ed[x][y].len = ed[y][x].len = lenth;
ed[x][y].fee = ed[y][x].fee = fee;
}
Dijkstra(n, e, s, d);
return 0;
}
void Dijkstra( int n, int e, int s, int d)
{
int visited[MAX] = { 0 };
node dist[MAX];
int i, j;
int minlen, index;
for (i = 0; i < n; i++)
{
dist[i].len = ed[s][i].len;
dist[i].fee = ed[s][i].fee;
}
visited[s] = 1;
for (i = 0; i < n; i++)
{
minlen = 32767;
for (j = 0; j < n; j++)
{
if (visited[j] == 0 && dist[j].len < minlen)
{
minlen = dist[j].len;
index = j;
}
}
visited[index] = 1;
for (j = 0; j < n; j++)
{
if (visited[j] == 0)
{
if (dist[index].len + ed[index][j].len < dist[j].len)
{
dist[j].len = dist[index].len + ed[index][j].len;
dist[j].fee = dist[index].fee + ed[index][j].fee;
}
else if (dist[index].len + ed[index][j].len == dist[j].len && dist[index].fee + ed[index][j].fee < dist[j].fee)
dist[j].fee = dist[index].fee + ed[index][j].fee;
}
}
}
cout << dist[d].len << " " << dist[d].fee;
}
对图中含有负权的有向图,输出从1号节点到各节点的最短距离,并判断有无负权回路。
#include<iostream>
using namespace std;
#define nmax 1001
#define inf 999999999
int n,m,s[nmax],e[nmax],w[nmax],dst[nmax];
int main ()
{
while(cin>>n>>m&&n!=0&&m!=0)
{
for(int i=1;i<=m;i++)
cin>>s[i]>>e[i]>>w[i];
for(int i=1;i<=n;i++)
dst[i]=inf;
dst[1]=0;
for(int i=1;i<=n-1;i++)
for(int j=1;j<=m;j++)
if(dst[e[j]]>dst[s[j]]+w[j])
dst[e[j]]=dst[s[j]]+w[j];
int flag=0;
for(int i=1;i<=m;i++)
if(dst[e[i]]>dst[s[i]]+w[i])
flag=1;
}
if(flag==1)
cout<<"此图有负权回路"<<endl;
else
{
for(int i=1;i<=n;i++)
{
if(i==1)
cout<<dst[i];
else
cout<<' '<<dst[i];
}
cout<<endl;
}
}
穿城问题
在沙漠中有N个城邦国家(编号0~N-1),每天都有商队从本国出发将本国商品运到其它各个国家,到达各个目的国家后又将该国的商品运回本国。在前往目的国家的路程中,商队可能要需要从其它国家境内穿过。每穿过一个国家商队就需要获得一张该国的通关卡,以便该商队当天沿原路返回时使用。经过多年的摸索,每支商队都已经掌握了国家间的最佳线路(距离最短的路径,不计算在国家内穿过的距离)。
#include<iostream>
#include<algorithm>
using namespace std;
struct Graph{
int V;
int *w;
};
struct Output{
int country;
int card_num;
};
void initGraph(Graph &G,int N){
G.V=N;
G.w=new int[N*N];
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
G.w[i*N+j]=1000;
}
void insert(Graph &G,int start,int end,int w,int *&path_num){
if(G.w[start*G.V+end]==1000){
G.w[start*G.V+end]=G.w[end*G.V+start]=w;
path_num[start*G.V+end]=path_num[end*G.V+start]=1;
}
}
void Floyd(Graph &G,int *&path_num){
for(int s=0;s<G.V;s++){
G.w[s*G.V+s]=0;
}
for(int i=0;i<G.V;i++)
for(int s=0;s<G.V;s++)
for(int e=s+1;e<G.V;e++){
if(G.w[s*G.V+e]>G.w[s*G.V+i]+G.w[i*G.V+e]){
G.w[s*G.V+e]=G.w[e*G.V+s]=G.w[s*G.V+i]+G.w[i*G.V+e];
path_num[s*G.V+e]=path_num[e*G.V+s]=path_num[s*G.V+i]*path_num[i*G.V+e];
}
else if(G.w[s*G.V+e]==G.w[s*G.V+i]+G.w[i*G.V+e]
&& i!=s && i!=e){
path_num[s*G.V+e]+=path_num[s*G.V+i]*path_num[i*G.V+e];
path_num[e*G.V+s]=path_num[s*G.V+e];
}
}
}
void Count(Graph &G,int s,int e,Output *&card,int *&path_num){
for(int i=0;i<G.V;i++){
if(G.w[s*G.V+i]+G.w[i*G.V+e]==G.w[s*G.V+e])
card[i].card_num+=path_num[s*G.V+i]*path_num[i*G.V+e];
}
}
bool cmp(Output x,Output y){
if(x.card_num!=y.card_num)
return x.card_num>y.card_num;
if(x.country!=y.country)
return x.country<y.country;
}
int main(){
int N,E,start,end,w;
cin>>N;
cin>>E;
Graph G;
initGraph(G,N);
int *path_num=new int[N*N]();
for(int i=0;i<E;i++){
cin>>start>>end>>w;
insert(G,start,end,w,path_num);
}
Output *card=new Output[N];
for(int i=0;i<N;i++){
card[i].country=i;
card[i].card_num=0;
}
Floyd(G,path_num);
for(int s=0;s<G.V-1;s++)
for(int e=s+1;e<G.V;e++)
Count(G,s,e,card,path_num);
sort(card,card+N,cmp);
for(int i=0;i<N;i++)
cout<<card[i].country<<" "<<card[i].card_num<<endl;
delete[] card;
delete[] path_num;
delete[] G.w;
return 0;
}
拓扑排序、关键路径以及相关应用
拓扑排序
拓扑排序是将一个AOV网的各个顶点按一定顺序排列,要求满足若存在<Vi,Vj>,则排序中的顶点Vi必在顶点Vj之前。对于同一幅图,拓扑排序可有多个拓扑排序。
算法过程:
(1)从有向图中选择一个无前驱(入度为0)的顶点输出。
(2)删除此顶点,并删除已此顶点为为尾的弧。
(3)重复(1),(2)步骤,知道输出全部顶点或者AOV网中不存在入度为0的顶点。
void TopSort(AdjGraph* G)
{
int i, j, cnt = 0, index = 0;
int number[MAXV]; //用来存放排序之后的元素
int st[MAXV], top = -1;
ArcNode* p;
for (i = 0; i < G->n; i++)
G->adjlist[i].count = 0;
for (i = 0; i < G->n; i++)
{
p = G->adjlist[i].firstarc;
while (p != NULL)
{
G->adjlist[p->adjvex].count++;
p = p->nextarc;
}
}
for (i = 0; i < G->n; i++)
{
if (G->adjlist[i].count == 0)
{
top++;
st[top] = i;
}
}
while (top > -1)
{
cnt++;
i = st[top];
top--;
number[index++] = i;
p = G->adjlist[i].firstarc;
while (p != NULL)
{
j = p->adjvex;
G->adjlist[j].count--;
if (G->adjlist[j].count == 0)
{
top++;
st[top] = j;
}
p = p->nextarc;
}
}
if (cnt != G->n)
cout << "error!";
else
{
for (i = 0; i < index; i++)
{
if (i == 0)
cout << number[0];
else
cout << " " << number[i];
}
}
}
关键路径
在AOE网中,从源点到汇点的所有路径中具有最大路径长度的路径称为关键路径。
算法过程:
(1) 从开始顶点V0出发,假设ve(0)=0,然后按照拓扑有序求出其他各顶点i的最早开始时间ve(i),如果得到拓扑序列中顶点数目小于图中的顶点数,则表示图中存在回路,算法结束,否则继续执行。
(2)从结束顶点Vn出发,假设vl(n-1) = ve(n-1);然后求出各顶点i的最晚发生时间。
(3)根据顶点的最早发生时间,和最晚发生时间,依次求出出每条弧的最早开始时间和最晚开始时间,如果两只相等,则为关键活动。关键活动组成的路径则为关键路径。
void CriticalPath(GraphAdjList GL)
{
EdgeNode *e;
int i,gettop,k,j;
int ete,lte; /*声明活动最早发生时间和最迟发生时间*/
TopoLogicalSort(GL); /*求拓扑序列,计算数组etv和stack2的值*/
ltv = (int*) malloc(GL->numVertexes*sizeof(int)); /*时间的最晚发生时间*/
for(i= 0; i<GL->numVertexes;i++)
ltv[i]=etv[GL->numVertexes-1]; /*初始化ltv[i] 为工程完成的最早时间,etv[i]初始化为0*/
while(top2!=0) /*计算ltv*/
{
gettop = stack2[top2--];
for(e=GL->adjList[gettop].firstedge;e!=NUll;e=e->next)
{/*求各定点事件的最迟发生时间ltv值*/
k=e->adjvex;
if(ltv[k]-e->weight<ltv[gettop])
ltv[gettop]= ltv[k]-e->weight; /*求最晚发生时间,是从拓扑序列的最后一个顶点逆着推导*/
}
}
for(j=0;j<GL->numVertexes;j++) /*求关键活动*/
{
for(e=GL->adjList[j].firstedge;e!=NULL;e=e->next)
{
k=e->adjvex;
ete = etv[j]; /*活动最早开始时间*/
lte = ltv[k] - e->weight;/*活动最晚发生时间*/
if(ete ==lte)
printf("<v%d,v%d> length: %d, ",GL->adjList[j].data,GL->adjList[k].data,e->weight);
}
}
}
应用
剿灭魔教
思路:应用优先队列和拓朴排序结合解题
#include<iostream>
#include<queue>
#include<vector>
#define MAXV 100000
using namespace std;
typedef struct ANode
{
int adjvex; //该边的终点编号
struct ANode* nextarc; //指向下一条边的指针
int info; //该边的相关信息,如权重
} ArcNode; //边表节点类型
typedef int Vertex;
typedef struct Vnode
{
Vertex data; //顶点信息
int count; //入度
ArcNode* firstarc; //指向第一条边
} VNode; //邻接表头节点类型
typedef VNode AdjList[MAXV];
typedef struct
{
AdjList adjlist; //邻接表
int n, e; //图中顶点数n和边数e
} AdjGraph;
void TopSort(AdjGraph* G);
int main()
{
int T, M, N;
AdjGraph *g;
int x, y;
ArcNode* p;
int i;
cin >> T;
while (T--)
{
cin >> M >> N;
g = new AdjGraph;
g->n = M; g->e = N;
for (i = 0; i <= g->n; i++)
g->adjlist[i].firstarc = NULL;
if (N == 0)
{
for (i = 1; i <= M; i++)
cout << i << " ";
cout << endl;
}
else
{
while (N--)
{
cin >> x >> y;
p = new ArcNode;
p->adjvex = x;
p->nextarc = g->adjlist[y].firstarc;
g->adjlist[y].firstarc = p;
}
TopSort(g);
}
}
return 0;
}
void TopSort(AdjGraph* G)
{
int i, j, cnt = 0, index = 0;
int number[MAXV]; //用来存放排序之后的元素
ArcNode* p;
priority_queue<int, vector<int>, greater<int>> q;
for (i = 1; i <= G->n; i++)
G->adjlist[i].count = 0;
for (i = 1; i <= G->n; i++)
{
p = new ArcNode;
p = G->adjlist[i].firstarc;
while (p != NULL)
{
G->adjlist[p->adjvex].count++;
p = p->nextarc;
}
}
for (i = 1; i <= G->n; i++)
{
if (G->adjlist[i].count == 0)
q.push(i);
}
while (!q.empty())
{
p = new ArcNode;
cnt++;
i = q.top();
q.pop();
number[index++] = i;
p = G->adjlist[i].firstarc;
while (p != NULL)
{
j = p->adjvex;
G->adjlist[j].count--;
if (G->adjlist[j].count == 0)
q.push(j);
p = p->nextarc;
}
}
if (cnt != G->n)
cout << "-1 " << endl;
else
{
for (i = 0; i < G->n; i++)
cout << number[i] << " ";
cout << endl;
}
}
AOE网和AOV网
AOE网和AOV网的区别:
一个用顶点表示活动,一个用边表示活动
AOV网侧重表示活动的前后次序,AOE网除了表示活动的前后次序,还表示了活动的持续时间等。
AOV网或AOE网构造拓扑序列的方法:
在有向图中选一个没有前驱(入度为0)的顶点并输出它。
从图中删除该顶点和所有以它为尾的弧。(弧头顶点的入度减一)
重复上述两步,直至全部顶点均已输出。
AOE网
AOE网:在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,边上的权值表示活动的持续时间,称这样的有向图叫做边表示活动的网,简称AOE网。AOE网中没有入边的顶点称为始点(或源点),没有出边的顶点称为终点(或汇点)。AOE网(Activity On Edge Network)是边表示活动的网,AOE网是带权有向无环图。边代表活动,顶点代表 所有指向它的边所代表的活动 均已完成 这一事件。由于整个工程只有一个起点和一个终点,网中只有一个入度为0的点(源点)和一个出度为0的点(汇点)。
AOE网的性质:
⑴ 只有在某顶点所代表的事件发生后,从该顶点出发的各活动才能开始;
⑵ 只有在进入某顶点的各活动都结束,该顶点所代表的事件才能发生。
关键路径:在AOE网中,从始点到终点具有最大路径长度(该路径上的各个活动所持续的时间之和)的路径称为关键路径。
关键活动:关键路径上的活动称为关键活动。关键活动:e[i]=l[i]的活动
由于AOE网中的某些活动能够同时进行,故完成整个工程所必须花费的时间应该为始点到终点的最大路径长度。关键路径长度是整个工程所需的最短工期。
与关键活动有关的量:
(1)事件的最早发生时间ve[k]
ve[k]是指从始点开始到顶点vk的最大路径长度。这个长度决定了所有从顶点vk发出的活动能够开工的最早时间。
(2)事件的最迟发生时间vl[k]
vl[k]是指在不推迟整个工期的前提下,事件vk允许的最晚发生时间。
(3)活动的最早开始时间e[i]
若活动ai是由弧<vk , vj>表示,则活动ai的最早开始时间应等于事件vk的最早发生时间。因此,有:e[i]=ve[k]
(4)活动的最晚开始时间l[i]
活动ai的最晚开始时间是指,在不推迟整个工期的前提下, ai必须开始的最晚时间。若ai由弧<vk,vj>表示,则ai的最晚开始时间要保证事件vj的最迟发生时间不拖后。因此,有:l[i]=vl[j]-len<vk, vj>
AOV网
AOV网(Activity On Vertex NetWork)用顶点表示活动,边表示活动(顶点)发生的先后关系。AOV网的边不设权值,若存在边<a,b>则表示活动a必须发生在活动b之前。若网中所有活动均可以排出先后顺序(任两个活动之间均确定先后顺序),则称网是拓扑有序的,这个顺序称为网上一个全序。
在AOV网上建立全序的过程称为拓扑排序的过程:
(1)在网中选择一个入度为0的顶点输出
(2)在图中删除该顶点及所有以该顶点为尾的边
(3)重复上述过程,直至所有边均被输出。
若图中无入度为0的点未输出,则图中必有环。
#include<stdlib.h>
#include<stdio.h>
#include<string.h>
#define M 10001
int n, m, matrix[M][M], i, j;
int book, indegree[M]; //book 已排序的顶点个数
int main()
{
int a, b, k;
scanf("%d %d",&n, &m);
//init
for (i=1; i<=m; i++) {
scanf("%d %d",&a, &b);
matrix[a][b]=1;
indegree[b]++;
}
for (i=1; i<=n; i++) {
for (j=1; j<=n; j++) {
if (indegree[j] == 0) { //遍历所有入度为0的顶点
indegree[j] = -1;
book++;
for (k=1; k<=n; k++) {
if (matrix[j][k]==1) { //遍历所有入度为1的顶点
matrix[j][k]=0; //remove edge e
indegree[k]--; //update
}
}
break;
}
}
}
printf("%d\n", book);
return 0;
}
动态规划
动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但是一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。动态规划程序设计是对解最优化问题的一种途径、一种方法,而不是一种特殊算法。不像搜索或数值计算那样,具有一个标准的数学表达式和明确清晰的解题方法。动态规划程序设计往往是针对一种最优化问题,由于各种问题的性质不同,确定最优解的条件也互不相同,因而动态规划的设计方法对不同的问题,有各具特色的解题方法,而不存在一种万能的动态规划算法,可以解决各类最优化问题。因此读者在学习时,除了要对基本概念和方法正确理解外,必须具体问题具体分析处理,以丰富的想象力去建立模型,用创造性的技巧去求解。我们也可以通过对若干有代表性的问题的动态规划算法进行分析、讨论,逐渐学会并掌握这一设计方法。
适用条件
1.最优化原理(最优子结构性质) 最优化原理可这样阐述:一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简而言之,一个最优化策略的子策略总是最优的。一个问题满足最优化原理又称其具有最优子结构性质。
2.无后效性将各阶段按照一定的次序排列好之后,对于某个给定的阶段状态,它以前各阶段的状态无法直接影响它未来的决策,而只能通过当前的这个状态。换句话说,每个状态都是过去历史的一个完整总结。这就是无后向性,又称为无后效性。
3.子问题的重叠性 动态规划将原来具有指数级时间复杂度的搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余,这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其它的算法。
大多数动态规划问题都能被归类成两种类型:
- 优化问题:优化问题希望选择一个可行的解决方案,以便最小化或最大化所需函数的值。
- 组合问题:组合问题希望弄清楚做某事方案的数量或某些事件发生的概率。
解决方案的对比:自上而下或者自下而上
自上而下:你从最顶端开始不断地分解问题,直到你看到问题已经分解到最小并已得到解决,之后只用返回保存的答案即可。这叫做记忆存储。
自下而上:你可以直接开始解决较小的子问题,从而获得最好的解决方案。在此过程中,你需要保证在解决问题之前先解决子问题。这可以称为表格填充算法。
算法实现步骤
1、创建一个一维数组或者二维数组,保存每一个子问题的结果,具体创建一维数组还是二维数组看题目而定,基本上如果题目中给出的是一个一维数组进行操作,就可以只创建一个一维数组,如果题目中给出了两个一维数组进行操作或者两种不同类型的变量值,比如背包问题中的不同物体的体积与总体积,找零钱问题中的不同面值零钱与总钱数,这样就需要创建一个二维数组。注:需要创建二维数组的解法,都可以创建一个一维数组运用滚动数组的方式来解决,即一位数组中的值不停的变化,后面会详细徐叙述
2、设置数组边界值,一维数组就是设置第一个数字,二维数组就是设置第一行跟第一列的值,特别的滚动一维数组是要设置整个数组的值,然后根据后面不同的数据加进来变幻成不同的值。
3、找出状态转换方程,也就是说找到每个状态跟他上一个状态的关系,根据状态转化方程写出代码。
4、返回需要的值,一般是数组的最后一个或者二维数组的最右下角。
应用
斐波那契数列
int solutionFibonacci(int n)
{
if(n==0)
return 0;
else if(n == 1)
return 1;
else
{
int result[] = new int[n+1];
result[0] = 0;
result[1] = 1;
for(int i=2;i<=n;i++)
result[i] = result[i-1] + result[i-2];
return result[n];
}
}
数组最大不连续递增子序列
设置一个数组temp,长度为原数组长度,数组第i个位置上的数字代表0...i上最长递增子序列,当增加一个数字时,最大递增子序列可能变成前面最大的递增子序列+1,也可能就是前面最大递增子序列,这需要让新增加进来的数字arr[i]跟前面所有数字比较大小,即当 arr[i] > arr[j],temp[i] = max{temp[j]}+1,其中,j 的取值范围为:0,1...i-1,当 arr[i] < arr[j],temp[i] = max{temp[j]},j 的取值范围为:0,1...i-1,所以在状态转换方程为temp[i]=max{temp[i-1], temp[i-1]+1}
int MaxChildArrayOrder(int a[])
{
int n = a.length;
int temp[] = new int[n];//temp[i]代表0...i上最长递增子序列
for(int i=0;i<n;i++)
temp[i] = 1;
for(int i=1;i<n;i++)
for(int j=0;j<i;j++)
if(a[i]>a[j]&&temp[j]+1>temp[i])
temp[i] = temp[j]+1;
int max = temp[0];
for(int i=1;i<n;i++)
if(temp[i]>max)
max = temp[i];
return max;
}
数组最大连续子序列和
创建一个数组a,长度为原数组长度,不同位置数字a[i]代表0...i上最大连续子序列和,a[0]=arr[0]设置一个最大值max,初始值为数组中的第一个数字。当进来一个新的数字arr[i+1]时,判断到他前面数字子序列和a[i]+arr[i+1]跟arr[i+1]哪个大,前者大就保留前者,后者大就说明前面连续数字加起来都不如后者一个新进来的数字大,前面数字就可以舍弃,从arr[i+1]开始,每次比较完都跟max比较一下,最后的max就是最大值。
int MaxContinueArraySum(int a[])
{
int n = a.length;
int max = a[0];
int sum = a[0];
for(int i=1;i<n;i++)
{
sum = Math.max(sum+a[i], a[i]);
if(sum>=max)
max = sum;
}
return max;
}
数字塔从上到下所有路径中和最大的路径

从上往下看:当从上往下看时,每进来新的一行,新的一行每个元素只能选择他正上方或者左左方的元素,也就是说,第一个元素只能连他上方的元素,最后一个元素只能连他左上方的元素,其他元素可以有两种选择,所以需要选择加起来更大的那一个数字,并把这个位置上的数字改成相应的路径值
开始创建一个一维数组dp[n],初始值只有dp[0]=3,新进来一行时,仍然遵循dp[i][j]=Math.max(dp[i-1][j-1], dp[i-1][j]) + n[i][j],现在为求dp[j],所以现在dp[i-1][j]其实就是数组中这个位置本来的元素即dp[j],而dp[i-1][j-1]其实就是数组中上一个元素dp[j-1],也就是说dp[j]=Math.max(dp[j], dp[j-1])+n[i][j]
int minNumberInRotateArray2(int n[][])
{
int[] temp = new int[n.length];
temp[0] = n[0][0];
for(int i=1;i<n.length;i++)
{
for(int j=i;j>=0;j--)
{
if(j==i)
temp[i]=temp[i-1]+n[i][j];
else if(j==0)
temp[0]+=n[i][0];
else
temp[j]=Math.max(temp[j], temp[j-1])+n[i][j];
}
}
int max = temp[0];
for(int i=1;i<temp.length;i++)
if(temp[i]>max)
max = temp[i];
return max;
}
从下往上看时:从下往上看时大体思路跟从上往下看一样,但是要简单一些,因为不用考虑边界数据,从下往上看时,每进来上面一行,上面一行每个数字有两条路径到达下面一行,所以选一条最大的就可以
具体方法也是建立一个二维数组,最下面一行数据添到二维数组最后一行,从下往上填数字,所以状态转化方程是dp[i][j]=Math.max(dp[i+1][j+1], dp[i+1][j]) + n[i][j],滚动数组,只创建一个一维数组,数组初始值是数字塔最下面一行的值,每次新加一行值,将数组中的值改变,最后数组中第一个数字就是最大路径的值。状态转化方程就是temp[j] = Math.max(temp[j], temp[j+1])+n[i][j]。
int minNumberInRotateArray3(int n[][])
{
int[] temp = new int[n.length];
for(int i=0;i<n.length;i++)
temp[i] = n[n.length-1][i];
for(int i=n.length-2;i>=0;i--)
for(int j=0;j<=i;j++)
temp[j] = Math.max(temp[j], temp[j+1])+n[i][j];
return temp[0];
}
两个字符串最大公共子序列
先创建一个解空间即数组,因为给定的是两个字符串即两个一维数组存储的数据,所以要创建一个二维数组,设字符串X有n个值,字符串Y有m个值,需要创建一个m+1*n+1的二维数组,二维数组每个位置(i,j)代表当长度为i的X子串与长度为j的Y的子串他们的最长公共子串,之所以要多创建一个是为了将边界值填入进去,边界值就是第一行跟第一列,指X长度为0或者Y长度为0时,自然需要填0,其他位置填数字时,当这两个位置数字相同,dp[i][j] = dp[i-1][j-1]+1;当这两个位置数字不相同时,dp[i][j] = Math.max(dp[i][j-1], dp[i-1][j])。最后二维数组最右下角的值就是最大子串。
int MaxTwoArraySameOrderMethod(String str1,String str2)
{
int m = str1.length();
int n = str2.length();
int dp[][] = new int[m+1][n+1];
for(int i=0;i<=m;i++)
dp[i][0] = 0;
for(int i=0;i<=n;i++)
dp[0][i] = 0;
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
if(str1.charAt(i-1) == str2.charAt(j-1))
dp[i][j] = dp[i-1][j-1]+1;
else
dp[i][j] = Math.max(dp[i][j-1], dp[i-1][j]);
}
}
return dp[m][n];
}
背包问题
在N件物品取出若干件放在容量为W的背包里,每件物品的体积为W1,W2……Wn(Wi为整数),与之相对应的价值为P1,P2……Pn(Pi为整数),求背包能够容纳的最大价值。
滚动数组,只创建一个一维数组,长度为从1到W,初始值都是0,能装得下i时,dp[j] = Math.max(dp[j], dp[j-w[i]]+p[i]);装不下时,dp[j] = dp[j];
int PackageHelper2(int n,int w[],int p[],int v)
{
int dp[] = new int[v+1];
for(int i=1;i<=n;i++)
{
for(int j=v;j>0;j--)
{
if(j>w[i])
dp[j] = Math.max(dp[j], dp[j-w[i]]+p[i]);
else
dp[j] = dp[j];
}
}
return dp[v];
}
动态规划和分治区别
动态规划算法:它通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。
分治法:若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果我们能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。我们可以用一个表来记录所有已解的子问题的答案。
1.2.谈谈你对图的认识及学习体会。
- 图可以分为有向图和无向图、还可以分为连通图和非连通图。在图结构中,每个元素可以有零个或多个前驱元素,也可以有零个或多个后继元素,也就是说元素之间的关系是多对多的。图的存储方法有邻接矩阵和邻接表,邻接矩阵顾名思义,是一个矩阵,存储着边的信息的矩阵,而顶点则用矩阵的下标表示,如果是无向图则有A [j ,i] = A[i, j],所以无向图的邻接矩阵是一个对称矩阵;但如果是有向图,则不一定是一个对称矩阵。邻接表可以有效避免内存的浪费,邻接表用一个一维数组存储顶点,利用邻接表建图时候,需要创建多个结构体,如结点类型的结构体,头结点也弄一个结构体,还有邻接表一个结构体。两种不同的存储有各自的优缺点,适用于不同的地方。如果是稀疏图或者需要特定用途的话采用领阶矩阵存储结构的好,反之如果是需要插入删除等操作的话采用邻接表的好。
- 图的两种存储结构:邻接矩阵和邻接表。这两种存储结构都用到了之前学c时学到的结构体,将结构体充分运用。
- 深度遍历算法 : 沿着某一节点一直遍历下去直到没有后继节点,然后回溯,看是否还有节点没有遍历到,重复上述步骤,直到所有节点都被访问过了。如果图不联通,已经访问的节点都回溯完了,仍未找到为访问节点可以用visited[i] 数组查找 。
- 广度遍历算法 : 如同树的层次遍历,一层一层访问节点 ,需要用到队列来储存每层的节点 ,先入队的先对他进行遍历 。
- Prim和Kruscal算法 :最小生成树算法 : Prim算法从任意一个给定的节点开始,每次选择与当前节点集合中权重最小的节点,并将两节点之间的边加入到树中,应用贪心算法 。Kruscal算法 :将每条边的权重按从小到大排列,按照权值的升序来选择边,选择边的同时要注意如果加入该边后形成了回路,就要把这条边删去,选择下一条。
- Dijkstra算法 :最短路径问题 :初始时:先将初始节点与能到的节点之间边的权重记录在dis[]数组内,到不了的记为无穷大 。并用path[]数组记录下一条边的前驱节点作为路径,没有路径记为-1,然后在dis[]数组内选择最小值,则该值就是源点到达该值对应的顶点的最短路径,并把该节点记录到数组T中,在T新加入的节点寻找是否还有更小的边,有则修改dis数组中对应的值,以及path数组的路径 。
- 拓扑排序算法 :在有向图中选一个没有前驱的顶点并且输出,同时将与节点有关的边标记删除。重复操作,若输出的节点数小于原有元素个数,则判定图有环 。
2.阅读代码
2.1 使网格图至少有一条有效路径的最小代价

using PII = pair<int, int>;
class Solution {
private:
static constexpr int dirs[4][2] = { {0, 1}, {0, -1}, {1, 0}, {-1, 0} };
public:
int minCost(vector<vector<int>>& grid) {
int m = grid.size();
int n = grid[0].size();
vector<int> dist(m * n, INT_MAX);
vector<int> seen(m * n, 0);
dist[0] = 0;
deque<int> q;
q.push_back(0);
while (!q.empty()) {
auto cur_pos = q.front();
q.pop_front();
if (seen[cur_pos]) {
continue;
}
seen[cur_pos] = 1;
int x = cur_pos / n;
int y = cur_pos % n;
for (int i = 0; i < 4; ++i) {
int nx = x + dirs[i][0];
int ny = y + dirs[i][1];
int new_pos = nx * n + ny;
int new_dis = dist[cur_pos] + (grid[x][y] != i + 1);
if (nx >= 0 && nx < m && ny >= 0 && ny < n && new_dis < dist[new_pos]) {
dist[new_pos] = new_dis;
if (grid[x][y] == i + 1) {
q.push_front(new_pos);
}
else {
q.push_back(new_pos);
}
}
}
}
return dist[m * n - 1];
}
};
2.1.1 该题的设计思路
一定存在一条最短路径,它只经过每个位置最多一次,这条最短路径只经过了位置 Pk一次。用同样的方法,可以继续删去最短路径中出现超过一次的位置,最终得到一条只经过每个位置最多一次的最短路径。
m == grid.length
n == grid[0].length
将数组 grid建模成一个包含 mn个节点和不超过 4mn条边的有向图 G。图 G 中的每一个节点表示数组 grid中的一个位置,它会向不超过 4个相邻的节点各连出一条边,边的权值要么为 0(移动方向与箭头方向一致),要么为 1(移动方向与箭头方向不一致)
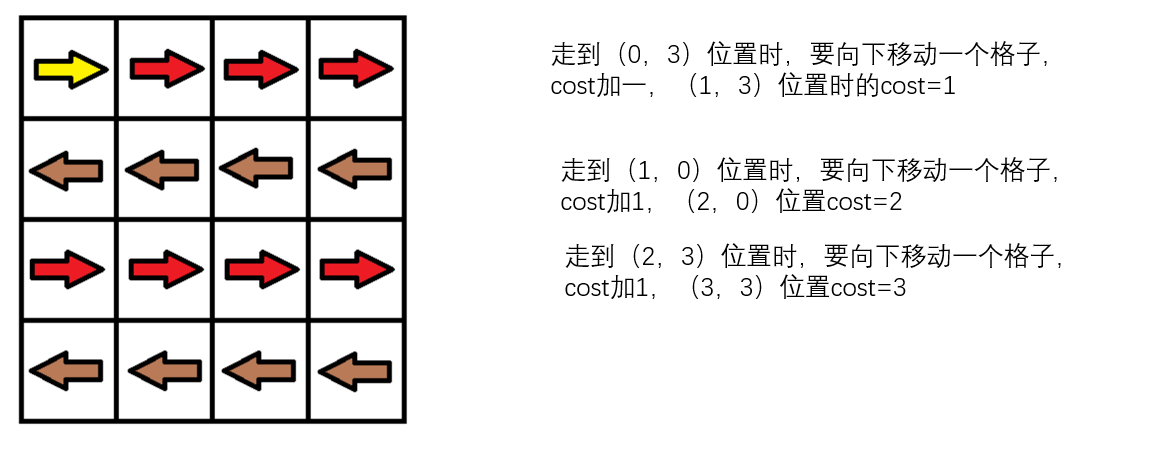
2.1.2 该题的伪代码
定义整型数组 dirs[4][2] = { {0, 1}, {0, -1}, {1, 0}, {-1, 0} };
定义整型变量 m=grid.size();
定义整型变量 n=grid[0].size()
定义双向队列q
定义整型dist[]数组,初值为INF
定义整型seen[]数组,初值为0,判断当前位置是否进行操作过
将0从队头进入
while(队不空)
{
auto cur_pos=q.front()
从队头出队
if(seen[cur_pos]为1)
跳过下列操作
end if
seen[cur_pos]=1
int x = cur_pos / n
int y = cur_pos % n
for int i=0 to 4 do i++
int nx = x + dirs[i][0]
int ny = y + dirs[i][1]
int new_pos = nx * n + ny重新选择新的位置
int new_dis = dist[cur_pos] + (grid[x][y] != i + 1)
if(nx大于或等于0并且小于m,ny大于等于0并且小于n,new_dis小于dist[new_pop]
将dist[new_pos]重新赋值为小的new_dis
if(grid[x][y]等于i+1)
从队头将new_pos入队
else
从队尾将new_pos入队
end if
end if
return dist[m*n-1]
}
2.1.3 运行结果
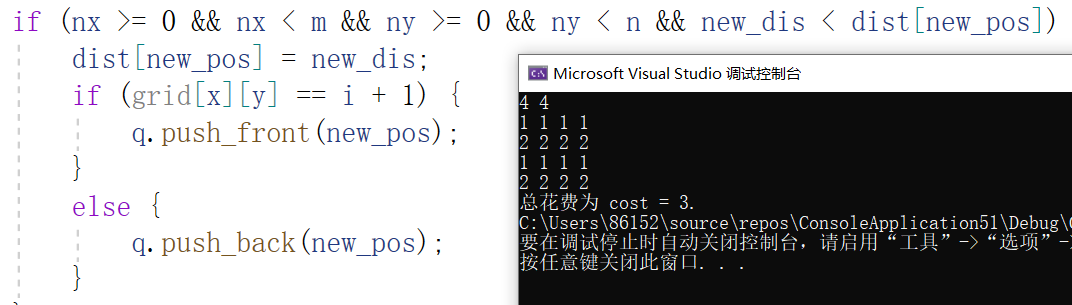
时间复杂度为O(mn)
空间复杂度为O(mn)
2.1.4分析该题目解题优势及难点。
- 优势:按照cost增大的顺序一层一层地bfs,直到找到目的节点。0-1BFS使用了BFS的性质,当前层和下一层的节点的距离最大不超过1,因此当我们碰到w = 0的节点的时候可将其加入队首,如果碰到w = 1的节点的时候将其加入队尾,这样就巧妙的进行了排序工作。任意时刻队列中的节点与源点的距离均为 d 或 d+1(其中 d 为某一非负整数),并且所有与源点距离为 d 的节点都出现在队首附近,所有与源点距离为 d+1 的节点都出现在队尾附近
- 难点:如果边权可能为 0,就会出现如下的情况:源点 s 被取出队列;源点 s 到节点 v1 有一条权值为 1 的边,将节点 v1 加入队列;源点 s 到节点 v2 有一条权值为 0 的边,将节点 v2 加入队列;此时节点 v2 一定会在节点 v1 之后被取出队列,但节点 v2与源点之间的距离反而较小,这样就破坏了广度优先搜索正确性的基础。为了保证广度优先搜索正确性,就要使用双端队列代替普通的队列作为维护节点的数据结构。
2.2 跳跃游戏||
class Solution {
public:
int jump(vector<int>& nums) {
int maxPos = 0, n = nums.size(), end = 0, step = 0;
for (int i = 0; i < n - 1; ++i) {
if (maxPos >= i) {
maxPos = max(maxPos, i + nums[i]);
if (i == end) {
end = maxPos;
++step;
}
}
}
return step;
}
};
2.2.1 该题的设计思路
利用贪心算法进行正向查找,每次找到可到达的最远位置,就可以在线性时间内得到最少的跳跃次数。维护当前能够到达的最大下标位置end,记为边界。我们从左到右遍历数组,到达边界时,更新边界并将跳跃次数增加 1。
初始位置是下标 0,从下标 0 出发,最远可到达下标 2。下标 0 可到达的位置中,下标 1 的值是 3,从下标 1 出发可以达到更远的位置,因此第一步到达下标 1。从下标 1 出发,最远可到达下标 4。下标 1 可到达的位置中,下标 4 的值是 4 ,从下标 4 出发可以达到更远的位置,因此第二步到达下标 4。

2.2.2 该题的伪代码
定义整型变量maxPos=0用来存放选择跳跃的下标的尾指针
定义整型变量n=nums.size()输入数组的大小
定义整型变量end=0作为每一步的跳跃最大下标值
定义整型变量step=0累加跳跃的步数
for int i=0 to n-1 do i++
if(maxPos大于等于i)
将maxPos重置,取maxPos和i+nums[i]中较大的那一个
if(i==end)
end重置为maxPos
step++
end if
end if
return step
2.2.3 运行结果

时间复杂度为O(n)
空间复杂度为O(1)
2.2.4分析该题目解题优势及难点。
- 优势:正向查找可到达的最大位置降低时间复杂度。这道题目的解题思路是贪心算法,可是整个代码运行下来的的时间复杂度并不是很高,贪心算法只要对其进行优化一下,还是可以有效降低时间复杂度的。这道题目将我对贪心算法的看法有了些许的改变,平时都觉得它的代码写下来运行就是要达到平方倍,所以这里就可以看到算法的重要性,老师在上课的时候也一在提醒我们算法优化优化优化!!!
- 难点:利用数组接该题时,如果访问最后一个元素,在边界正好为最后一个位置的情况下,会增加一次「不必要的跳跃次数」,因此不必访问最后一个元素。如果这个地方不注意是很难找出错误的,我当时在代码的时候是很疑惑为什么循环到了n-1就停了,琢磨了挺久才想到边界问题这边。
2.3 冗余连接||

#define NUM 1001
int g_boss[NUM];
int g_inDegree[NUM];
int g_m, g_n;
int FindBoss(int me)
{
if (g_boss[me] != me) {
g_boss[me] = FindBoss(g_boss[me]); // boss's boss
}
return g_boss[me];
}
// true:单连通
bool Valid(int** edges, int dst)
{
for (int i = 1; i <= g_m; i++) { //FindBoss中的参数,有g_m的值,所以,必须有=
g_boss[i] = i;
}
int cnt = 0;
for (int m = 0; m < g_m; m++) {
if (m == dst) {
continue;
}
int mBoss = FindBoss(edges[m][0]);
int nBoss = FindBoss(edges[m][1]);
if (mBoss != nBoss) {
cnt++;
g_boss[nBoss] = mBoss;
}
}
return cnt + 1 == g_m;
}
int* findRedundantDirectedConnection(int** edges, int edgesSize, int* edgesColSize, int* returnSize) {
*returnSize = 0;
g_m = edgesSize;
g_n = *edgesColSize;
memset(g_boss, 0, sizeof(g_boss));
memset(g_inDegree, 0, sizeof(g_inDegree));
for (int i = 0; i < g_m; i++) {
g_inDegree[edges[i][1]]++;
}
int* ret = (int*)malloc(sizeof(int) * 2);
if (ret == NULL) {
return NULL;
}
memset(ret, 0, sizeof(int) * 2);
*returnSize = 2;
for (int m = g_m - 1; m >= 0; m--) {
if (g_inDegree[edges[m][1]] != 2) {
continue;
}
if (Valid(edges, m)) {
ret[0] = edges[m][0];
ret[1] = edges[m][1];
return ret;
}
}
for (int m = g_m - 1; m >= 0; m--) {
if (g_inDegree[edges[m][1]] != 1) {
continue;
}
if (Valid(edges, m)) {
ret[0] = edges[m][0];
ret[1] = edges[m][1];
return ret;
}
}
return ret;
}
2.3.1 该题的设计思路
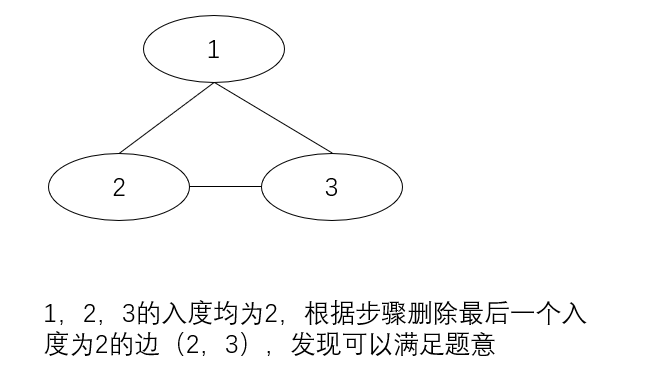
检查是否有入度为2的点, 记录 导致入度为2的 u, v中的 v ;
使用并查集检查所有边, 假设删除最后一个入度为2的边, 第一个边正常处理即可; 遇到形成环的点时, 判定 是否是有入度为2的点的场景, 如果没有, 则当前成环的就是 需要的结果; 如果有入度为2的点, 则当前删除第二组还会导致成环, 说明应该删除的目标是 第一组 u,v;
情况1:是多出的边指向某个非root的结点,该结点记为end,它的入度为2,出度不为0,此时答案只可能为指向end的两条边之一,注意这时候答案唯一,删错边可能导致图不联通,无法构成树。
情况2:与情况1类似,存在入度为2但出度为0的end结点,此时答案不唯一,删掉指向end的哪条边都能使得图变成树,按照题目要求返回最后环内最后出现的边即可
情况:是多出的边指向root,所有结点的入度都是1,此时答案不唯一,删除环内任意边都可以,按照题目要求返回最后环内最后出现的边即可
情况1和2可以合并处理,并查集合并所有边,对于指向end的边只合并第一条,若最后联通分量合并为1,则可以把指向end的第二条边删除,否则只能删除第一条边。
情况3时,用并查集不断合并结点,直到将要合并的顶点已经联通了,则当前边是多余的,可删掉。
2.3.2 该题的伪代码
定义整型数组 g_boss[NUM];
定义整型数组 g_inDegree[NUM];
定义整型变量 g_m, g_n;
//并查集找父亲结点
int FindBoss(int me)
{
if(g_boss[me]不等于me)
递归找到父亲结点g_boss[me]=FindBoss(g_boss[me])
end if
return g_boss[me]
}
//拓扑排序判断是否有环
bool Valid(int** edges, int dst)
{
for int i=1 to g_m do i++
初始化并查集
int cnt=0
for int m=0 to g_m do m++
if(m等于dst)
continue跳过下列语句
end if
int mBoss=FindBoss(edges[m][0])
int nBoss=FindBoss(edges[m][1])
if(mBoss不等于nBoss)
cnt++
将g_boss[nBoss]重置为mBoss
end if
return cnt+1 == g_m
}
int* findRedundantDirectedConnection(int** edges, int edgesSize, int* edgesColSize, int* returnSize)
{
*returnSize = 0;
g_m为二维数组edges的大小
g_n为*edgesColSize
将g_boss、g_inDegree数组置为0
for int i=0 to g_m do i++
g_inDegree[edges[i][1]]++
int* ret = (int*)malloc(sizeof(int) * 2);
if(ret 为空)
return NULL
end if
将ret数组置为0
*returnSize = 2;
for int m=g_m-1 to 0 do m--
if(g_inDegree[edges[m][1]]不等于2)
continue跳过下列语句
end if
if(Valid(edges, m)为1)
ret[0] = edges[m][0]
ret[1] = edges[m][1]
return ret
end if
for int m=g_m-1 to 0 do m--
if(g_inDegree[edges[m][1]]不等于1)
continue跳过下列语句
end if
if(Valid(edges, m)为1)
ret[0] = edges[m][0]
ret[1] = edges[m][1]
return ret
end if
return ret
}
2.3.3 运行结果
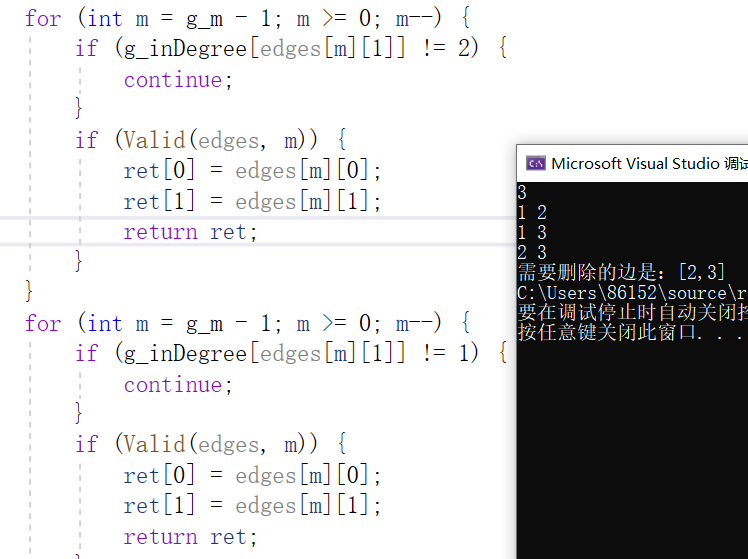
时间复杂度为O(m)
空间复杂度为O(1)
2.3.4分析该题目解题优势及难点。
- 优势:采用并查集和拓扑排序两种算法相结合的思路,很大程度上简化了代码。如果让我去写这个题目,我真的想不到这个解题思路,看这个代码让我学到了很多知识,所以知识点不能局限于课本以及课堂,课外的知识也很重要,学到的知识也要融会贯通。这个题目ret数组用的很巧妙,每一行存放一条边,通过循环观察哪一行才是符合题目要求的输出,这个数组刚开始还没有看懂是什么意思。如果有环,那么答案肯定是删除指向该节点的前一条边;如果没有环,那么答案就是删除的这条边。
- 难点:某个结点可能会有两个父亲结点,结果一定在这个奇葩结点跟它的父亲结点的两条边之中。其二如果先去掉后出现的边再判断剩下的边集是否有环这样可以使代码更简单,如果没有想到这一圈也是很难通过的吧。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号