12 月杂题题解
P4694 Raper
磕 T2 去了,没想到这题部分分是简单费用流。
直接上图,\((S\rightarrow i,1,a_i),(i \rightarrow T',1,b_i)\),不解释。
\((T' \rightarrow T,k,0)\),限流。
\((i\rightarrow i+1,inf,0)\),表示保留到下一天选。
这样就有 56 的高分了。
然后就是模拟费用流了。
直接模拟费用流很难做,其实有更简单的方法。
设 \(f(x)\) 表示生产 \(x\) 张光盘的费用,可以发现这是个凸函数。于是可以用 wqs 二分。
对于这题,显然生产 0 张费用最低。那么让它能生产 \(k\) 张呢?
我们可以二分一个 \(c\),流量每多 \(1\) 就能加上 \(c\),相当于给个奖励。(本题 \(c\leq 0\))。
这样就没有限流的必要了,原图简化为这样:
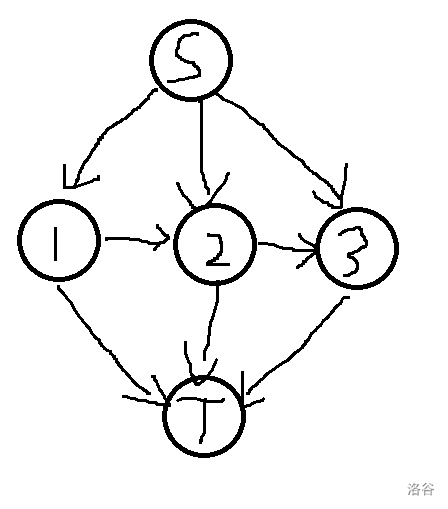
从 \(n\sim 1\) 依次考虑一条路径。
若是一条流向 \(T\) 的路径,那么一定是选一条 \((b_j,1),j\geq i\),其中 \(b_j\) 最小 的边流向 \(T\)。
用一个优先队列维护最小的 \(b_j\),如果这条路径费用 \(\leq 0\),直接流过去,并加入反边(后文解释反边加入什么)。
考虑一条流向 \(S\) 的路径,有两种情况(假设当前考虑点 1)。

这个好办,对于一个 \(i\),如果从 \(S\) 流出去了,那么加入费用为 \(-a_i-c\) 的反边。\(-c\) 因为流量 \(-1\)。
还有一种情况:
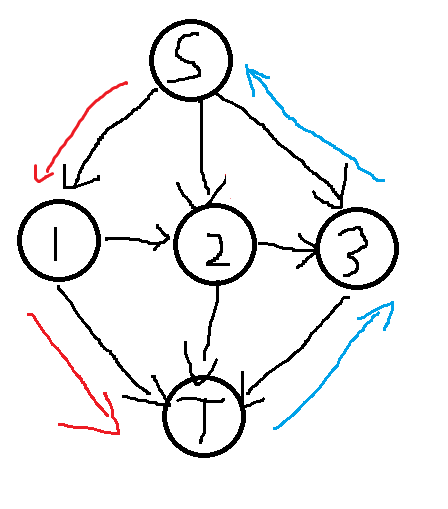
注意蓝色的边显然费用和非负,那么走蓝边对应的正边直接从 \(S\) 流向 \(T\) 费用和为非正,那之前为什么不直接流过去?所以这种情况不存在。
复杂度 \(O(n\log ^2 n)\)
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=5e5+5;
int n,k,ans,cnt,a[N],b[N];
struct node{
int c,w;
bool operator<(const node&x)const{
return c==x.c?w<x.w:c>x.c;
}
};
int f(int c)
{
priority_queue<node> q;
ans=cnt=0;
for(int i=n;i;i--)
{
q.push({b[i],1});
if(a[i]+q.top().c+c<=0)
{
ans+=a[i]+q.top().c+c;
if(q.top().w) cnt++;
q.pop();
q.push({-a[i]-c,0});
}
}
return cnt>=k;
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>k;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
int l=-2e9,r=0,c=0;
while(l<=r)
{
int mid=l+r>>1;
if(f(mid)) c=mid,l=mid+1;
else r=mid-1;
}
f(c);
cout<<ans-k*c<<'\n';
}
A1204 T2 树莓立方体
考虑 k=1 的部分分,就是区间取 min 然后历史版本和。
按行分开维护。
我们维护 \(f(i)\) 表示当前以 \(r\) 为右端点,\(i \sim r\) 的最小值。
可以发现 \(r\) 往后,\(f(i)\) 是单调不增的,也就是 \(r\) 从后往前,\(f(i)\) 是单调上升的。
注意我们有 \(k\) 行,并且要维护 max,我们知道当 \(r\) 往左移一位,某一行某一段值增大了,那么相当于对一段区间取 max。
于是从右往左考虑,维护 \(f(i)\),就是维护删掉 \(r\) 这个值后,会分裂成一些 \(f\) 值相同的区间,二分 + ST 表即可,然后再用吉司机线段树维护区间取 max,历史版本和。
至于分裂的复杂度,你考虑反过来是合并,自然是对的。
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=50005;
int k,n,q,t,A,B,C;
int a[25][N],st[25][16][N],ans[N],ql[N],qr[N];
vector<int> inc[N],cut[N];
int F(int x) {if(!x) return 0;return A^(B*x+C);}
int qmn(int p,int l,int r) {int t=__lg(r-l+1);return min(st[p][t][l],st[p][t][r-(1<<t)+1]);}
struct BIT{
int c1[N],c2[N];
void upd(int x,int v) {for(int V=x*v;x<=n;x+=x&-x) c1[x]+=v,c2[x]+=V;}
int sum(int x) {int s1=0,s2=0;for(int y=x;y;y^=y&-y) s1+=c1[y],s2+=c2[y];return (x+1*s1-s2;}
int qsum(int l,int r) {return sum(r)-sum(l-1);}
}tr1,tr2;
void upd(int l,int r,int v)
{
tr1.upd(l,v),tr1.upd(r+1,-v);
tr2.upd(l,v*t),tr2.upd(r+1,-v*t);
}
struct SegTree{
#define lc (k<<1)
#define rc (k<<1|1)
#define mid (l+r>>1)
int mn[N*4],mx[N*4],tag[N*4];
void pushdown(int k)
{
if(!tag[k]) return;
mn[lc]=mn[rc]=mx[lc]=mx[rc]=tag[lc]=tag[rc]=tag[k];
tag[k]=0;
}
void p_upd(int x,int k=1,int l=1,int r=n)
{
if(l==r) {upd(l,l,-F(mn[k]));mn[k]=mx[k]=0;return;}
pushdown(k);
x<=mid?p_upd(x,lc,l,mid):p_upd(x,rc,mid+1,r);
mn[k]=min(mn[lc],mn[rc]),mx[k]=max(mx[lc],mx[rc]);
}
void t_upd(int x,int y,int v,int k=1,int l=1,int r=n)
{
if(v<=mn[k]) return;
if(l>=x&&r<=y&&mn[k]==mx[k])
{
upd(l,r,F(v)-F(mn[k]));
mn[k]=mx[k]=tag[k]=v;
return;
}
pushdown(k);
if(x<=mid) t_upd(x,y,v,lc,l,mid);
if(mid<y) t_upd(x,y,v,rc,mid+1,r);
mn[k]=min(mn[lc],mn[rc]);
mx[k]=max(mx[lc],mx[rc]);
}
#undef mid
}tr;
inline int rd()
{
int x=0;char c=getchar();
for(;!isdigit(c);c=getchar());
for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^48);
return x;
}
signed main()
{
k=rd(),n=rd(),q=rd();
for(int p=1;p<=k;p++)
{
for(int i=1;i<=n;i++) a[p][i]=st[p][0][i]=rd();
for(int j=1;j<16;j++)
for(int i=1;i+(1<<j)-1<=n;i++)
st[p][j][i]=min(st[p][j-1][i],st[p][j-1][i+(1<<j-1)]);
}
A=rd(),B=rd(),C=rd();
for(int i=1;i<=q;i++)
{
ql[i]=rd(),qr[i]=rd();
inc[ql[i]].push_back(i),cut[qr[i]].push_back(i);
}
for(int i=n;i>=1;i--)
{
t++;
for(int id:cut[i]) ans[id]-=t*tr1.qsum(ql[id],qr[id])-tr2.qsum(ql[id],qr[id]);
if(i+1<=n) tr.p_upd(i+1);
for(int p=1;p<=k;p++)
{
int R=i;
while(R&&a[p][R]>a[p][i+1])
{
int l=1,r=R,L;
while(l<=r)
{
int mid=l+r>>1;
if(qmn(p,mid,R)==a[p][R]) L=mid,r=mid-1;
else l=mid+1;
}
tr.t_upd(L,R,a[p][R]),R=L-1;
}
}
for(int id:inc[i]) ans[id]+=(t+1)*tr1.qsum(ql[id],qr[id])-tr2.qsum(ql[id],qr[id]);
}
for(int i=1;i<=q;i++) cout<<ans[i]<<'\n';
}
A1208 T3 万灵药
赛时 GM_Joanna_ 发明了一种代替 SAM 的假作法,height 树,可惜是假的。但是没人想到 -> 所以没有卡 -> 对的。
考虑 60 pts 的做法。
把所有后缀插入 trie 树,那么就是求一些点两两 lca 深度之和。
考虑插入一个点 \(u\),贡献为到根的树链上所有点点权和,然后把到根的树链上所有点点权 +1,具体可以看此题。
那么可以用树剖维护。由于这题卡常,可以用 BIT 维护区间加区间求和。
现在问题在于我们不能插入所有后缀。
考虑用 SAM。
SAM 建出来是个 DAG,也就是一个结点(状态)可能有多个入边。
我们知道 trie 上的一个结点只会从它的前缀转移过来。
那么在这个 DAG 上,我们也只用保留其前缀转移过来的这条边即可。
观察建 SAM 的过程,可以发现每个点的入边中恰有一条来自它的前缀。所以最后建成了一棵最多 \(2n-1\) 个结点的树。
寻找两个前缀的最长公共后缀,直接在 parent tree 上找 lca 即可。
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e6+5;
ll ans;
char s[N];
int n,q,vis[N],id[N],ch[N][4];
int tot=1,lst=1,PTdn,PTdfn[N],len[N],link[N],st[20][N],dep[N];
int dn,sz[N],fa[N],son[N],dfn[N],top[N];
vector<int> G[N],PT[N];
int ins(int c)
{
int p=lst,q=lst=++tot;len[q]=len[p]+1;
while(p&&!ch[p][c]) ch[p][c]=q,p=link[p];
if(!p) link[q]=1;
else
{
int x=ch[p][c];
if(len[x]==len[p]+1) link[q]=x;
else
{
int y=++tot;len[y]=len[p]+1;
for(int c=0;c<4;c++) ch[y][c]=ch[x][c];
while(p&&ch[p][c]==x) ch[p][c]=y,p=link[p];
link[y]=link[x],link[x]=link[q]=y;
}
}
return q;
}
void PTdfs(int u,int f)
{
dep[u]=dep[f]+1;
PTdfn[u]=++PTdn,st[0][PTdn]=f;
for(int v:PT[u]) PTdfs(v,u);
}
int Min(int u,int v) {return dep[u]<dep[v]?u:v;}
int lca(int u,int v)
{
if(u==v) return u;
u=PTdfn[u],v=PTdfn[v];
if(u>v) swap(u,v);
int t=__lg(v-u++);
return Min(st[t][u],st[t][v-(1<<t)+1]);
}
struct BIT{
int c1[N],c2[N];
void tupd(int x,int v) {for(int V=x*v;x<=dn;x+=x&-x) c1[x]+=v,c2[x]+=V;}
int sum(int x) {int s1=0,s2=0;for(int y=x;y;y^=y&-y) s1+=c1[y],s2+=c2[y];return (x+1)*s1-s2;}
void upd(int l,int r,int v) {tupd(l,v),tupd(r+1,-v);}
int qsum(int l,int r) {return sum(r)-sum(l-1);}
}tr;
void dfs1(int u)
{
sz[u]=1;
for(int v:G[u])
{
fa[v]=u;
dfs1(v);
sz[u]+=sz[v];
if(sz[v]>sz[son[u]]) son[u]=v;
}
}
void dfs2(int u,int topf)
{
top[u]=topf,dfn[u]=++dn;
if(son[u]) dfs2(son[u],topf);
for(int v:G[u]) if(v!=son[u]) dfs2(v,v);
}
void upd(int x,int v)
{
while(top[x]!=1) tr.upd(dfn[top[x]],dfn[x],v),x=fa[top[x]];
if(x!=1) tr.upd(2,dfn[x],v);
}
ll qsum(int x)
{
ll res=0;
while(top[x]!=1) res+=tr.qsum(dfn[top[x]],dfn[x]),x=fa[top[x]];
if(x!=1) res+=tr.qsum(2,dfn[x]);
return res;
}
char buf[1<<15],*p1=buf,*p2=buf;
#define nc() (p1==p2&&(p2=buf+fread(p1=buf,1,1<<15,stdin),p1==p2)?-1:*p1++)
inline int rd()
{
int x=0;char c=nc();
for(;!isdigit(c);c=nc());
for(; isdigit(c);c=nc()) x=(x<<3)+(x<<1)+(c^48);
return x;
}
int main()
{
scanf("%s%d",s+1,&q);
n=strlen(s+1);
for(int i=1;i<=n;i++) id[i]=ins(s[i]-'a');
for(int u=1;u<=tot;u++)
{
PT[link[u]].push_back(u);
for(int i=0,v;i<4;i++) if((v=ch[u][i])&&len[v]==len[u]+1) G[u].push_back(v);
}
PTdfs(1,0);
for(int j=1;j<19;j++)
for(int i=1;i+(1<<j)-1<=PTdn;i++)
st[j][i]=Min(st[j-1][i],st[j-1][i+(1<<j-1)]);
dfs1(1),dfs2(1,1);
while(q--)
{
int x=rd(),y=rd(),u=lca(id[x],id[y]);
if(!vis[u]) vis[u]=1,ans+=qsum(u),upd(u,1);
else vis[u]=0,upd(u,-1),ans-=qsum(u);
cout<<ans<<'\n';
}
}
CF1904E Tree Queries
要放假了,但不想改错,怎么办呢?当然是水博客。
先考虑不删点的一个 \(O(n\log n)\) 做法。
假设当前在点 \(u\),我们维护 \(dis_i\) 表示点 \(u\) 到点 \(i\) 的距离。那么当前的答案就是全局取 max。
考虑往 \(u\) 的儿子 \(v\) 走,那么 \(v\) 子树内的点到 \(v\) 的距离 -2,\(v\) 子树外的点到 \(v\) 的距离 +1。
线段树维护区间加,全局 max。
现在考虑删除一些点,假设当前点为 \(u\),要删的点为 \(x\)。
设 \(T_x\) 表示 \(x\) 的子树。
- 若 \(u\in T_x\),那么我们找到一个点 \(y\in son_x\),且 \(u\in T_y\),保留 \(T_y\)。
- 否则删除 \(T_x\)。
对于删除操作,我们只需要在线段树上打个标记,对于标记的点不要 pushup 即可。
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,m,dn,ans[N],l[N],r[N],id[N],dep[N],f[N][20];
struct node{vector<int> p;int id;};
vector<int> G[N];
vector<node> q[N];
void dfs(int u,int fa)
{
dep[u]=dep[fa]+1,f[u][0]=fa,l[u]=++dn,id[dn]=u;
for(int i=1;i<=18;i++) f[u][i]=f[f[u][i-1]][i-1];
for(int v:G[u]) if(v!=fa) dfs(v,u);
r[u]=dn;
}
#define lc (k<<1)
#define rc (k<<1|1)
#define mid (l+r>>1)
int mx[N*4],add[N*4],lk[N*4];
void pushdown(int k)
{
if(!add[k]) return;
add[lc]+=add[k],add[rc]+=add[k];
mx[lc]+=add[k],mx[rc]+=add[k];
add[k]=0;
}
void pushup(int k)
{
mx[k]=0;
if(!lk[lc]) mx[k]=mx[lc];
if(!lk[rc]) mx[k]=max(mx[k],mx[rc]);
}
void build(int k=1,int l=1,int r=n)
{
if(l==r) {mx[k]=dep[id[l]];return;}
build(lc,l,mid),build(rc,mid+1,r);
mx[k]=max(mx[lc],mx[rc]);
}
void upd(int x,int y,int v,int k=1,int l=1,int r=n)
{
if(l>=x&&r<=y) {mx[k]+=v,add[k]+=v;return;}
pushdown(k);
if(x<=mid) upd(x,y,v,lc,l,mid);
if(mid<y) upd(x,y,v,rc,mid+1,r);
pushup(k);
}
void upd_lk(int x,int y,int v,int k=1,int l=1,int r=n)
{
if(y<x) return;
if(l>=x&&r<=y) {lk[k]=v;return;}
pushdown(k);
if(x<=mid) upd_lk(x,y,v,lc,l,mid);
if(mid<y) upd_lk(x,y,v,rc,mid+1,r);
pushup(k);
}
int find(int x,int rt) {for(int i=18;~i;i--) if(dep[f[x][i]]>dep[rt]) x=f[x][i];return x;}
void dp(int u,int fa)
{
for(auto [v,id]:q[u])
{
for(int x:v)
if(l[x]<=l[u]&&r[u]<=r[x])
{
int p=find(u,x);
upd_lk(1,l[p]-1,1),upd_lk(r[p]+1,n,1);
}
else upd_lk(l[x],r[x],1);
ans[id]=mx[1];
for(int x:v)
if(l[x]<=l[u]&&r[u]<=r[x])
{
int p=find(u,x);
upd_lk(1,l[p]-1,0),upd_lk(r[p]+1,n,0);
}
else upd_lk(l[x],r[x],0);
}
upd(1,n,1);
for(int v:G[u])
{
if(v==fa) continue;
upd(l[v],r[v],-2);
dp(v,u);
upd(l[v],r[v],2);
}
upd(1,n,-1);
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;
for(int i=1;i<n;i++)
{
int u,v;cin>>u>>v;
G[u].push_back(v),G[v].push_back(u);
}
for(int i=1;i<=m;i++)
{
int x,k;cin>>x>>k;
vector<int> v(k);for(int &i:v) cin>>i;
q[x].push_back({v,i});
}
dfs(1,0);
build();
dp(1,0);
for(int i=1;i<=m;i++) cout<<ans[i]-1<<'\n';
}
CF1904F Beautiful Tree
若确定 \(a<b\),我们连一条有向边 \(a\rightarrow b\),最后拓扑即可。
但边数是 \(O(n^2)\),考虑优化建图。
介绍一种树上倍增优化建图的方法。
定义 \(up(u,i)\) 表示 \(u\) 往上跳 \(i\) 次到达的祖先。
对于一个结点 \(u\),新建一个点 \(f1(u,i)\) 表示对于 \(\forall x\in[0,2^{i}-1]\),连边 \(u\rightarrow up(u,x)\)。
显然有连边 \(f1(u,i)\rightarrow f1(u,i-1),f1(u,i)\rightarrow f1(up(u,2^i),i-1)\)。
初始化 \(f1(u,0)\rightarrow u\)。
这样边数就优化到了 \(n\log n\) 级别。
但是注意到在一条路径上,我们不能连自环 \(c\rightarrow c\),在倍增跳的时候注意下实现即可。
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,m,tot,ans[N],d[N*40],pre[N*40];
vector<int> G[N];
struct edge{int to,nxt;} e[N*200];
void add(int u,int v) {if(!u||!v) return;e[++tot]={v,pre[u]};pre[u]=tot;++d[v];}
int cnt,dep[N],f[N][18],f1[N][18],f2[N][18];
void dfs(int u,int fa)
{
dep[u]=dep[fa]+1;
f[u][0]=fa,f1[u][0]=f2[u][0]=u;
for(int i=1,l=__lg(dep[u]);i<=l;i++)
{
f[u][i]=f[f[u][i-1]][i-1];
f1[u][i]=++cnt,add(cnt,f1[u][i-1]),add(cnt,f1[f[u][i-1]][i-1]);
f2[u][i]=++cnt,add(f2[u][i-1],cnt),add(f2[f[u][i-1]][i-1],cnt);
}
for(int v:G[u]) if(v!=fa) dfs(v,u);
}
int lca(int u,int v)
{
if(dep[u]<dep[v]) swap(u,v);
for(int i=17;~i;i--) if(dep[f[u][i]]>=dep[v]) u=f[u][i];
if(u==v) return u;
for(int i=17;~i;i--) if(f[u][i]!=f[v][i]) u=f[u][i],v=f[v][i];
return f[u][0];
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
cin>>n>>m;cnt=n;
for(int i=1;i<n;i++)
{
int u,v;cin>>u>>v;
G[u].push_back(v),G[v].push_back(u);
}
dfs(1,0);
while(m--)
{
int op,u,v,x;cin>>op>>u>>v>>x;
int l=lca(u,v),y=v;
for(int i=17;~i;i--) if(dep[f[y][i]]>=dep[x]) y=f[y][i];
if(y==x) swap(u,v);
if(op==1)
{
for(int i=17;~i;i--) if(dep[f[u][i]]>=dep[x]) add(x,f1[u][i]),u=f[u][i];u=f[x][0];
for(int i=17;~i;i--) if(dep[f[u][i]]>=dep[l]) add(x,f1[u][i]),u=f[u][i];
for(int i=17;~i;i--) if(dep[f[v][i]]>=dep[l]) add(x,f1[v][i]),v=f[v][i];
if(l!=x) add(x,l);
}
if(op==2)
{
for(int i=17;~i;i--) if(dep[f[u][i]]>=dep[x]) add(f2[u][i],x),u=f[u][i];u=f[x][0];
for(int i=17;~i;i--) if(dep[f[u][i]]>=dep[l]) add(f2[u][i],x),u=f[u][i];
for(int i=17;~i;i--) if(dep[f[v][i]]>=dep[l]) add(f2[v][i],x),v=f[v][i];
if(l!=x) add(l,x);
}
}
queue<int> q;int now=0;
for(int i=1;i<=cnt;i++) if(!d[i]) q.push(i);
while(!q.empty())
{
int u=q.front();q.pop();
if(u<=n) ans[u]=++now;
for(int i=pre[u];i;i=e[i].nxt)
{
int v=e[i].to;
if(!--d[v]) q.push(v);
}
}
if(now<n) puts("-1");
else for(int i=1;i<=n;i++) cout<<ans[i]<<' ';
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号