Radio Coverage

Radio Coverage

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 735		Accepted: 218		Special Judge

Description

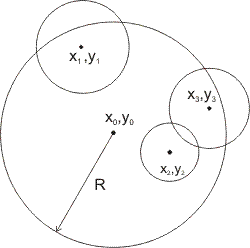Radio station 'ACM Rock' is broadcasting over the circular area with center in point (x0, y0) and radius R. In order to increase the auditorium, it were suggested to build several relay stations. N locations were selected as candidate sites for relay stations. Relay station placed in i-th location will cover a circular area with center in point (xi, yi) and radius ri, where center lies inside the area covered by the base station, (x0 - xi)² + (y0 - yi)²≤ R². 

Your task is to select a subset of sites for relay stations so that: 

1. the covered areas for relays do not intersect (but may touch) one another, 
2. the total area covered by base station and all relays is maximum possible.

Input

Input contains integer number N followed by real numbers x0 y0 R, followed by N triples of real numbers xi yi ri. 
1 ≤ N ≤ 10, 0 ≤ xi, yi, x0, y0 ≤ 1000, 1 ≤ ri ≤ R ≤ 1000.

Output

Output should contain a single real number -- the maximal coverage area with the absolute error less than 10⁻².

Sample Input

1 0 0 10 10 0 10

Sample Output

505.4816

Source

Northeastern Europe 2004, Far-Eastern Subregion

 

题意:求圆心在初始圆内的并且除了初始圆外其他任意两圆两两不相交，内切，内含的面积，使得这个面积最大。

 

不知道为什么GCC总是过不了，用了C就AC了

 

code:

#include <stdio.h>

#include <string.h>

#include <stdlib.h>

#include <math.h>

#define pi acos(-1.)

#define le 12

const double eps = 1e-8;

typedef struct{

    double x,y,r;

}re;

re p[le];

int N,k,vis[le];

double ans;

 

double max(double a,double b){

    return a > b ? a : b;

}

 

int in_circle(re a,re b){

    double x = (a.x - b.x);

    double y = (a.y - b.y);

    double dist = x * x + y * y;

    return (dist < a.r * a.r + eps && sqrt(dist) > a.r - b.r + eps);

}

 

double dis(re a,re b){

    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));

}

 

int intersect(re a,re b){

    return dis(a,b) < a.r + b.r - eps;

}

 

double triangle_area(double r,double r2,double d){

    double h = (r + r2 + d) / 2;

    return sqrt(h * (h - r) * (h - r2) * (h - d));

}

 

double in_area(re a,re b){

    double d = dis(a,b);

    double s = triangle_area(a.r,b.r,d);

    double angle  = acos((a.r * a.r + d * d - b.r * b.r) / (2 * a.r * d));

    double angle2 = acos((b.r * b.r + d * d - a.r * a.r) / (2 * b.r * d));

    return angle * a.r * a.r + angle2 * b.r * b.r - 2 * s;

}

 

double area(re a,re b){

    return pi * b.r * b.r - in_area(a,b);

}

 

void input(){

    int i;

    for(i = 0;i <= N;i++)

        scanf("%lf%lf%lf",&p[i].x,&p[i].y,&p[i].r);

}

 

void available(){

    int i;

    k = 1;

    for(i = 1;i <= N;i++)

        if(in_circle(p[0],p[i]))

            p[k++] = p[i];

}

 

void dfs(int ind,double sum){

    int i;

    for(i = 1;i < k;i++)

        if(vis[i] && intersect(p[ind],p[i]))

            return ;

    vis[ind] = 1;

    sum += area(p[0],p[ind]);

    ans = max(ans,sum);

    for(i = 1;i < k;i++)

        if(!vis[i]) dfs(i,sum);

    vis[ind] = 0;

}

 

void enmue(){

    int i;

    double sum;

    ans = pi * p[0].r * p[0].r;

    for(i = 1;i < k;i++){

        memset(vis,0,sizeof(vis));

        sum = pi * p[0].r * p[0].r;

        dfs(i,sum);

    }

}

 

void deal(){

    available();

    enmue();

    printf("%.4lf\n",ans);

}

 

int main(void){

    while(scanf("%d",&N) == 1){

        input();

        deal();

    }

    return 0;

}