信号复习
第一章信号与系统
作者：莫钟雨
作者（大三学生）水平有限，如有错误，敬请谅解
参考资料：《信号与系统（第二版）》· 奥本海姆
本章思维导图
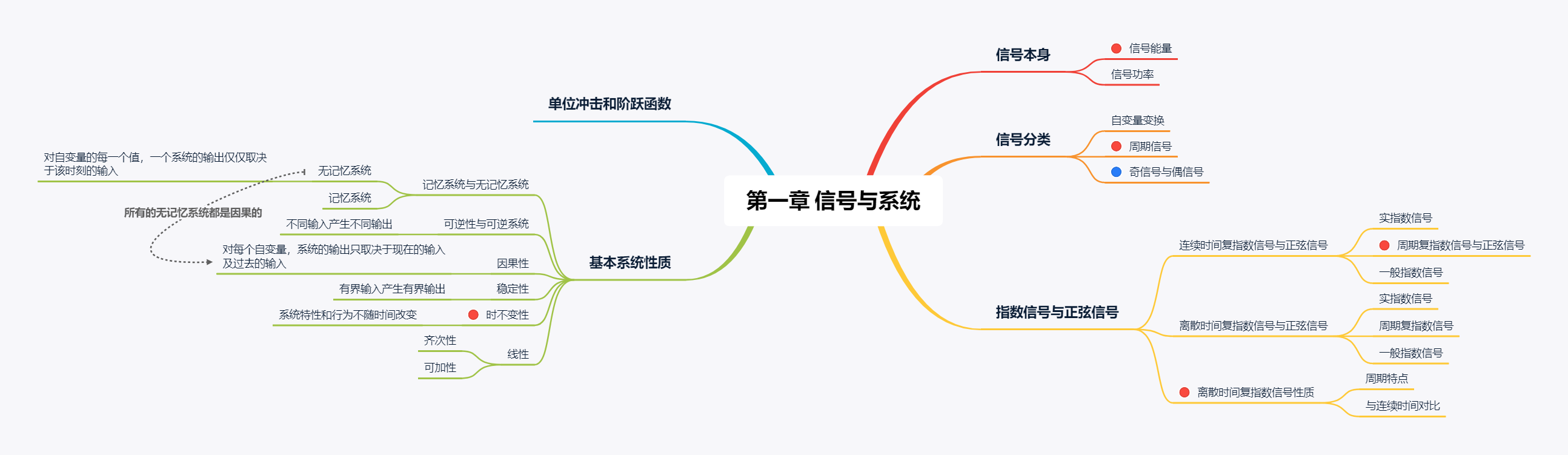
信号本身
信号可以描述范围及其广泛的一类物理现象，但在所有情况下，信号所包含的信息总是寄寓在某种变化形式的波形中。
信号能量
-
连续时间
\[{E_\infty} = \int_{-\infty}^{+\infty} {|x(t)|}^2 dt \] -
离散时间
\[{E_\infty} = \sum_{n=-\infty}^{+\infty} {|x[n]|}^2 \]
信号功率
-
连续时间
\[{P_\infty} \approx\lim^{}_{T \to \infty} \int_{-T}^{+T} {|x(t)|}^2 dt \] -
离散时间
\[{P_\infty} \approx\lim^{}_{N \to \infty} \frac{1}{2N+1}\sum_{n=-N}^{+N} {|x[n]|}^2 \]
信号分类
自变量变换
- 时移
- 时间反转
- 时间尺度变换
周期信号
一个周期连续时间信号，存在一个正值的 \(T\)，对所有 \(t\) 来说，有
\[x(t) = x(t + T)
\]
换句话说，当一个信号\(x(t)\)时移\(T\) 后其值不变，这时就说\(x(t)\)是周期信号
奇信号与偶信号
任何信号都可以分解为一个奇信号和一个偶信号之和。
指数信号与正弦信号
连续时间复指数信号与正弦信号
\[x(t) = Ce^{at}
\]
-
实指数信号(\(C\)和\(a\)都是常数)
图像类似于指数函数
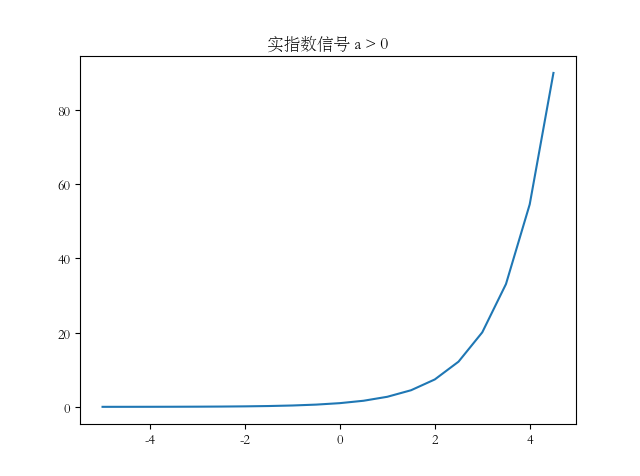
- 周期复指数信号（将\(a\)限制为纯虚数）与正弦信号
当\(a\)为纯虚数时，\(x(t) = e^{jw^{}_{0}t}\)是周期信号，下面是推证：
若存在\(T\)使得，\(e^{jw_0t}=e^{jw_0(t + T)}\)成立,则x(t)是周期的。
\[e^{jw_0(t + T)} = e^{jw_0t}*e^{jw_0T}
\]
在\(e^{jw_0T} = 1\)时，\(x(t)\)是周期的，此时根据欧拉公式（\(e^{j\pi} + 1 = 0\)）可得：
\[T_0 = \frac{2\pi}{|w_0|}
\]
\(T_0\)就是基波周期
- 一般复指数信号（\(C和a\)都是复数）
\[Ce^{at} = |C|e^{j\Theta}e^{(r + jw_0)t} = |C|e^{rt}e^{j(w_0t + \Theta)}
\]
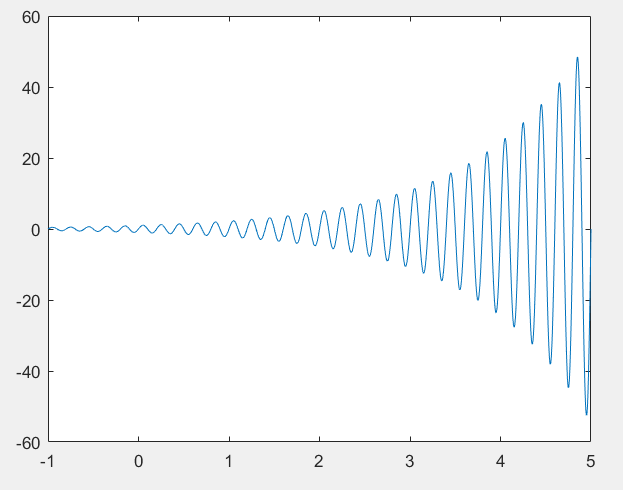
离散时间复指数信号与正弦信号
-
实指数信号
与连续时间基本一致
-
周期复指数信号
重新审视连续时间周期复指数信号周期性成立的条件：
\[e^{jw_0T} = 1 \]等效于连续时间内的：
\[e^{jw_0N} = 1 \]要满足此条件意味着：
\[w_0N = 2\pi m (m为整数) \]即：
\[\frac{w_0}{2\pi} = \frac{m}{N} \]当\(\frac{w_0}{2\pi}\)为有理数时，\(x(t)\)为周期信号
-
一般指数信号
与连续时间基本一致
离散时间复指数信号性质（略）
-
周期特点
-
与连续时间对比
基本系统性质
记忆系统与无记忆系统
-
无记忆系统
- 对自变量的每一个值，一个系统的输出仅仅取决于该时刻的输入
-
记忆系统
可逆性与可逆系统
- 不同输入产生不同输出
因果性
- 对每个自变量，系统的输出只取决于现在的输入及过去的输入
稳定性
- 有界输入产生有界输出
时不变性
- 系统特性和行为不随时间改变
- \(输入x_1(t),响应为y_1(t), 当输入为x_1(t - t_0)时，产生响应y_1(t - t_0)\)
线性
- 齐次性
- \(ay_1(t)是对ax_1(t)的响应,此处a为任意复常数\)
- 可加性
- \(y_1(t) + y_2(t)是对x_1(t) + x_2(t)的响应\)
