解题报告

牛客网NOIP赛前集训营-提高组（第二场）

 

A 方差

题目大意：

一个长度为 m 的序列 b[1...m] ，我们定义它的方差为 ，其中  表示序列的平均值。

可以证明的是，如果序列元素均为整数，那么方差乘以 m^2 之后，得到的值一定是整数。

现在有一个长度为 N 的序列 a[1...N]，对每个 i = 1~N，你需要计算，如果我们删除 a[i]，剩下的 N-1 个元素的方差乘以 (N-1)^2 的值。

 

题解：将式子化简，对于方差，其实只求一个和的平方和平方的和 

化简如下：

 

 

 

 

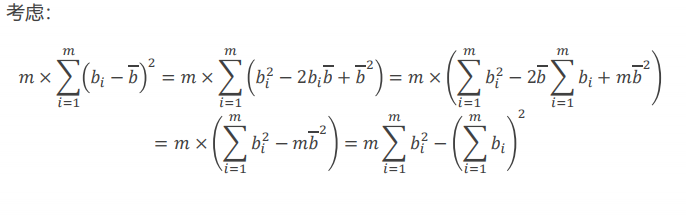
B 分糖果

题目大意：

N 个小朋友围成一圈，你有无穷个糖果，想把其中一些分给他们。
从某个小朋友开始，我们顺时针给他们标号为 1 ~ N。第 i 个小朋友可以得到至多 a[i]，至少 1 个糖果。
问，有多少种分配方案使得每一对相邻的小朋友拿到的糖果数不同。答案对 10^9 + 7 取模。

部分分做法

分糖果 考虑 N 和 a[i] 均不是很大的情形，此时我们可以DP 把环从某个位置断开，记 𝑓 𝑖 𝑗 𝑘 表示考虑了前 i 个人，第 1 个人和第 i 个人分别了 j k 个糖果的方案数 暴力转移的复杂度是 Θ 𝑎𝑖 ，如果加一个简单的前缀和优化的话就能优化到 Θ 1

 

容斥的想法

分糖果 正难则反，我们考虑容斥 枚举哪些相邻的小朋友拿到的糖果数一样，整个环根据我们枚举的相等关系会被分成若干段 其中每段的糖果数一样，那么这一段的方案数必然为这段中的 𝑎𝑖 最小值 同时，假设我们枚举了 𝑘 个相等关系，它的容斥系数为 −1 𝑘 我们考虑 DP 它的贡献，设 𝑓𝑖 表示： 容斥到第 i 个元素，前面划分了若干段，所有不同的方案配上容斥系数的贡献之和

$𝑓𝑖 = \sum_𝑗 𝑓_𝑗 × min (𝑎 [𝑗 + 1 … 𝑖]) × −1 ^{𝑖−𝑗−1}$

 

C 集合划分

题目大意：

visit_world得到了 {1, 2, ... , n} 的 (2^n - 1) 个非空子集 他计划把这些集合分给小 S 和小 T，每个子集恰好给其中一个人。 分配规则是这样的： 1. 若存在两个集合属于同一个人，那么这两个集合的并也要属于那个人 2. 有 m 个集合是小 S 特别喜欢的，你要把这些集合全部给小 S 3. 小 S 拿到了恰好 k 个集合。 请给出一种方案，或者说明无解

 

对于部分分的做法：

M = 0 的做法

我们定义 lowbit(x) 为 x 的二进制下，最小的一个元素（换句话说，就是它对应集合里最小的元素） 我们用 x | y 表示 x 和 y 两个集合的并 断言：我们把所有 lowbit 相同的元素都分给同一个人，这样构造的方案一定是合法的 证明很容易，注意到 lowbit(x | y) 恰好是 lowbit(x) 和 lowbit(y) 之一，若 lowbit(x) 和 lowbit(y) 均属于 A，那么 lowbit(x | y) 也属于 A lowbit(x) = i 的元素恰好有 2^(N-i-1) 个，我们把 K 二进制拆分，构造答案即可

 

M > 0 的做法

把上述做法推广一下，我们给每个元素定义一个优先级，使得不同元素优先级不同 对一个集合，我们定义它的“特征”为它之中优先级最高的元素编号 那么，我们把所有“特征”相同的集合分给同一个人，这样一定合法 另一方面，我们可以证明，每一种合法方案都可以按照这种方法构造 所以我们问题有两个： • 确定每个元素的优先级，从而计算集合的特征 • 把特征相同的集合分给同一个人 一个观察是，第二个问题其实是不需要考虑的，因为有 K 的限制，每个集合分给谁是确定好的

 

使用状压DP，从高到低确定每个元素的优先级 记 𝑓[𝑆] 表示集合 S 里的元素已经被分配了最高的若干优先级，是否可行 转移时枚举接下来的优先级最高的元素是哪个，使用一些简单的位运算技巧确定可行性 最后根据这个 DP 还原出一种方案即可。