一些常见的数据结构总结

1、线性表

1.1、数组

数组是可以再内存中连续存储多个元素的结构，在内存中的分配也是连续的，数组中的元素通过数组下标进行访问，数组下标从0开始。

1.2、链表

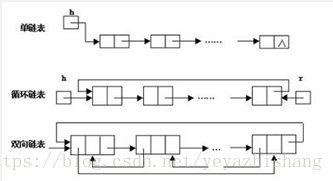
链表是物理存储单元上非连续的、非顺序的存储结构，数据元素的逻辑顺序是通过链表的指针地址实现，每个元素包含两个结点，一个是存储元素的数据域 (内存空间)，另一个是指向下一个结点地址的指针域。根据指针的指向，链表能形成不同的结构，例如单链表，双向链表，循环链表等。

2、散列表

2.1、哈希（Hash）

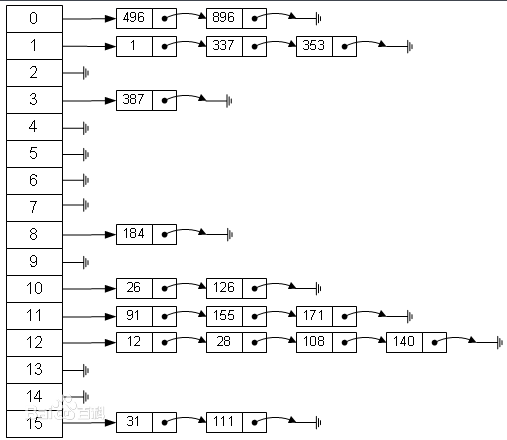
散列表，也叫哈希表，是根据关键码和值 (key和value) 直接进行访问的数据结构，通过key和value来映射到集合中的一个位置。

记录的存储位置=f(key)

这里的对应关系 f 成为散列函数，又称为哈希 (hash函数)，而散列表就是把Key通过一个固定的算法函数既所谓的哈希函数转换成一个整型数字，然后就将该数字对数组长度进行取余，取余结果就当作数组的下标，将value存储在以该数字为下标的数组空间里。

因为哈希表是基于数组衍生的数据结构，在添加删除元素方面是比较慢的，所以很多时候需要用到一种数组链表来做，

有很多问题要考虑，比如哈希冲突的问题，解决方案有开发定址法和链地址法。

2.1.1、链地址法

也叫拉链法。拉链法是数组结合链表的一种结构。如在JDK1.7中HashMap的底层就是这样的。

 

3、栈和队列

3.1、队列

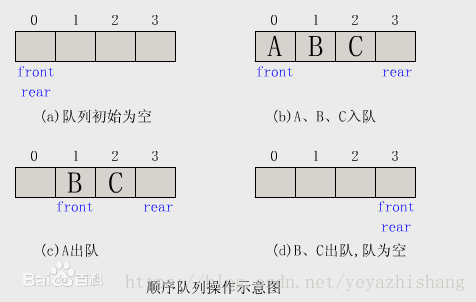
队列可以在一端添加元素，在另一端取出元素，也就是：先进先出。从一端放入元素的操作称为入队，取出元素为出队。

3.2、栈

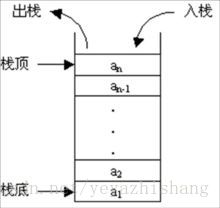
栈的结构就像一个集装箱，越先放进去的东西越晚才能拿出来。先进后出，或者说是后进先出，从栈顶放入元素的操作叫入栈，取出元素叫出栈。

4、树结构

4.1、二叉树

每个节点最多含有两个子树的树称为二叉树。

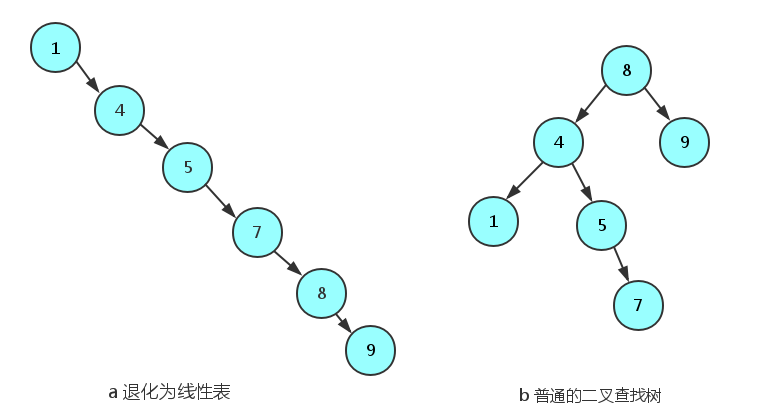
在某些极端的情况下（如在插入的序列是有序的时），二叉查找树将退化成近似链或链。

4.2、平衡二叉树（AVL树）

平衡二叉树是基于二叉查找树的改进。在某些极端情况下，二叉查找树将退化成近似链或链，我们通过自平衡操作（即旋转）构建两个子树高度差不超过1的平衡二叉树。

4.3、红黑树

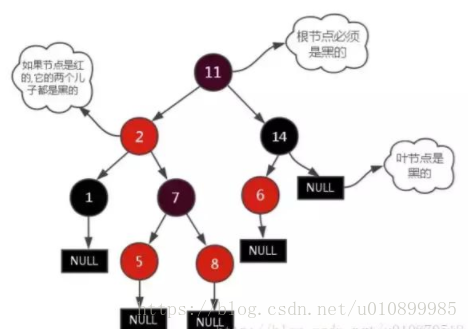
红黑树也是一种自平衡的二叉查找树。红黑树确保没有一条路径会比其他路径长出两倍。

• 每个结点非黑即红。

• 根结点是黑的。

• 每个叶结点（叶结点即指树尾端NIL指针或NULL结点）都是黑的。

• 如果一个结点是红的，那么它的两个儿子都是黑的。(不能有两个连续节点为红色)

• 对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。

4.4、B树

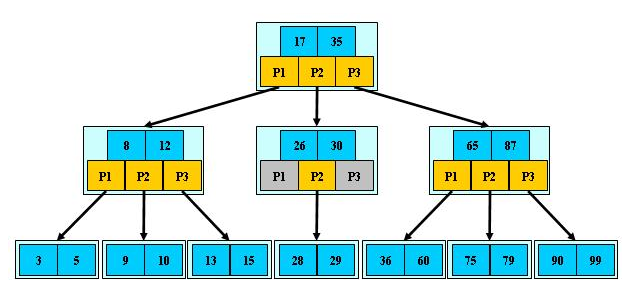
B树（英语：B-tree）是一种自平衡的树，能够保持数据有序。可以认为是m叉的多路平衡查找树。它的每个节点最多包含m个孩子（子节点），m称为b树的阶，m的大小取决于磁盘页的大小。

• 定义任意非叶子结点最多只有M个儿子，且M>2；

• 根结点的儿子数为[2, M]；

• 除根结点以外的非叶子结点的儿子数为[M/2, M]，向上取整；

• 非叶子结点的关键字个数=儿子数-1；

• 所有叶子结点位于同一层；

• k个关键字把节点拆成k+1段，分别指向k+1个儿子，同时满足查找树的大小关系。

如图，是一个（M=3）3阶B树。

4.5、B+树

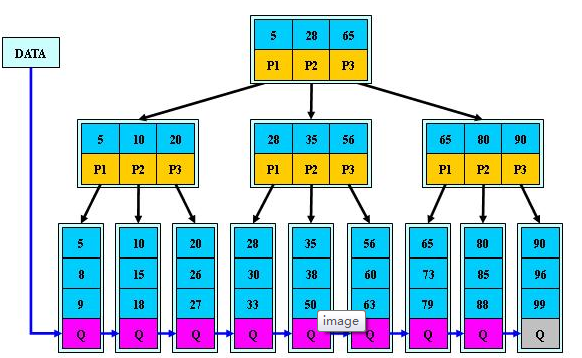
是b树的一种变体，查询性能更好，通常用于关系型数据库（如Mysql）和操作系统的文件系统中。元素自底向上插入，这与二叉树恰好相反。

在B树基础上，为叶子结点增加链表指针（B树+叶子有序链表），所有关键字都在叶子结点中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中。

b+树的非叶子节点不保存数据，只保存子树的临界值（最大或者最小），所以同样大小的节点，b+树相对于b树能够有更多的分支，使得这棵树更加矮胖，查询时做的IO操作次数也更少。

同一个数字会在不同节点中重复出现，根节点的最大元素就是b+树的最大元素。

• 所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好是有序的。

• 不可能在非叶子结点命中。

• 非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层。

• 更适合文件索引系统。原因： 增删文件（节点）时，效率更高，因为B+树的叶子节点包含所有关键字，并以有序的链表结构存储，这样可很好提高增删效率。

如图，是一个（M=3）3阶B+数。