leetcode 322 零钱兑换

 

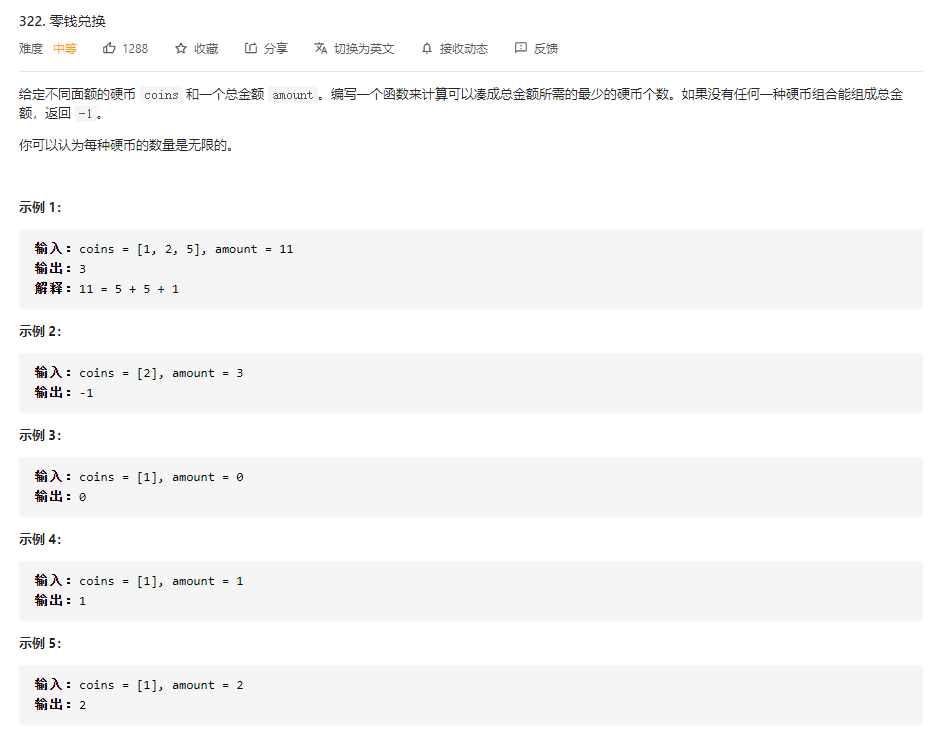
 　　这道题一看题就能猜到肯定是动态规划了，因为你穷举的话：第一个硬币有n种拿法，第二个硬币有n种拿法，这下去量级可就太大了。问题是，动态规划，怎么规划能规划出来，而且比较便于人类理解呢？

　　当然是dp[i]代表总面值为 i 我们需要dp[i]个硬币比较合理。

　　之后我们可以通过dp[i - m] + 1 来推理出dp[i]，这里m是各种面值的硬币，我们只需要填补上最后一块硬币就可以了。

　　在第一个循环中我们目的是计算总金额为1、为2、为3为4一直到为amount个需要最少多少个硬币；在第二个循环中，对应当前计算的金额如果是8，我们要从所有类型的硬币拿出来进行查询，例如我们只有1、2、5三种硬币我们就要查一下8-1、8-2、8-5也就是总额为7、总额为6和总额为3的最小硬币数是多少，这样加1就可以了，相当于补上了最后一块硬币。如果当前金额比你所有面值的金币要小，那就可以不用算了，因为你没法凑出来，在这里默认为float('inf')。

 　　这是自己写的代码，但是没有进行结构上的优化。

class Solution:
    def coinChange(self, coins, amount):
        dp = [0 for i in range(amount+1)] 
        for i in range(1,amount+1):
            min_num = float('inf')
            for num in coins:
                if i - num >= 0:
                    min_num = min(min_num,dp[i-num])
            dp[i] = min_num + 1
        return dp[amount] if dp[amount] != float('inf') else -1 

　　leetcode上面的官方的代码似乎还有些不同：

class Solution:
    def coinChange(self, coins: List[int], amount: int) -> int:
        dp = [float('inf')] * (amount + 1)
        dp[0] = 0
        
        for coin in coins:
            for x in range(coin, amount + 1):
                dp[x] = min(dp[x], dp[x - coin] + 1)
        return dp[amount] if dp[amount] != float('inf') else -1 

　　他第一层循环用的是硬币的种类，第二层循环从这个硬币的最小面值到目标面值，试图通过单一拿这个硬币来凑出来，也就是一个面值为5的凑成了5，两个我就把10也凑出来了，其他的先不动。下一轮我凑2的时候，顺理成章的5+2面值为7的也就凑出来了。也可以，但是还是我的牛逼一点。