机器学习算法理论基础

l1和l2的正则区别在哪里？

　　l1得到稀疏解可以用做特征选择，l2得到趋近于0的解可以防止过拟合。

　　l1正则项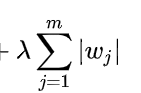：求导之后是λ

　　梯度下降法中梯度更新为 w：= w-aλ，此时a为常数，经过多次更新后w=0，从而正则化带来稀疏解。

　　l2正则项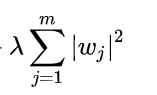：求导之后是2λw

 

　　梯度更新为w：=w-2aλw，因为衰减项中有w所以衰减中起到了减速的作用，多次迭代后趋近于0但是绝不会等于0。

 

 

　SVM支持向量机

 　　复习一下支持向量机相关的东西。

　　1.svm是个啥？有什么用？

　　　　svm是个二分类模型，本质是特征空间上间隔最大的线性分类器，学习策略就是间隔最大化，将二分类问题转化为一个求解凸二次规划的问题，等价于正则化的合页损失函数最小化问题。

　　2.上面说到的合页损失是什么？有什么特点？

　　

 

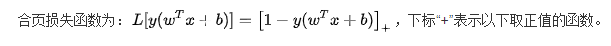
 　　　　特点是合页损失不仅要求正确分类，而且要求确信度尽量的高。也就是说这种损失对学习有更高的要求。

　　3.SVM的基本解法是什么？

 　　　　是解出能够正确划分数据集并且几何间隔最大的分类超平面，这个超平面是唯一的。训练完成后，最终模型仅与支持向量（位于最大间隔边界上的向量）有关。对于线性不可分的情况，使用软间隔方法引入松弛变量来进行求解。

　　　　简单流程：构造并求解凸二次规划问题，计算w*，求解分离超平面。

　　4.核函数是做什么用的？

　　　　将低维不可分的数据映射到高维特征空间，最终在高维特征空间中构造出最优的分离超平面。

　　5.都需要调节哪些参数？这些参数对模型有什么影响？

　　　　惩罚参数C：调节优化方向中指标的偏好程度。（间隔大小更重要还是分类准确度更重要）C过大则不允许存在误差样本，会过拟合；C趋近于0则认为间隔越大越好，欠拟合。

　　　　gama：对样本进行高维度映射，gama大效果好但是容易过拟合（决策平面可能是个花）gama小容易欠拟合（决策平面是个曲线）