格子刷油漆

试题 历届试题 格子刷油漆

 

【资源限制】  时间限制：1.0s   内存限制：256.0MB

问题描述

　　X国的一段古城墙的顶端可以看成 2*N个格子组成的矩形（如下图所示），现需要把这些格子刷上保护漆。


　　你可以从任意一个格子刷起，刷完一格，可以移动到和它相邻的格子（对角相邻也算数），但不能移动到较远的格子（因为油漆未干不能踩！）
　　比如：a d b c e f 就是合格的刷漆顺序。
　　c e f d a b 是另一种合适的方案。
　　当已知 N 时，求总的方案数。当N较大时，结果会迅速增大，请把结果对 1000000007 (十亿零七) 取模。

输入格式

　　输入数据为一个正整数（不大于1000）

输出格式

　　输出数据为一个正整数。

样例输入

2

样例输出

24

样例输入

3

样例输出

96

样例输入

22

样例输出

359635897

---

 

解题思路

　　在矩形的长度大于2的时候有两种情况：     1.从两边上的四个格子开始出发       2.从中间开始出发

　　

　　首先分析第一种情况（从两边上的四个格子开始出发）：

　　(由于四个格子都在最边上，没有差别，因此分析一个格子的所有情况乘以4即可得到从边上出发的情况总和。)

 

从最边上走有三种走法：（方式是我胡写的）

 

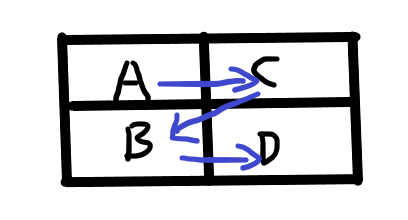
①不回头式

把本列都走过再走下一列

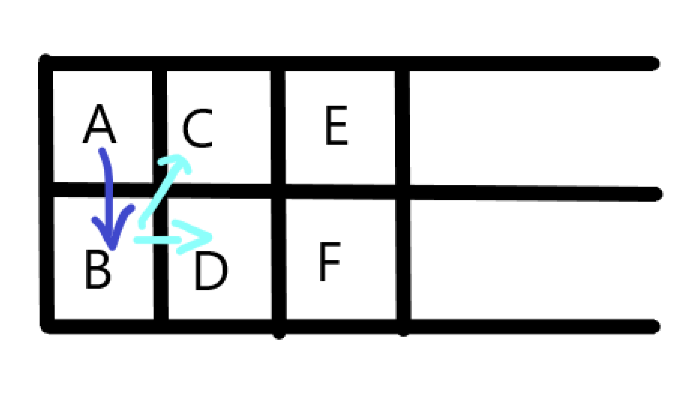
　　比如此图，从A开始出发，先走B，再走下一列，走到第二列的路线有两种，在i等于1的时候只有A到B一种走法，当i等于2的时候，i有1*2种走法，i等于3的时候有1*2*2种走法

　　 由此推出当在第i列的时候有a[i] = 2*a[i-1];

 

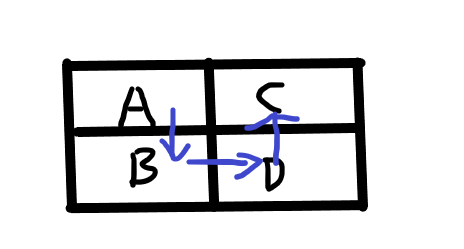
②返回式 

每次先走下一列，最后返回到开头相对的格子

　

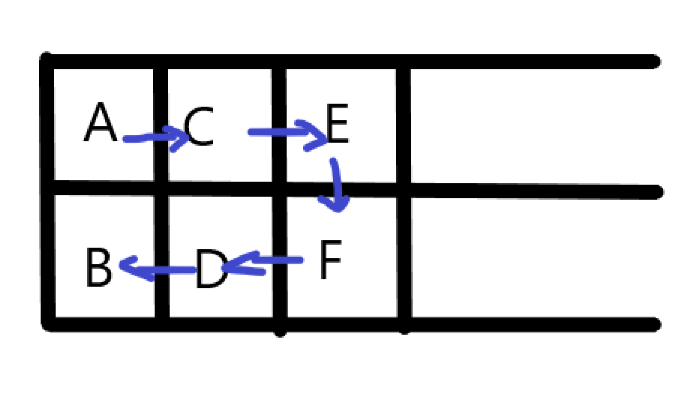
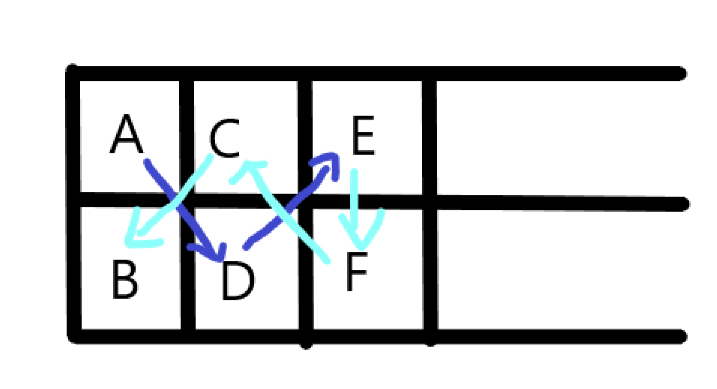
比如上两个图 从A点出发先到达C点或者D点 所以有b[i] = 2*b[i-1]  (由于此方式能返回到开始格子的对面，所以单独作为一种方式存储，在后面能用到)

 

 

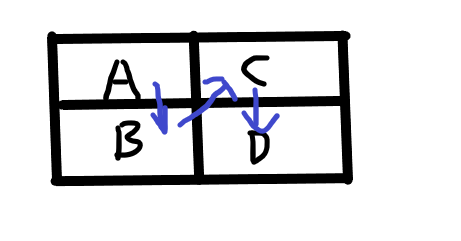
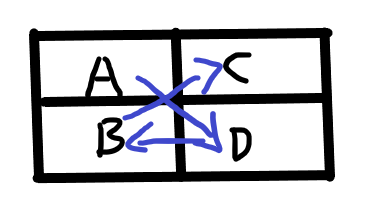
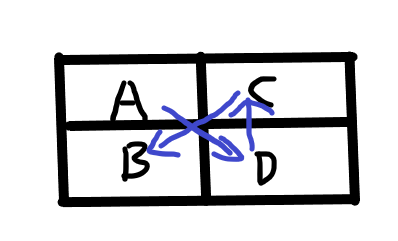
③一步一回头式

先走下一列，再返回上一列，再返回下一列的对面，然后再访问下一列 

　

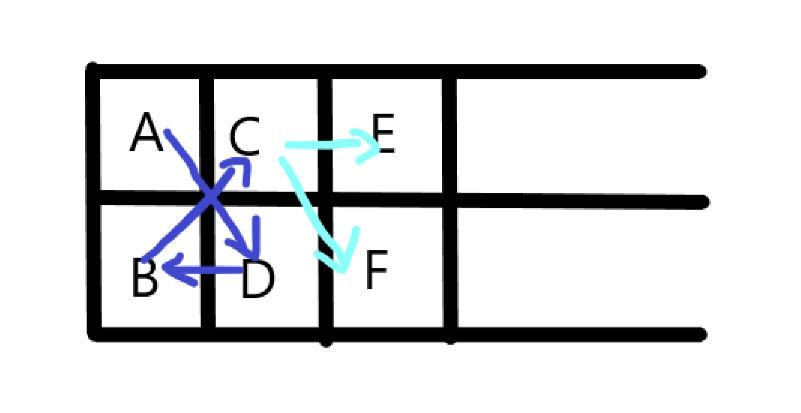
　　类似于上图这样子两种方式，然后到达E , F 自然有两种方式，所以推出 a[i] = 2*2*a[i-2]

　　所以第一种情况得出结论：a[i] = 2*a[i-1]+2*b[i-1]+4*a[i-2]

　　开头说过分析一个点，所以把四个点的都加起来就是  sum1 = 4*a[n]  //n代表列数

 

第二种情况（从中间格子开始出发）:

(此情况必须应用在N大于2的时候)

 

当从中间走的时候就将矩形分成了两部分，有先从左走和先从右走的区别（排列方式不一样）　　　

 

无论先从左走还是先从右走，先走的那一个方向必须能返回到当前格子的相对的格子，如果不能就返回不了了

这种方法我在上面提过，就是存储为b[i]的数组

 

从左边先走有两种方式（比如从A走）A -> C 和  A -> D两种

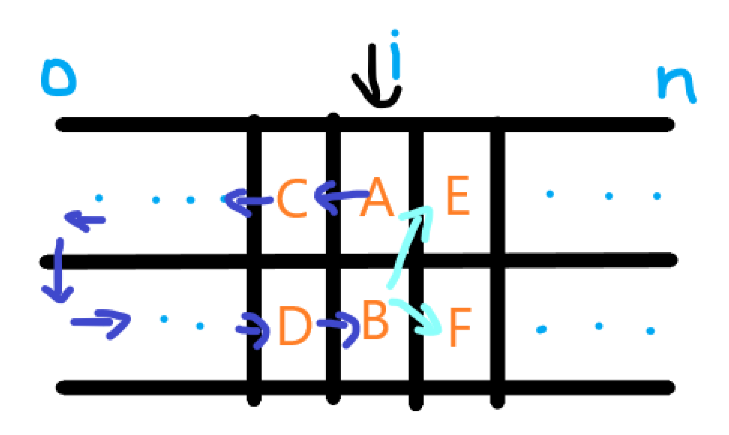
　　从A出发，最终到达B ，上面已经分析过 ， 有b[i]种方法

　　然后分析从E或者F走，从E或F走可以回头式的走，也可以一步走到头，跟从最边上点开始走的方式相同，此处避免冗余不再举例，不懂得可以再翻到头看，所以有a[n-i]种方法。

　　在第i列也可以从B走，与A走情况相同，结果乘以2即可，从B到E和F有两种方法，所以结果也要乘以2

　　因此总的走法有     2*2*(b[i]*a[i-1])

从右先走，与从左走是相颠倒的

　　从A往右走，最终返回B，有b[n-i+1]种方法，也可以从B出发，最终返回A，最终结果要乘以2

　　从B往左走有两种方法，到达D或C，所以结果也要乘以2

　　从E或F向左走，有a[i-1]种方法

　　所以从右先走右有2*2*（b[n-i]*a[i-1]）种走法

　　从左先走与从右先走加起来就是sum2 = 4*（b[i]*a[i-1]+b[n-i]*a[i-1]）

 　　　　

 

所以最终结果是sum1+sum2 = 4*a[n]+  4*（b[i]*a[i-1]+b[n-i]*a[i-1]）

　由于

a[i-2] 的结果 所以要给a[1]和a[2]赋值 从a[3]开始算，求a[3] 的时候需要求得b[2]，所以要给出a[1]、a[2]、b[1]、b[2]

当n a[1] = 1 , b[1] = 1  (实际为0，因为只有1列，没法算，这里改为1，是便于理解，实际没影响)

当n等于2的时候，只有从四个点开始的情况，所以罗列出来 a[2] = 6 , b[2] = 2;

　

            

                

---

代码：

import java.util.Scanner;

public class 格子刷油漆 {
    public static void main(String[] args) {
        int Mod = 1000000007;
        long[] a = new long[1001];
        long[] b = new long[1001];
        Scanner scanner = new Scanner(System.in);
        int N = scanner.nextInt();//列数
        a[1] = 1;
        b[1] = 1;
        a[2] = 6;
        b[2] = 2;
        if (N==1) {
            System.out.println("2");
        }
        if (N==2) {
            System.out.println(a[2]*4);
        }
        for (int i = 3; i <=N; i++) {//从头出发
            a[i] = (2*a[i-1]+2*b[i-1]+4*a[i-2])%Mod;
            b[i] = (2*b[i-1])%Mod;
        }
        long sum = 4*a[N]%Mod;
        for (int i = 2; i < N; i++) {//从中间出发，在2到N-1之间
            sum+=4*(b[i]*a[N-i]%Mod+b[N-i+1]*a[i-1]%Mod)%Mod;
            sum%=Mod;
        }
        System.out.println(sum);
    }
}

致谢

 　　思路借鉴CSDN博主 酱懵静  https://blog.csdn.net/the_ZED/article/details/104724184