94. 二叉树的中序遍历 ---- 递归、栈与回溯、颜色标记法make_pair

给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

 

示例 1：

 

 

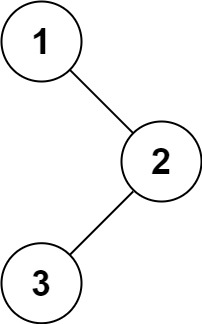
输入：root = [1,null,2,3]
输出：[1,3,2]
示例 2：

输入：root = []
输出：[]
示例 3：

输入：root = [1]
输出：[1]
 

提示：

树中节点数目在范围 [0, 100] 内
-100 <= Node.val <= 100
 

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

通过次数1,005,588提交次数1,321,391

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/binary-tree-inorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

 

递归：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    void inorder(TreeNode* root, vector<int>& res) {
        if (!root){ // 碰到空节点就 返回res
            return;
        }
        inorder(root->left, res);
        res.emplace_back(root->val);
        inorder(root->right, res);
    }
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        inorder(root, res);
        return res;
    }
};

栈与回溯：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;
        while(root != nullptr || !stk.empty()) {
            while (root != nullptr) {
                stk.push(root); // 左子树全部入栈
                root = root->left;
            } // 一直到向左子树蔓延至空节点结束
            root = stk.top(); // 若为空节点，回溯到上一节点
            stk.pop(); // 左下角叶子节点出栈
            res.emplace_back(root->val);
            root = root->right; // 指向刚刚回溯的节点的右节点 去判断是否为空，不为空就入栈出栈。
        }
        return res;
    }
};

 

 

 

Morris遍历的详细解释+注释版：来自评论

一些前置知识：

• 前驱节点，如果按照中序遍历访问树，访问的结果为ABC，则称A为B的前驱节点，B为C的前驱节点。
• 前驱节点pre是curr左子树的最右子树（按照中序遍历走一遍就知道了）。
• 由此可知，前驱节点的右子节点一定为空。

主要思想：

树的链接是单向的，从根节点出发，只有通往子节点的单向路程。

中序遍历迭代法的难点就在于，需要先访问当前节点的左子树，才能访问当前节点。

但是只有通往左子树的单向路程，而没有回程路，因此无法进行下去，除非用额外的数据结构记录下回程的路。

在这里可以利用当前节点的前驱节点，建立回程的路，也不需要消耗额外的空间。

根据前置知识的分析，当前节点的前驱节点的右子节点是为空的，因此可以用其保存回程的路。

但是要注意，这是建立在破坏了树的结构的基础上的，因此我们最后还有一步“消除链接”’的步骤，将树的结构还原。

重点过程： 当遍历到当前节点curr时，使用cuur的前驱节点pre

• 标记当前节点是否访问过
• 记录回溯到curr的路径（访问完pre以后，就应该访问curr了）

以下为我们访问curr节点需要做的事儿：

1. 访问curr的节点时候，先找其前驱节点pre
2. 找到前驱节点pre以后，我们根据其右指针的值，来判断curr的访问状态：

• pre的右子节点为空，说明curr第一次访问，其左子树还没有访问，此时我们应该将其指向curr，并访问curr的左子树
• pre的右子节点指向curr，那么说明这是第二次访问curr了，也就是说其左子树已经访问完了，此时将curr.val加入结果集中

更加细节的逻辑请参考代码：

 

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        TreeNode *predecessor = nullptr;

        while (root != nullptr) {
            if (root->left != nullptr) {
                // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止
                predecessor = root->left;
                while (predecessor->right != nullptr && predecessor->right != root) {
                    predecessor = predecessor->right;
                }
                
                // 让 predecessor 的右指针指向 root，继续遍历左子树
                if (predecessor->right == nullptr) {
                    predecessor->right = root;
                    root = root->left;
                }
                // 说明左子树已经访问完了，我们需要断开链接
                else {
                    res.push_back(root->val);
                    predecessor->right = nullptr;
                    root = root->right;
                }
            }
            // 如果没有左孩子，则直接访问右孩子
            else {
                res.push_back(root->val);
                root = root->right;
            }
        }
        return res;
    }
};

 颜色标记法：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<pair<TreeNode*, int> > stk;
        stk.push((make_pair(root, 0)));
        
        while(!stk.empty()) {
            auto [node, type] = stk.top();
            stk.pop();
            if(node == nullptr) continue;
            if(type == 0) {
                stk.push(make_pair(node->right, 0));
                stk.push(make_pair(node, 1));
                stk.push(make_pair(node->left, 0));
            }
            else result.emplace_back(node->val);
        }

        return result;

    }
};