790. 多米诺和托米诺平铺 （铺瓷砖问题）----- 动态规划，数学分析，递推寻找规律，求模

有两种形状的瓷砖：一种是 2 x 1 的多米诺形，另一种是形如 "L" 的托米诺形。两种形状都可以旋转。

 

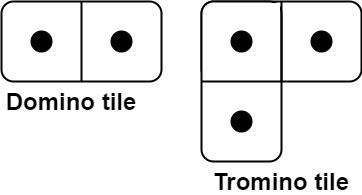
给定整数 n ，返回可以平铺 2 x n 的面板的方法的数量。返回对 109 + 7 取模 的值。

平铺指的是每个正方形都必须有瓷砖覆盖。两个平铺不同，当且仅当面板上有四个方向上的相邻单元中的两个，使得恰好有一个平铺有一个瓷砖占据两个正方形。

 

示例 1:

 

 

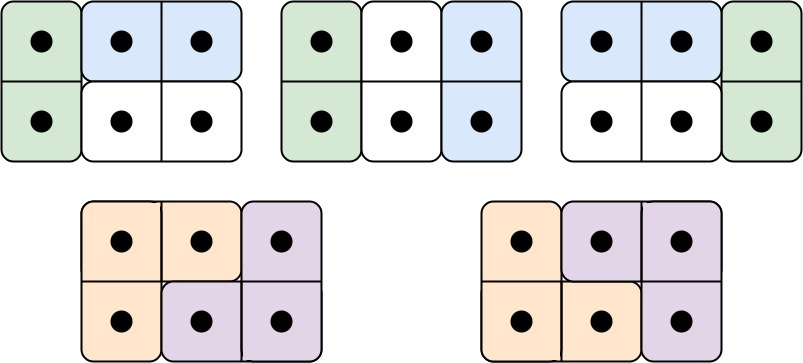
输入: n = 3
输出: 5
解释: 五种不同的方法如上所示。
示例 2:

输入: n = 1
输出: 1
 

提示：

1 <= n <= 1000

 

 

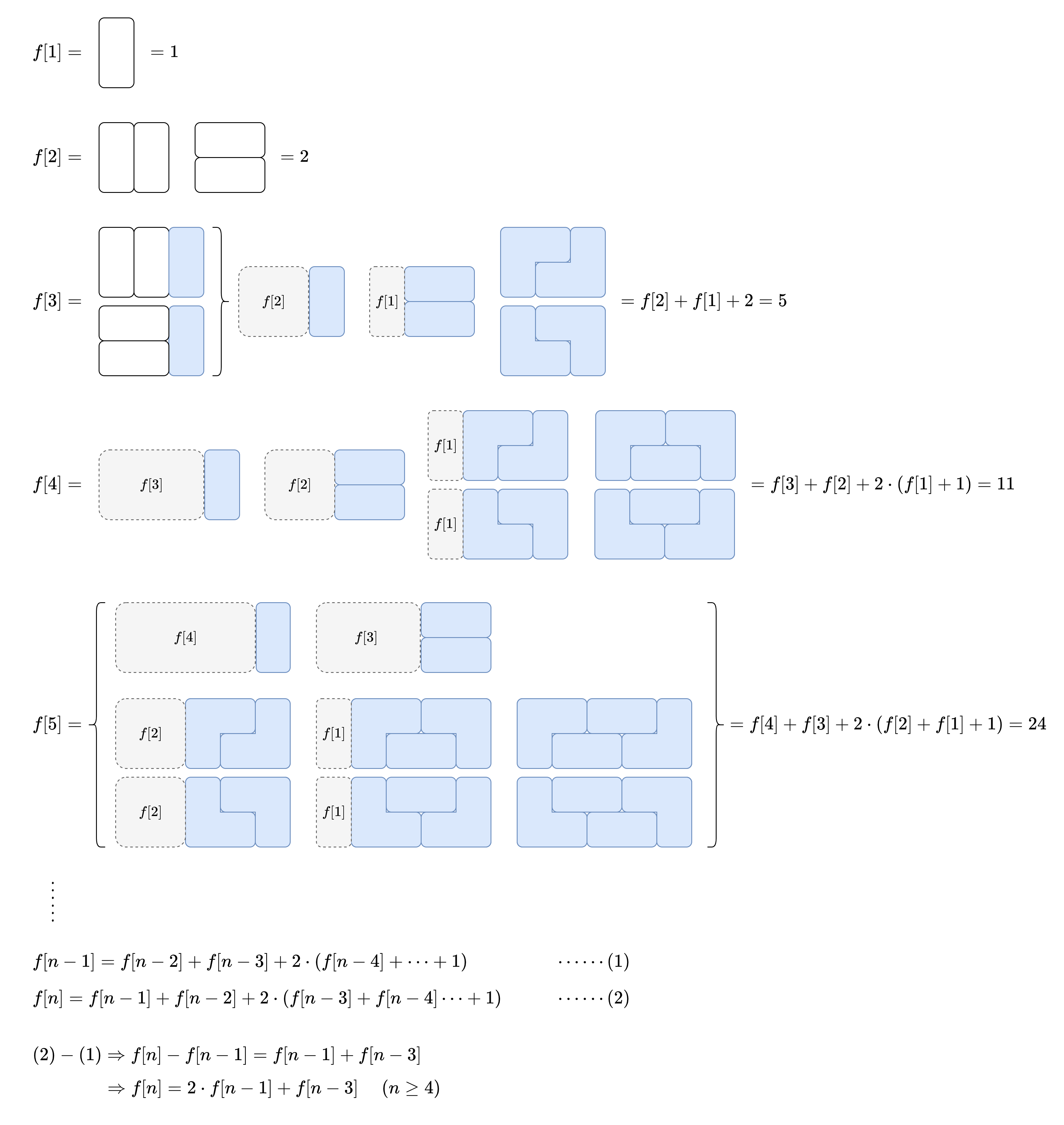
  图解来自 👉找不到规律？请看图！（Python/Java/C++/Go） - 多米诺和托米诺平铺 - 力扣（LeetCode）

class Solution {
    const int MOD = 1e9 +7;
public:
    int numTilings(int n) {
        vector<long> f;
        f.emplace_back(1);
        f.emplace_back(1);
        f.emplace_back(2);

        for (int i = 3; i <= n; ++i){
            f.emplace_back((2*f[i - 1] + f [i - 3]) %MOD);
        }
        return f[n];
    }
};