OO Unit1 Summary

一、程序结构分析

为了避免过于冗长，对于UML图中的方法和度量分析中的方法，我只截取了对于程序结构分析重要的方法，略去了部分不重要的方法(如get、set和部分add)。对于度量分析中的方法，我只截取了对于结构重要的方法和复杂度较高的方法来分析。

第一次作业

UML

Parse包的UML图

Expr包的UML图

Calc包的UML图

架构分析

总述

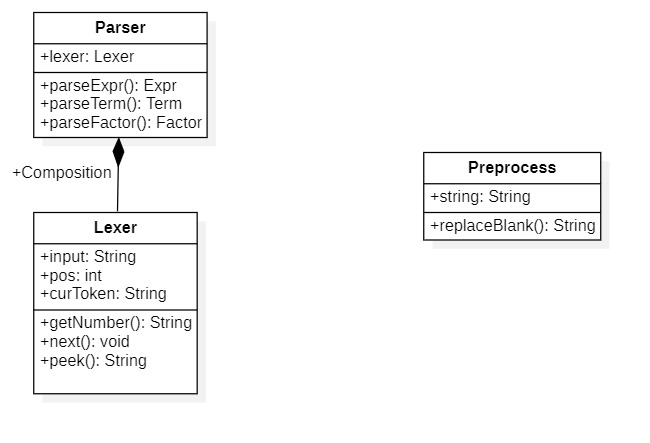
从流程上分析，求解作业主要分为两步：第一步是对表达式进行解析从而建立表达式各层次间的树状结构。第二步是基于已有的树状结构，转化为多项式结构，计算并化简。所以，我建立了三个包：Parser包的类用于对表达式进行预处理和解析表达式；Expr包的类用于描述表达式各层次的树状结构；Calc包的类用于描述表达式的多项式结构，计算和化简。通过将流程分布利于构建归属于不同流程的类群，同一类群中的类存在类之间的继承、实现等关系，不同类群中的类之间则不存在，这有助于降低类之间的耦合度。

Parser包

Parser包的重要属性是lexer对象，起到迭代器的作用。定义方法主要是对于表达式结构层次中各个类的parse()方法，通过递归下降法达到从线性结构向树状结构的转换。

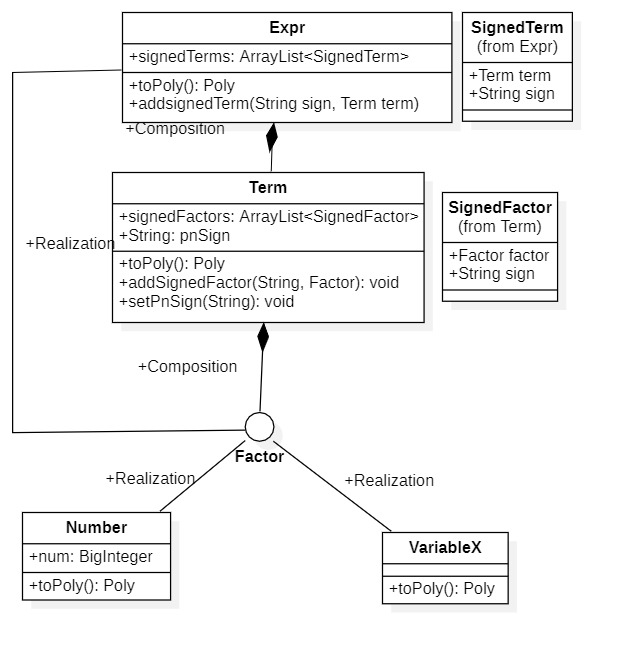
Expr包

对于Expr包中类，数据结构采用了ArrayList容器来描述。对于Expr包中的方法，主体是toPoly()方法，以实现从树状结构的到多项式结构的转换。

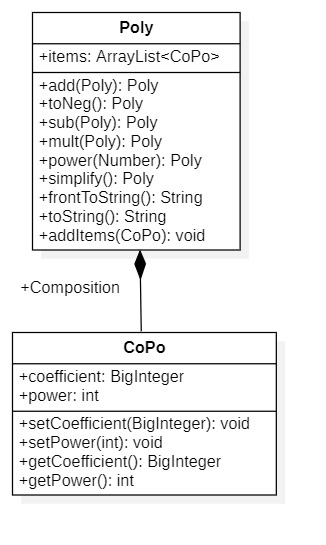
Calc包

Calc包的重要属性是CoPo对象，这是自定义的因子类，包含系数和指数，数据结构采用ArrayList容器描述。重要的方法是各类计算方法add()、sub()等，化简方法simplify()和输出方法toString().

优缺点分析

优点：层级结构鲜明，不同包之间耦合度低。
缺点：Calc包的Poly类过于庞大。

化简策略

为了提高程序性能，我采取了以下的化简策略：

去零项
合并同类项
将正数项提前

度量分析

Source File	Total Lines	Source code lines
CoPo.java	27	18
Expr.java	51	38
Factor.java	7	5
Lexer.java	50	42
MainClass.java	28	21
Number.java	28	20
Parser.java	89	76
Poly.java	208	185
PreProcess.java	21	17
Term.java	64	49
VariableX.java	14	11
Total	587	482

Code lines

可以发现Poly类的代码量较大，因为Poly需要集成各类运算方式及化简方式。其他类代码量较为正常。

class	OCavg	OCmax	WMC
MainClass	1.0	1.0	1.0
expr.VariableX	1.0	1.0	1.0
parse.PreProcess	1.5	2.0	3.0
expr.Number	1.0	1.0	5.0
calc.CoPo	1.0	1.0	6.0
expr.Expr	2.0	4.0	6.0
expr.Term	1.75	4.0	7.0
parse.Lexer	2.2	6.0	11.0
parse.Parser	3.5	5.0	14.0
calc.Poly	4.818181818181818	18.0	53.0

Class metrics

可以看到Poly类的平均方法复杂度较高，主要原因是我采用了将表达式类转化为多项式类的处理方式，所以Poly类需要从全局处理数据，这也就会导致这个类的方法复杂度较高。

其次Parser类的方法复杂度也较高。主要原因是递归下降法需要递归调用下一层次的方法，这决定了其本身复杂度不会太低。

Method	CogC	ev(G)	iv(G)	v(G)
calc.Poly.add(Poly)	2.0	1.0	3.0	3.0
calc.Poly.toNeg()	1.0	1.0	2.0	2.0
calc.Poly.sub(Poly)	0.0	1.0	1.0	1.0
calc.Poly.power(Number)	4.0	2.0	3.0	3.0
calc.Poly.mult(Poly)	3.0	1.0	3.0	3.0
calc.Poly.simplify()	11.0	3.0	7.0	7.0
calc.Poly.toString()	31.0	6.0	16.0	18.0
expr.Expr.toPoly()	5.0	1.0	4.0	4.0
expr.Term.toPoly()	6.0	1.0	5.0	5.0
expr.VariableX.toPoly()	0.0	1.0	1.0	1.0
parse.Lexer.getNumber()	2.0	1.0	3.0	3.0
parse.Lexer.Lexer(String)	0.0	1.0	1.0	1.0
parse.Lexer.next()	7.0	2.0	5.0	6.0
parse.Lexer.peek()	0.0	1.0	1.0	1.0
parse.Parser.parseExpr()	5.0	1.0	5.0	5.0
parse.Parser.parseFactor()	9.0	3.0	5.0	6.0
parse.Parser.parseTerm()	4.0	1.0	5.0	5.0
parse.PreProcess.replaceBlank()	2.0	2.0	2.0	2.0
calc.Poly.frontToString(StringBuilder, int)	18.0	1.0	12.0	12.0
...	...	...	...	...
Total	113.0	64.0	119.0	123.0
Average	2.173076923076923	1.2307692307692308	2.2884615384615383	2.3653846153846154

Method metrics

Poly类的toString()方法的极高复杂度，还因为第一次作业中的toString()方法采用了多次if-else的结构来判断并进行输出，这种方法虽然逻辑较为简单，但是具体coding过程十分繁琐，以至于我为了实现toString()转化又做了一个frontToString()方法，同样具有很高的复杂度。需要在实现逻辑上进行修改。

所幸其他方法的基本复杂度ev(G)和模块设计复杂度iv(G)都为正常水平。iv(G)值小说明类耦合度较低。

第二、三次作业

因为我第二次作业的构架较为利于第三次作业的开发，所以第三次作业时我只在Poly类中增加了一个方法且对其他Poly类的方法进行了微调，与第二次作业没有结构上的区别。所以我将第二、三次作业放到一起分析程序结构。

UML

Parse包的UML图

Expr包的UML图

Calc包的UML图

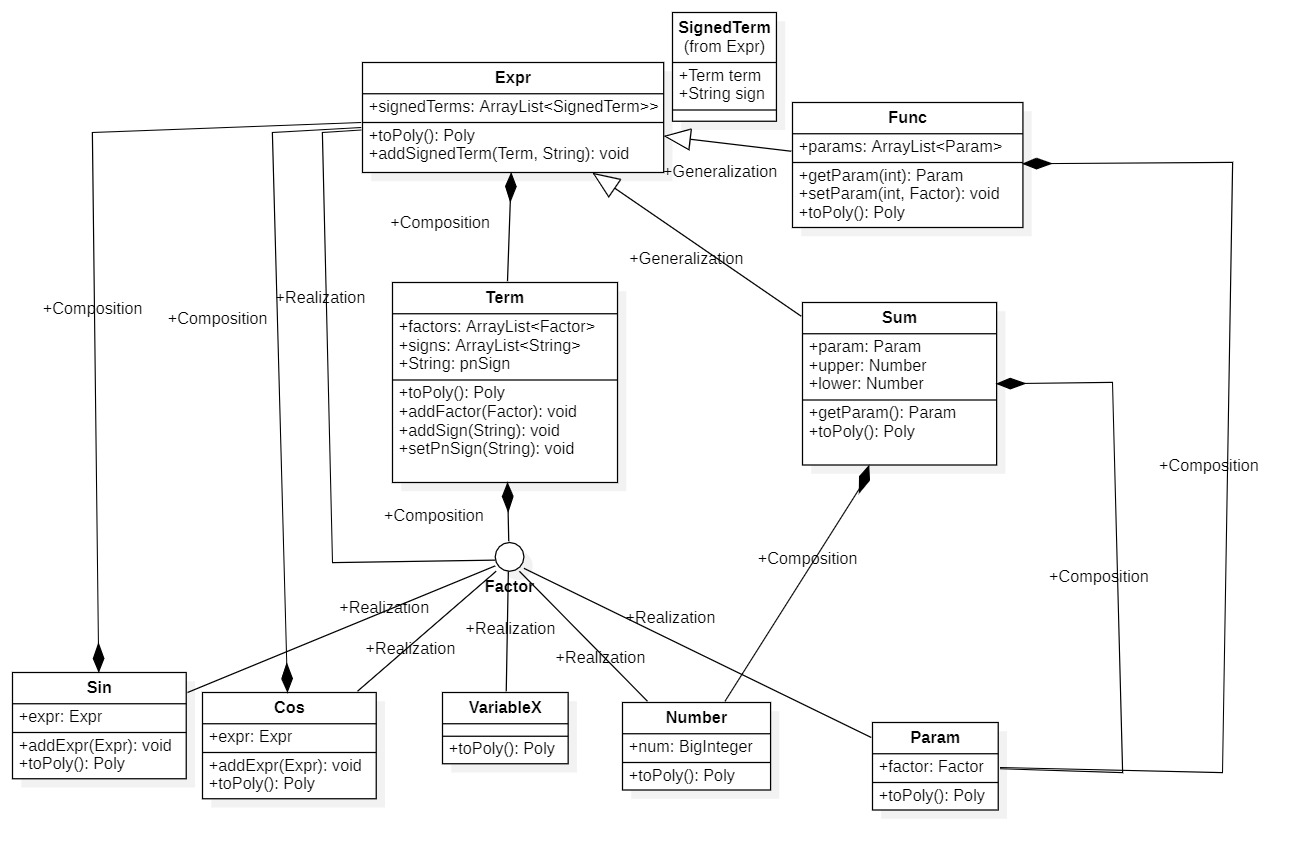
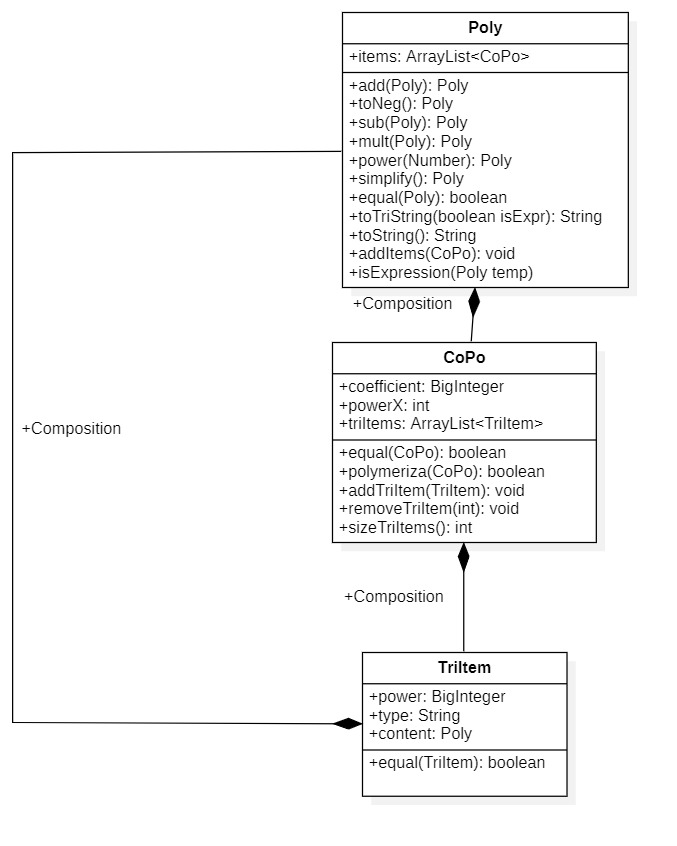
架构分析

总述

第二、三次作业的流程不变，这三个包仍然能支持，需要做的是根据需求扩充三个包的内容。包括新增类，新增类的方法、属性等。

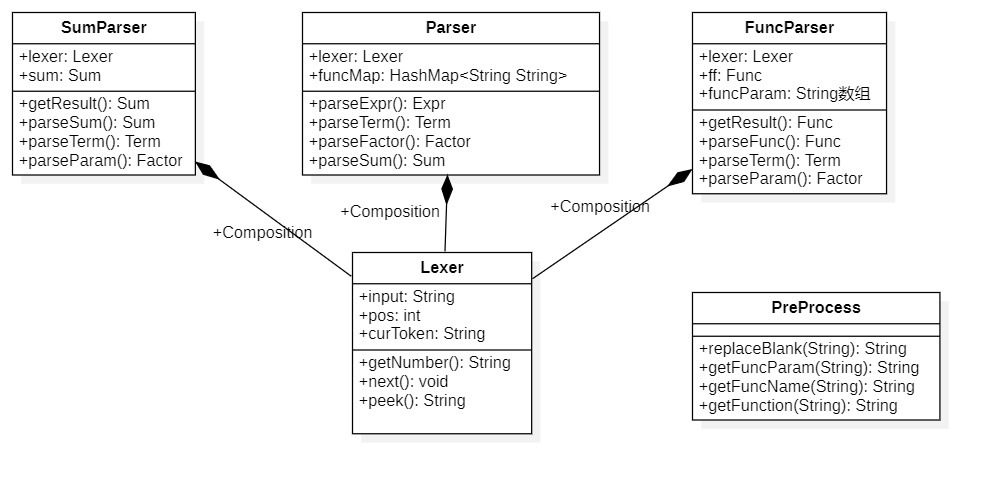
Parser包

针对新增的自定义函数和求和函数的需求，我新增了两个Parser分别针对于这两种数据的解析，两个Parser的内部实现与起初的Parser大同小异。同时，我将PreProcessing的属性取消，也就是PreProcess类完全成为了方法类。

Expr包

第二、三次作业需要增加三角函数类、自定义函数类和求和函数类，此外，为了实现参数代入，我设计了Param类。Param类之所以采用实现Factor接口并且再添加一个Factor对象的看似有些奇怪操作，是由于我的自定义函数代入实参的方法所要求的。对于代入实参，这里我与其他同学的在Expr、Term、Factor每一层实现replace方法不同，我选择的方法是让自定义函数的所有同一名字的形参共用一个Param对象，这样在实现代入实参的操作时只需要将该Param对象赋值即可！这样处理的优点在于代入操作十分便捷，缺点在于实现定义一个共用Param对象的自定义函数对象是比较复杂的。所以这也就是我Parser包要新增Parser类的原因。自定义函数Parser不仅要实现对自定义函数的解析，还要产生我所要求的自定义函数对象。

Calc包

由于二、三次作业要求新增三角函数类，所以我在CoPo类中新增了三角函数类TriItem的ArrayList来处理。而TriItem类的其中一个属性是多项式类Poly，这对应的是三角函数的内容可以是多项式。从而Calc包中的多项式结构也形成了递归层次。

优缺点分析

优点：层级结构鲜明，不同包之间耦合度低。
缺点：Calc包的Poly类过于庞大，Parse包的三个Parser具有部分重复的方法，略显臃肿。

化简策略

去零项
将sin(0)化为0，cos(0)化为1，引入平方和公式
合并同类项

度量分析

Source File	Total Lines	Source Code Lines
CoPo.java	90	72
Cos.java	33	27
Expr.java	75	58
Factor.java	9	6
Func.java	24	18
FuncParser.java	124	105
Lexer.java	76	66
MainClass.java	51	29
Number.java	31	23
Param.java	29	22
Parser.java	160	131
Poly.java	502	457
PreProcess.java	40	33
Sin.java	34	27
Sum.java	69	58
SumParser.java	119	102
Term.java	69	58
TriItem.java	57	45
VariableX.java	16	12
Total	1608	1349

Code lines

可以看到，第二、三次作业依然是Poly类代码量较大，原因前文已经提过，此处不再赘述。

Class	OCavg	OCmax	WMC
parse.SumParser	3.6	8.0	18.0
parse.PreProcess	1.2	2.0	6.0
parse.Parser	3.8333333333333335	12.0	23.0
parse.Lexer	2.4285714285714284	10.0	17.0
parse.FuncParser	3.8	9.0	19.0
MainClass	2.0	2.0	2.0
expr.VariableX	1.0	1.0	2.0
expr.Term	1.8333333333333333	5.0	11.0
expr.Sum	1.25	3.0	10.0
expr.Sin	1.0	1.0	3.0
expr.Param	1.2	2.0	6.0
expr.Number	1.2	2.0	6.0
expr.Func	1.3333333333333333	2.0	4.0
expr.Expr	1.5714285714285714	4.0	11.0
expr.Cos	1.0	1.0	3.0
calc.TriItem	1.2222222222222223	2.0	11.0
calc.Poly	4.625	17.0	111.0
calc.CoPo	1.4666666666666666	8.0	22.0

Class metrics

可以看到Poly类复杂度较高，是因为第二、三次作业的数据结构变复杂了，且定义了更多的化简方法。同时Parser类复杂度较高，主要是因为它要承担更复杂的项的解析任务。

Method	CogC	ev(G)	iv(G)	v(G)
calc.CoPo.addTriItem(TriItem)	0.0	1.0	1.0	1.0
calc.CoPo.equal(CoPo)	1.0	1.0	2.0	2.0
calc.CoPo.polymeriza(CoPo)	18.0	6.0	10.0	10.0
calc.CoPo.removeTriItem(int)	0.0	1.0	1.0	1.0
calc.CoPo.sizeTriItems()	0.0	1.0	1.0	1.0
calc.Poly.add(Poly)	0.0	1.0	1.0	1.0
calc.Poly.addItem(CoPo)	0.0	1.0	1.0	1.0
calc.Poly.appendFirstPartOfTri(StringBuilder, ArrayList, int)	5.0	1.0	5.0	5.0
calc.Poly.equal(Poly)	23.0	5.0	13.0	13.0
calc.Poly.isExpression(Poly)	11.0	1.0	10.0	11.0
calc.Poly.mult(Poly)	3.0	1.0	3.0	3.0
calc.Poly.power(Number)	4.0	2.0	3.0	3.0
calc.Poly.simplify()	11.0	4.0	4.0	6.0
calc.Poly.simplify1(Poly)	13.0	1.0	7.0	7.0
calc.Poly.simplify2(Poly)	14.0	6.0	6.0	7.0
calc.Poly.simplify3Cos(Poly)	12.0	3.0	6.0	6.0
calc.Poly.simplify3Sin(Poly)	12.0	3.0	6.0	6.0
calc.Poly.simplify4(Poly)	8.0	1.0	5.0	5.0
calc.Poly.simplifyCos()	3.0	3.0	3.0	3.0
calc.Poly.simplifyNone()	3.0	3.0	3.0	3.0
calc.Poly.simplifySin()	3.0	3.0	3.0	3.0
calc.Poly.sub(Poly)	0.0	1.0	1.0	1.0
calc.Poly.toNeg()	1.0	1.0	2.0	2.0
calc.Poly.toString()	57.0	1.0	19.0	19.0
calc.Poly.toTriString(boolean)	58.0	1.0	20.0	20.0
calc.TriItem.equal(TriItem)	1.0	1.0	3.0	3.0
expr.Cos.toPoly()	0.0	1.0	1.0	1.0
expr.Expr.toPoly()	5.0	1.0	4.0	4.0
expr.Func.setParam(int, Factor)	0.0	1.0	1.0	1.0
expr.Number.toPoly()	1.0	2.0	1.0	2.0
expr.Param.toPoly()	0.0	1.0	1.0	1.0
expr.Sin.toPoly()	0.0	1.0	1.0	1.0
expr.Sum.toPoly()	4.0	2.0	3.0	3.0
expr.Term.changePnSign(String)	0.0	1.0	1.0	1.0
expr.Term.toPoly()	10.0	1.0	6.0	6.0
expr.VariableX.toPoly()	0.0	1.0	1.0	1.0
parse.FuncParser.getResult()	0.0	1.0	1.0	1.0
parse.FuncParser.parseFunc()	5.0	1.0	5.0	5.0
parse.FuncParser.parseParam()	15.0	7.0	11.0	12.0
parse.FuncParser.parseTerm()	4.0	1.0	5.0	5.0
parse.Lexer.getNumber()	2.0	1.0	3.0	3.0
parse.Lexer.next()	17.0	2.0	10.0	13.0
parse.Lexer.peek()	0.0	1.0	1.0	1.0
parse.Parser.parseExpr()	5.0	1.0	5.0	5.0
parse.Parser.parseFactor()	20.0	10.0	14.0	15.0
parse.Parser.parseSum()	0.0	1.0	1.0	1.0
parse.Parser.parseTerm()	4.0	1.0	5.0	5.0
parse.PreProcess.getFuncName(String)	0.0	1.0	1.0	1.0
parse.PreProcess.getFuncParam(String)	0.0	1.0	1.0	1.0
parse.PreProcess.getFunction(String)	0.0	1.0	1.0	1.0
parse.PreProcess.replaceBlank(String)	2.0	2.0	2.0	2.0
parse.SumParser.getResult()	0.0	1.0	1.0	1.0
parse.SumParser.parseParam()	12.0	6.0	8.0	9.0
parse.SumParser.parseSum()	5.0	1.0	5.0	5.0
parse.SumParser.parseTerm()	4.0	1.0	5.0	5.0
...	...	...	...	...
Total	386.0	179.0	319.0	331.0
Average	3.1129032258064515	1.4435483870967742	2.5725806451612905	2.6693548387096775

Method metrics

可以发现，复杂度和耦合度较高的方法主要集中在Poly包中的类和Parser包中的类，这是主要是因为这两个类聚合了较多的方法，且方法的复杂度都较高。分析原因：Poly包中类的复杂度较高主要还是前文所说的要对全局的数据进行操作，难免会导致复杂度偏高；同时由于使用了ArrayList作为数据结构，导致化简操作定义了一系列复杂度高的方法，这点是我的失败之处。如果采用HashMap或许会极大简化化简流程。Parser类的复杂度高主要还是前文所说的递归下降法本身复杂的原因。

小总结

总的来说，Unit1的作业采用的一些策略有利也有弊。

将计算部分与结构部分分离(就是使用了Poly包和Expr包两块)
- 优点：使得流程划分清晰，逻辑上更畅通。方便后续进行白盒测试。
- 缺点：计算部分庞大，方法复杂度和耦合性都较高。
- 总的来说流程划分上偏向于面向过程的思维，但个人感觉无可厚非，毕竟面向过程和面向对象不是对立的，而应该相辅相成服务于编程。
使用ArrayList容器而非HashMap容器
- 优点：非常直白的建立了易于理解的数据结构。
- 缺点：给化简部分增添了较大的困难，导致其复杂度偏高。
- 总的来说使用HashMap容器或许能取得更好的效果。
采用了并非replace的自定义函数参数带入方法
- 优点：不需要在Expr包中各个类增添replace方法。
- 缺点：给解析部分创造了较大困难，导致其复杂度偏高。
- 总的来说利弊相抵。

二、bug分析

我在三次强侧和互测中都没有出现bug。不过我愿意就写程序时的防止出现bug的方法进行阐述。

总的来说，我采用了白盒测试和黑盒测试结合的方法进行测试。

白盒测试：对于互相耦合度较高的类群，可以构造针对这一类群的数据检验其输入和输出。白盒测试的意义在于当确保了当前模块的正确性以后，后续程序出现bug后可以忽略这一部分的检查。
黑盒测试：针对整个程序进行测试。主要有边界数据测试和随机数据测试两种方法。
- 边界数据测试：主要针对作业指导书中特别提到的情况进行测试。
- 随机数据测试：在第三次作业时，我借助Python的Sympy库建立了自动评测机，能够实现随机数据生成和正确性检验两个功能(但不具备全自动化功能，所以需要手动run)。我使用我构建的自动评测机完成了随机数据测试。这里展示部分我的自动评测机代码。

    # 随机数据生成部分：生成Factor
    def getFactor(self):
        global f, g, h
        global MultFunc

        type = self.rd(1, 6)

        if (type == 1):
            sympStr, sympExpr = self.getPowerX()
            return sympStr, sympExpr

        elif (type == 2):
            sympStr, sympExpr = self.getTri()
            return sympStr, sympExpr

        elif (type == 3):
            sympStr, sympExpr = self.getNumber()
            return sympStr, sympExpr

        elif (type == 4):
            sympStr, sympExpr = self.getExpr()
            expoStr, expoExpr = self.getExponent()
            sympStr = "(" + sympStr + ")" + "**" + expoStr
            sympExpr = sympExpr ** expoExpr
            return sympStr, sympExpr

        elif (type == 5):
            s = Sum()
            sympStr, sympExpr = Sum.getSum(s)
            return sympStr, sympExpr

        elif (type == 6):
            rdnum = self.rd(1,3)
            factor1str, factor1expr = self.getFactor()
            factor2str, factor2expr = self.getFactor()
            if (rdnum == 1):
                sympExpr = f.subs(y, factor1expr)
                sympExpr = sympExpr.subs(z, factor2expr)
                sympStr = "f(" + factor1str + "," + factor2str + ")"
            elif (rdnum == 2):
                sympExpr = g.subs(y, factor1expr)
                sympExpr = sympExpr.subs(z, factor2expr)
                sympStr = "g(" + factor1str + "," + factor2str + ")"
            else:
                sympExpr = h.subs(y, factor1expr)
                sympExpr = sympExpr.subs(z, factor2expr)
                sympStr = "h(" + factor1str + "," + factor2str + ")"
            return sympStr, sympExpr
        
# 正确性验证部分
from sympy import Symbol

x = Symbol('x')
str = #... for Java input
myTested = #... Java output
standard = #... Python standard result
print(standard.equals(myTested)) #... test

三、hack策略

我在第一次和第二次互测中测出了分别hack出了一个bug，第三次互测中没有hack出bug。

互测的策略主要是浏览代码加黑盒测试。

技巧是浏览代码看大体逻辑，这时一般通过捷径处理的操作是很容易观察到的。比如在第二次互测中，我发现同房间的一个同学在化简操作时直接将x**1替换为x，那么这个时候就可以通过构造x的十几次幂的结果来hack成功。

黑盒测试是人工构造数据和随机生成数据来测试。

构造数据的技巧是针对我自己在完成本次作业中感到处理困难的地方设计数据，比如在第一次作业中，我感到多个加减号与空白符穿插共存的情况可能会较难处理，因此在第一次互测时设计了相应的数据并hack成功。

第三次互测之所以没测出bug主要原因有三：

自动评测机没有实现全自动化测评功能，导致手动run还是较为耗时。
第二次到第三次的迭代较为顺利，所以没有较为困难处理的经历。
第三次互测房中只有一人被互测测出bug，而我阅读代码的重点放在了其他人身上。(泪目)

四、架构设计体验及心得体会

架构设计体验

总的来说，三次作业的迭代开发是比较顺利的，没有经过大规模重构。我认为有两点秘诀：

建立最贴合逻辑的类之间的层次关系。
最简明的方式处理细节。

第一点：何谓合逻辑，我认为是最大程度上保持了实际问题与coding的一一映射。比如对于多项式类的处理：一个多项式很显然可以划分为多个项，ArrayList容器能够实现一一映射，那么ArrayList容器就是合逻辑的，解决这个问题就可以用ArrayList。且由于逻辑上的一一映射，那么化简步骤是一定可以实现的，只是相较于HashMap复杂一些罢了。

第二点：何谓简明，我认为越简单解决问题的方式是越优的。比如说第一次作业的空白符的问题。对于空白符，我的处理是直接采用正则表达式匹配替换的操作，而不是在解析的时候再去跳跃空白符。再比如加减号重复出现的问题，我处理的方式是在Expr类中同时储存符号的ArrayList，而不是预处理字符串。只要我使用的方式是简明的，那么正确性就会有极高的保证。

心得体会

虽然在开发中我没有经过重构，过程比较顺利，但不得不说，写作业的过程还是挺艰难的。最痛苦的时候是第一周，在刚拿到这个作业的时候是一头雾水，经过好几天的思索也没能在整体流程上完成构思，这让我很痛苦。多亏了助教和同学们的帮助我才能完成第一周的作业。之后第二、三周的作业也是经过了个人的反复探索和推倒重来，才得以完成作业。

之前没有Java语言的基础，第一次接触Java编程和OO的思想，我感到收获颇多，完成了一轮没有被hack过的project，我还是挺开心的\doge。

五、一点反馈

我的第一周作业，当时不会的时候是真不会啊！真的是运气比较好，受到了助教和同学们的帮扶，我才得以磕磕绊绊地完成。我想如果课程上能够针对作业提供更多思路上的引导，并且对于难点步骤给予更多的预习资料或课上讲解，我相信效果会更好。

思路上的引导：比如说第一次作业，可以适当点拨一下分为解析、计算流程，计算流程用什么样的方法去描述加法，又用什么样的方法去描述乘法。

难点步骤：比如说递归下降法，个人认为可以将该部分内容提到pre中去，使得同学们能有充分时间准备。

posted @ 2022-03-23 19:03 SleepEarlyGuy 阅读(78) 评论(2) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

sleepEarlyGuy

OO Unit1 Summary

OO Unit1 Summary

目录

一、程序结构分析

第一次作业

UML

架构分析

总述

Parser包

Expr包

Calc包

优缺点分析

化简策略

度量分析

第二、三次作业

UML

架构分析

总述

Parser包

Expr包

Calc包

优缺点分析

化简策略

度量分析

小总结

二、bug分析

三、hack策略

四、架构设计体验及心得体会

架构设计体验

心得体会

五、一点反馈

公告