数据结构笔记 — 树
树
1.1 树的概念
-
树
(Tree)是n(n>=0)个结点的有限集,当n=0时成为空树,在任意一棵非空树中-
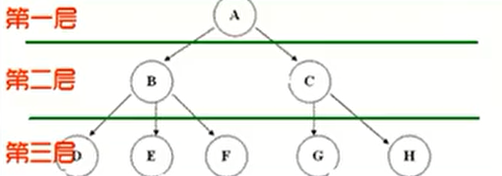
有且仅有一个 特定的称为根
(Root)的结点 -
当
n>1时,其余结点可分为m(m>0)个互不相交的有限集1、T2、..、Tm,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)![]()
-
-
每一个圈称为树的一个 结点 ,结点拥有的子树数称为 结点的度 (Degree) ,树的度取树内各结点的度的 最大值
-
度为
0的结点称为叶结点(Leaf)或终端结点 -
度不为
0的结点称为分支结点点或非终端结点,除根结点外,分支结点也称为内部结点![]()
-
-
节点间关系
-
结点的子树的根称为结点的孩子
(Child),相应的,该结点称为孩子的双亲(Parent),同一双亲的孩子之间互称为兄弟(Sibling) -
结点的祖先是从根到该结点所经分支上的所有结点
-
-
结点的层次
-
结点的层次
(Level)从根开始,根为第一层,根的孩子为第二层 -
其双亲在同一层的结点互为堂兄弟
-
树中结点的最大层次称为树的深度
(Depth)或高度![]()
-
-
如果将树中结点的各子树看成从左至右是有次序的,不能互换的,则称该树为有序树,否则称为无序树
-
森林
(Forest)是m(m>=0)棵互不相交的树的集合。对树中每个结点而言,其子树的集合即为森林
1.2 树的结构及表示
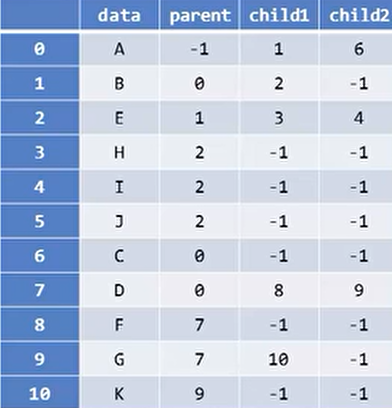
双亲表示法
#define MAX_TREE_SIZE 100 typedef int ElemType ; typedef struct PTNode{ ElemType data; //结点数据 int parent; //双亲位置 } PTNode; typedef struct { PTNode nodes[MAX_TREE_SIZE]; int r; //根的位置 int n; //结点数目 } PTree;
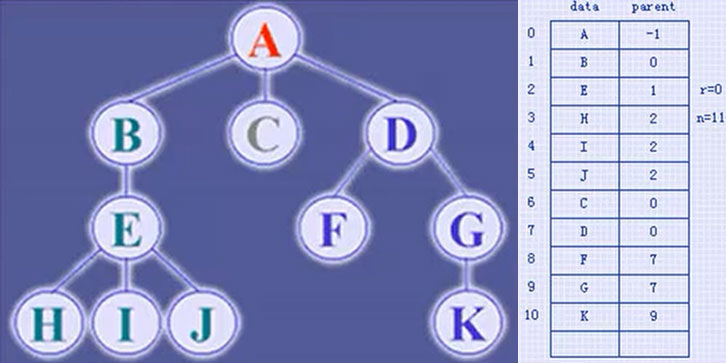
-
此种表示法中,我们可以根据某节点的
parent指针找到其双亲结点,时间复杂度为O(1),当做一年到parent == 1时,表示找到了树的根节点 -
但是,如果想要知道某结点的孩子,那么只能遍历整个树,此时,应当改变一下表示方法
![]()
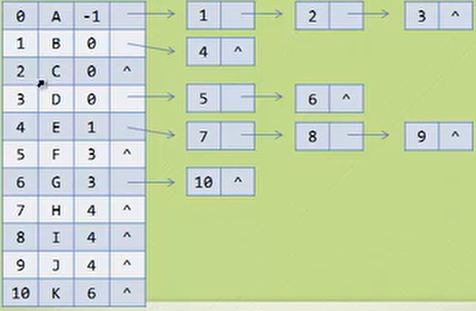
孩子表示法
-
每个结点的指针指向一个链表,链表中存放的是其孩子结点所对应的的下标值
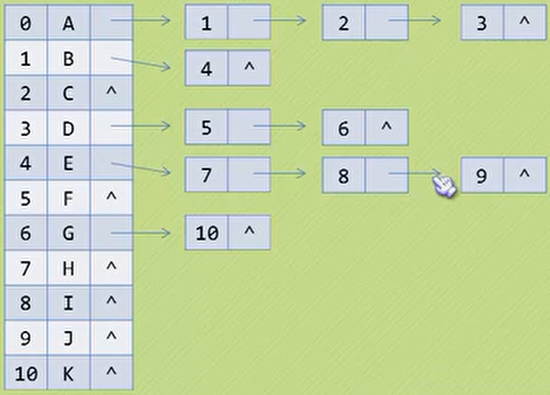
孩子双亲表示法
-
将上方的孩子表示法进行完善,加入每个结点的双亲所对应的下标即可
![]()
#include <stdio.h> #define MAX_TREE_SIZE 100 typedef char ElemType; //孩子结点 typedef struct CTNode{ int child; //孩子结点的下标 struct CTNode *next; //指向下一孩子结点的指针 } *ChildPtr; //表头结构 typedef struct { ElemType data; //存放树中结点的数据 int parent; //存放双亲的下标 ChildPtr firstChild; //指向第一个孩子的指针 } CTBox; //树结构 typedef struct { CTBox nodes[MAX_TREE_SIZE]; //结点数组 int root, num; //根节点和节点数量 } CTree;
2 二叉树
-
二又树
(Bnary Tree)是n(n>=0)个结点的有限集合,该集合或者为空集(空二又树),或者由一个根结点和两棵互不相交的、分别称为根结点点的左子树和右子树的二又树组成 -
二叉树特点
-
每个结点最多有两棵子树,所以二又树中不存在度大于
2的结点 -
左子树和右子树是有顺序的,次序不能颠倒
-
即使树中某结点只有一棵子树,也要 区分它是左子树还是右子树
-
-
斜树:均为左子树或者均为右子树
-
满二叉树 :在一棵二又树中,如果所有分支结点 都存在左子树和右子树 ,并且 所有叶子都在同一层 上,这样的二又树称为满二又树
-
特点
-
叶子只能出现在最下一层
-
非叶子结点的度一定是
2 -
在同样深度的二又树中,满二又树的结点个数一定最多,同时叶子也是最多
![]()
-
-
-
完全二叉树 :对一棵具有
n个结点的二又树按层序编号,如果编号为i(1<=i<=n)的结点与同样深度的满二又树中编号为i的结点点位置完全相同,则这棵二叉树称为完全二又树
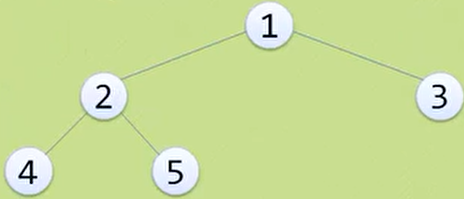
-
-
叶子结点只能出现在最下两层
-
最下层的叶子一定集中在左部连续位置
-
倒数第二层,若有叶子结点,一定都在右部连续位置
-
如果结点度为
1,则该结点只有左孩子 -
同样结点树的二又树,完全二又树的深度最小
-
满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树
-
-
二叉树的性质
-
二叉树的第
i层至多有 个结点(i >= 1) -
深度为
k的二叉树至多有 个结点(k >= 1) -
对于任意一棵二叉树
T,如果其终端结点数为 ,度为2的结点数为 ,则 n0 = n1 + 1 ![]()
-
-
-
如果对一棵拥有
n个结点的完全二叉树(深度为)的结点按照层序编号,对于任意结点i(1 <= i <= n)具有以下性质:-
如果
i = 1,则结点i是二叉树的根,无双亲 -
如果
i > 1,则其双亲是结点 [ i / 2] (下限取整) -
如果
2i > n,则结点i无左孩子(结点i为叶子结点 ),否则其左孩子是结点2i -
如果
2i+1 > n,则结点i无右孩子,否则其右孩子是结点2i+1
-
-
-
结构定义
typedef struct BitNode{ ElemType data; struct BitNode *lChild, *rChild; } BiTNode, *BiTree;
-
二叉树的遍历:
(traversing binary tree)是指从根结点出发,按照某种 次序 依次 访问 二又树中所有结点,使得 每个结点被访问一次且仅被访问一次 -
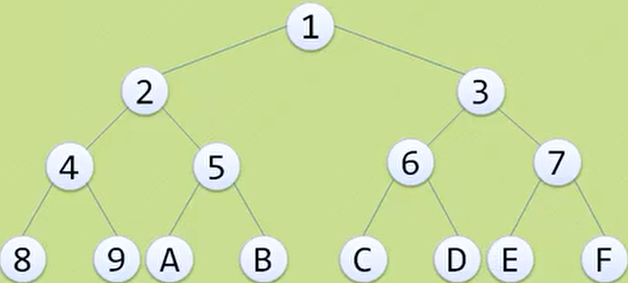
前序遍历:若二又树为空,则空操作返回;否则先访问根结点,然后前序遍历左子树,再前序遍历右子树(遍历次序为:
ABDHIEJCFKG)
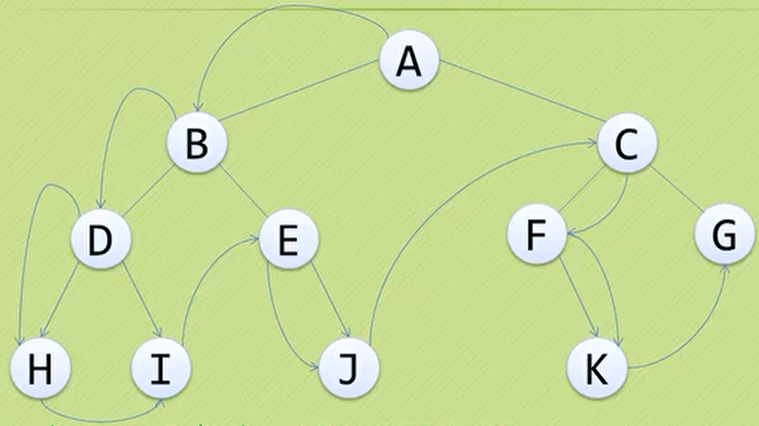
-
中序遍历:若树为空,则空操作返回;否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树(遍历次序为:
HDIBEJAFKCG)
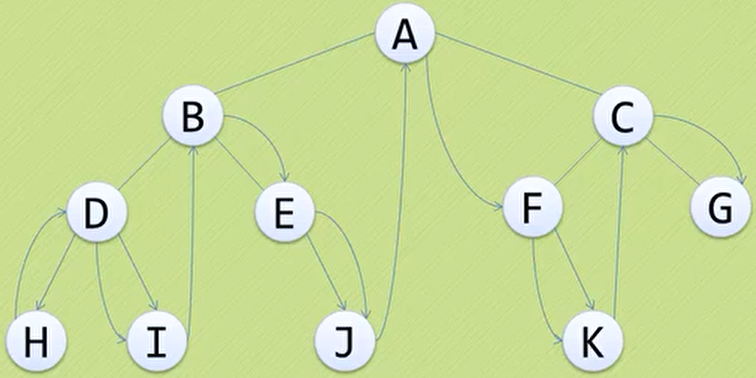
-
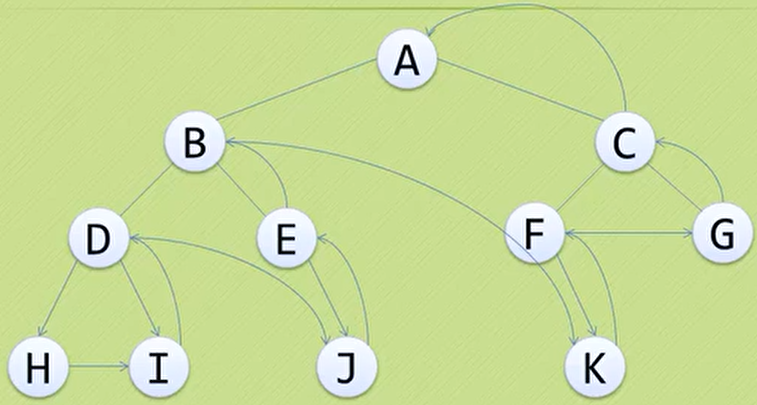
后序遍历:若树为空,则空操作返回;否则从左到右先叶子后结点的方式遍历访问左右子树,最后访问根结点(遍历次序为:
HIDJEBKFGCA)
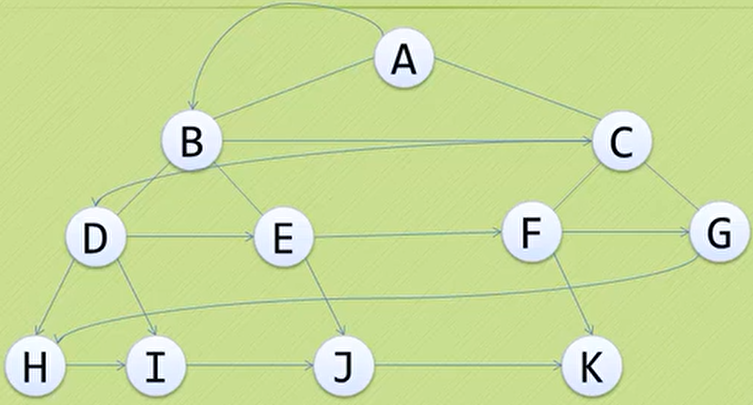
- 层序遍历:若树为空,则空操作返回;否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问(遍历次序为:
ABCDEFGHIJK)![]()
1 #include <stdio.h> 2 #include <stdlib.h> 3 4 typedef int DataType; 5 6 typedef struct Node{ 7 DataType Data; 8 struct Node *lChild, *rChild; 9 }BinTNode, *BiTree; 10 11 void Create_BinTree(BiTree *T) 12 { 13 char ch; 14 scanf("%c",&ch); 15 16 if(ch=='#') *T==NULL; 17 else 18 { 19 *T=(BinTNode*)malloc(sizeof(BinTNode)); 20 (*T)->Data=ch; 21 (*T)->lChild=NULL; 22 (*T)->rChild=NULL; 23 Create_BinTree(&(*T)->lChild);//建立左子树 24 Create_BinTree(&(*T)->rChild);//建立右子树 25 } 26 } 27 28 void DestroyBitTree(BiTree *T)//销毁二叉树 29 { 30 if(*T) 31 { 32 if((*T)->lChild) 33 DestroyBitTree(&(*T)->lChild); 34 if((*T)->rChild) 35 DestroyBitTree(&(*T)->rChild); 36 37 free(*T); 38 *T=NULL; 39 } 40 } 41 42 //遍历二叉树 43 void PreOrder_Traverse(BiTree T)//先序遍历 44 { 45 if(T==NULL) return; 46 else 47 { 48 printf(" %c " , T->Data); 49 PreOrder_Traverse(T->lChild); 50 PreOrder_Traverse(T->rChild); 51 } 52 53 } 54 55 void InOrder_Traverse(BiTree T)//中序遍历 56 { 57 if(T==NULL) return; 58 else 59 { 60 InOrder_Traverse(T->lChild); 61 printf(" %c " , T->Data); 62 InOrder_Traverse(T->rChild); 63 } 64 65 } 66 67 void PostOrder_Traverse(BiTree T)//后序遍历 68 { 69 if(T==NULL) return; 70 else 71 { 72 PostOrder_Traverse(T->lChild); 73 PostOrder_Traverse(T->rChild); 74 printf(" %c " , T->Data); 75 } 76 }


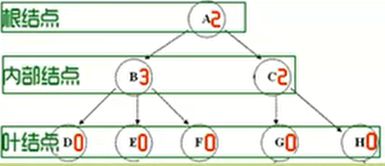


 浙公网安备 33010602011771号
浙公网安备 33010602011771号