自编码器

自编码器

自编码器(Autoencoder)是一种特定的神经网络结构，其目的是为了将输入信息映射到某个更低维度的空间，生成包含重要特征的编码code，这部分称为Encoder，可用函数 \(h=f(x)\) 表示， 然后再利用Decoder将code重构成为尽量能还原原输入的结果，用函数 \(r=g(h)\) 。网络模型目的就是尽量使 \(g(f(x))=x\) ，当然如果只是简单的将输入复制到输出是没有任何意义的，所以需要加一定的限制条件，使模型学习到数据中更重要的特征。有的时候，我们也需要将这种确定 性的函数拓展到具有随机性的概率分布 \(p_{\text {encoder }}(h \mid x)\) 和 \(p_{\text {decoder }}(x \mid h)\) 。

欠完备编码器

为了学习到重要的特征，我们可以限制编码 \(h\) 的维度小于输入，这种编码器成为欠完备编码器 (Undercomplete Autoencoder)。其损失函数可以表示为 \(L(x, g(f(x)))\) ，函数 \(L\) 度量 \(g(f(x))\) 偏离输入 \(x\) 的程度。当decoder函数 \(g\) 是线性函数， \(L\) 是均方差的时候，欠完备编码器学习到的空间与PCA (主成分分析) 相同。对于带有非线性函数编码解码函数的欠完备编码器，即使编码 \(h\) 的维度小于输入，我们也可以任意的改变非线性函数，将输入复制到输出而无需学习到有效的信息，所以怎样限制模型的容量才是关键。

正则自编码器

正则自编码器(Regularized Autoencoder)通过向损失函数中加入对模型复杂度的惩罚项可以有效的解决模型容量过大的问题。模型的训练过程就需要在如下两种冲突中寻找平衡：1. 学习输入数 据 \(x\) 的有效表示 \(h\) ，使得decoder可以有效的通过 \(h\) 重构 \(x\) 。2.满足惩罚项带来的限制条件，这可 以通过限制模型的容量大小，也可以通过改变模型的重构损失，通常会使模型对于输入的扰动更不敏感。以下是三种书本介绍的自编码器。

稀疏自编码器(Sparse Autoencoder)

向损失函数中加入关于编码的稀疏惩罚项 \(\Omega(h)\) ，例如 \(\Omega(h)=\lambda \sum_i\left|h_i\right|\) 。这样学习到的稀疏的表示提取了原数据中更重要的一些特征。

去噪自编码器(Denoising Autoencoder)

简称DAE，其输入是被损坏的数据，结果是希望能够重构未损坏的原数据。其训练过程：

1. 从训练数据中取样样本 \(x\) 。

2. 取样对应的损坏的结果 \(\tilde{x}\) ，这可以用条件概率 \(C(\tilde{x} \mid x=x)\) 来表示。

3. 将 \((x, \tilde{x})\) 作为训练数据来预测重构分布 \(p_{\text {reconstruct }}(x \mid \tilde{x})=p_{\text {decoder }}(x \mid h)\) ，其中 \(h\) 是编码器 \(f(\tilde{x})\) 的输出。

我们可以将DAE训练过 程看做是对于如下的期望的随机梯度下降过程

\[-E_{x \sim \hat{p}_{\text {data }}(x)} E_{\tilde{x} \sim C(\tilde{x} \mid x)} \log p_{\text {decoder }}(x \mid h=f(\tilde{x})) \]

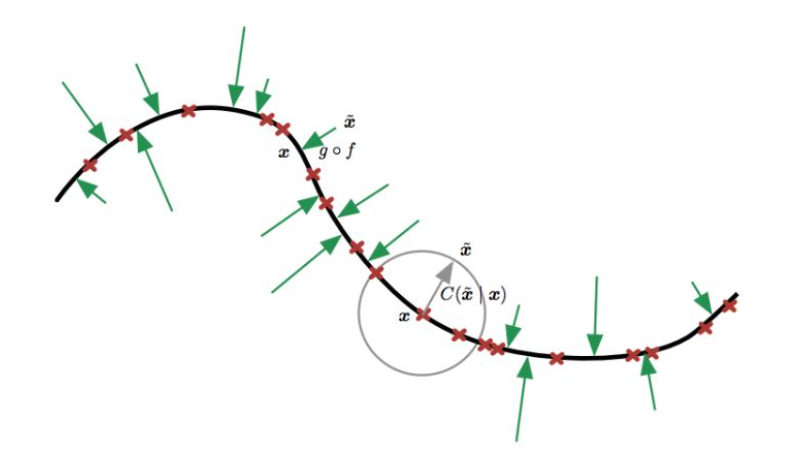
如下图所示我们利用 \(g \circ f\) 操作将受损 数据 \(\tilde{x}\) 尽量映射回原数据 \(x\) 所在的线上，也可以理解为DAE就是令重构函数更能抵抗输入中的微扰。

收缩自编码器(Contractive Autoencoder)

收缩自编码器的惩罚项表示为 \(\Omega(h)=\lambda\left\|\frac{\partial f(x)}{\partial x}\right\|_F^2\) ，是雅可比矩阵的Frobenius范数，可理解为使得encoder更能抵抗输入中的微扰。

去噪自编码器和收缩自编码器之间存在一定联系: 在小高斯噪声的限制下, 当重构函数将 \(\boldsymbol{x}\) 映射到 \(\boldsymbol{r}=g(f(\boldsymbol{x}))\) 时, 去噪重构误差与收缩惩罚项是等价的。换句话说, 去噪自编码器能抵抗小且有限的输人扰动, 而收缩自编码器使特征提取函数能抵抗极小的输人扰动。
分类任务中, 基于 Jacobian 的收缩惩罚预训练特征函数 \(f(x)\), 将收缩惩罚应用在 \(f(x)\) 而不是 \(g(f(x))\) 可以产生最好的分类精度。应用于 \(f(x)\) 的收缩惩罚与得分匹配也有紧密的联系。

收缩 (contractive) 源于 CAE 弯曲空间的方式。具体来说, 由于 CAE 训练为抵抗输人扰动, 鼓励将输入点邻域映射到输出点处更小的邻域。我们能认为这是将输入的邻域收缩到更小的输出邻域。
说得更清楚一点, CAE只在局部收缩一个训练样本，将 \(x\) 的所有扰动都映射到 \(f(x)\) 的附近。全局来看, 两个不同的点 \(x\) 和 \(x^{\prime}\) 会分别被映射到远离原点的两个点 \(f(\boldsymbol{x})\) 和 \(f\left(\boldsymbol{x}^{\prime}\right)\) 。\(f\) 扩展到数据流形的中间或远处是合理的，当 \(\Omega(h)\) 惩罚应用于 sigmoid 单元时, 收缩 Jacobian 的简单方式是令 sigmoid 趋向饱和的 0 或 1 。这鼓励 CAE 使用 sigmoid 的极值编码输入点, 或许可以解释为二进制编码。它也保证了 CAE 可以穿过大部分 sigmoid 隐藏单元能张成的超立方体, 进而扩散其编码值。(?这句话理解不能)
我们可以认为点 \(x\) 处的 Jacobian 矩阵 \(J\) 能将非线性编码器近似为线性算子。这允许我们更形式地使用 “收缩” 这个词。在线性理论中, 当 \(J x\) 的范数对于所有单位 \(x\) 都小于等于 1 时, \(J\) 被称为收缩的。换句话说, 如果 \(J\) 收缩了单位球, 他就是收缩的。我们可以认为 \(\mathrm{CAE}\) 为鼓励每个局部线性算子具有收缩性, 而在每个训练数据点处将 Frobenius 范数作为 \(f(x)\) 的局部线性近似的惩罚。

tips:正则自编码器基于两种相反的推动力学习流形。在 CAE 的情况下, 这两种推动力是重构误差和收缩偍罚 \(\Omega(h)\) 。单独的重构误差鼓励 CAE 学习一个恒等函数。单独的收缩㤠罚将鼓励 CAE 学习关于 \(x\) 是恒定的特征。这两种推动力的的折衷产生导数 \(\frac{\partial f(x)}{\partial x}\) 大多是微小的自编码器。只有少数隐藏单元, 对应于一小部分输人数据的方向, 可能有显著的导数。这其实就是自编码器学习流形的方法。

CAE 的目标是学习数据的流形结构。使 \(J x\) 很大的方向 \(x\), 会快速改变 \(h\), 因 此很可能是近似流形切平面的方向。Rifai的实验显示训练 CAE 会 导致 \(J\) 中大部分奇异值 (幅值) 比 1 小, 因此是收缩的。然而, 有些奇异值仍然比 1 大, 因为重构误差的惩罚鼓励 CAE 对最大局部变化的方向进行编码。对应于最大奇异值的方向被解释为收缩自编码器学到的切方向。理想情况下, 这些切方向应对应于数据的真实变化。比如, 一个应用于图像的 CAE 应该能学到显示图像改变的切向量。

自编码器应用

自编码器的主要应用有降维(dimensionality reduction)和信息检索(information retrieval)。降维前面已经提到，通过encoder我们可以将较复杂的输入编码到维度较低的空间中。信息检索主要是指从数据库中找到与用户的查询条目相近的条目，如果我们利用Autoencoder有效的将每个条目降维并用二进制编码每个维度上的值，则我们可以将数据库中的所有条目产生对应的在低维空间上的哈希码，我们可以有效的提取与用户的查询相同的哈希码，也可以通过改变某几个位上的比特值来寻找与用户相类似的条目，这种方法称为semantic hashing。

小结

自编码器作为降维的优秀工具，是非常重要且泛用性好的工具，值得深入研究掌握。但是书本对其的数学原理讲解一言难尽，因此笔记在此没有过多涉及，以后再进行补足。