线性因子模型

线性因子模型

线性因子

之前总结的方法大部分是在 有大量数据情况下的监督学习方法，而假如我们想减小数据量的要求，则需要一些无监督学习及半监督学习方法，虽然有很多无监督学习方法，但是目前还无法达到深度学习在监督学习问题中所达到的精度，这常常是由于我们需要解决的问题的维度过高或计算量过大造成的。
无监督学习常常需要建立一种依赖于观察数据的概率模型 \(p_{\text {model }}(x)\) ，但由于实际观察的数据 \(x\) 常常比较杂乱没有规律，通常我们会用某种代表了更低维基本特征的隐性变量(latent variables) \(h\) 来更好的表征数据，将问题转化为 \(p_{\text {model }}(x)=E_h p_{\text {model }}(x \mid h)\) ，这一章主要介绍了最基本的 利用隐性变量的概率模型――线性因子模型(Linear Factor model)，即假定 \(h\) 取自某种先验分布 (prior distribution) \(h \sim p(h)\) ，而我们观察到的数据是 \(h\) 的线性变换与一些随机噪声的叠加， 用式子表示为

\[x=W h+b+ noise \]

之后讨论的不同方法会选择不同的 \(p(h)\) 和\(noise\)分布。

因子分析(Factor Analysis)模型中，\(h\) 满足单位高斯分布

\[h \sim N(h ; 0, I), \]

而观察数据 \(x\) 相对于 \(h\) 则相互条件独立，noise来自于对角协方差高斯分布，其协方差矩阵 \(\psi=\operatorname{diag}\left(\sigma^2\right)\) ，其中 \(\sigma^2=\left[\sigma_1^2, \sigma_2^2, \ldots, \sigma_n^2\right]^T\) 是每个变量的协方差。

常见的因子分析模型

概率主成分分析(Probabilistic PCA)模型与因子分析模型类似，但是我们令所有的协方差 \(\sigma_i^2\) 都相等，即

\[x=W h+b+\sigma z \]

其中

\[z \sim N(z ; 0, I) \]

是单位高斯噪声。若 \(\sigma \rightarrow 0\) 时，PPCA收敛至PCA。

独立成分分析(Independent Component Analysis)简称ICA，希望隐性变量尽量互相独立，变成原本每个人的语音。另外，ICA 并不一定需要生成模型即知道怎样模拟 \(h\) 的生成概率分布 \(p(h)\) ，许多ICA的变种只是将目标定为尽量提高 \(h=W^{-1} x\) 的峰度以尽可能偏离高斯分布，而无需明确的表示 \(h\) 的生成概率分布 \(p(h)\)。

慢特征分析(Slow Feature Analysis)简称SFA，希望学习随时间变化较为缓慢的特征，其核心思想是认为一些重要的特征通常相对于时间来讲相对变化较慢，例如视频图像识别中，假如我们要探 测图片中是否包含斑马，两帧之间单个像素可能从黑突变为白，所以我们需要一些随时间变化更慢 的特征来决定我们的预测结果。假设我们的特征提取函数为 \(f\) ，则慢特征原则希望减小如下的损失函数

\[\lambda \sum_t L\left(f\left(x^{(t+1)}\right), f\left(x^{(t)}\right)\right) \]

SFA即假定特征提取函数 \(f(x ; \theta)\) 为线性变换，进而解决如下的优化问题

\[\min _\theta E_t\left(f\left(x^{(t+1)}\right)_i-f\left(x^{(t)}\right)_i\right)^2 \]

并要求限制条件 \(E_t\left(f\left(x^{(t)}\right)_i\right)=0\) 及 \(E_t\left[f\left(x^{(t)}\right)_i^2\right]=1\) 以保证解的唯一性。
另外我们还要求各个不同特征之间是去相关的 \(\forall i<j, E_t\left[f\left(x^{(t)}\right)_i f\left(x^{(t)}\right)_j\right]=0\) ，否则所有的特征都会变成最慢的那个信号的不同表征。

稀疏编码(Sparse Coding)希望隐性特征更稀疏，即集中在少数几个特征上，所以它的先验函数通常选为在零点附近有比较陡峭的峰值的函数，例如拉普拉斯函数

\[p\left(h_i\right)=\operatorname{Laplace}\left(h_i ; 0, \frac{2}{\lambda}\right)=\frac{\lambda}{4} e^{-\frac{1}{2} \lambda\left|h_i\right|} \]

由于我们定义了

\[p(x \mid h)=N\left(x ; W h+b, \frac{1}{\beta} I\right) \]

优化问题就变成了 \(p(x|h)\) 的最大似然估计，也就是 \(\operatorname{argmin}_h \lambda\|h\|_1+\beta\|x-W h\|_2^2\) 。这里的稀疏约束是通过拉普拉斯概率函数的先验加入的，这在第四章中有介绍。

由于在 \(h\) 上施加 \(L^1\) 范数, 这个过程将产生稀疏的 \(h^*\) 。为了训练模型而不仅仅是进行推断, 我们交替迭代关于 \(h\) 和 \(W\) 的最小化过程。在本文中, 我们将 \(\beta\) 视为超参数。我们通常将其设置为 1 , 因为它在此优化问题的作用与 \(\lambda\) 类似, 没有必要使用两个超参数。原则上, 我们还可以将 \(\beta\) 作为模型的参数, 并学习它。我们在这里已经放弃了一些不依赖于 \(h\) 但依赖于 \(\beta\) 的项。要学习 \(\beta\), 必须包含这些项，否则 \(\beta\) 将退化为 0 。

不是所有的稀疏编码方法都显式地构建了一个 \(p(\boldsymbol{h})\) 和一个 \(p(\boldsymbol{x} \mid \boldsymbol{h})\) 。通常我们只是对学习一个带有激活值的特征的字典感兴趣, 当特征是由这个推断过程提取时, 这个激活值通常为 0 。

PCA流形解释

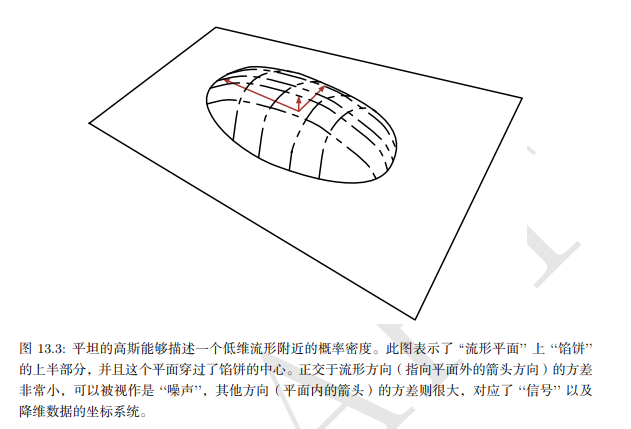
线性因子模型, 包括 PCA 和因子分析, 可以理解为学习一个流形。CA 定义为高概率的薄饼状区域, 即一个高斯分布, 沿着 某些轴非常窄, 就像薄饼沿着其垂直轴非常平坦, 但沿着其他轴是细长的, 正如薄饼在其水平轴方向是很宽的一样。4PCA 可以理解为将该薄饼与更高维空间中的线性流形对准。这种解释不仅适用于传统PCA, 而且适用于学 习矩阵 \(W\) 和 \(V\) 的任何线性自编码器, 其目的是使重构的 \(x\) 尽可能接近于原始的 \(x_0\) 。

编码器表示为

\[h=f(\boldsymbol{x})=\boldsymbol{W}^{\top}(\boldsymbol{x}-\boldsymbol{\mu}) . \]

编码器计算 \(h\) 的低维表示。从自编码器的角度来看, 解码器负责计算重构:

\[\hat{\boldsymbol{x}}=g(\boldsymbol{h})=\boldsymbol{b}+\boldsymbol{V} \boldsymbol{h} \]

能够最小化重构误差

\[\mathbb{E}\left[\|x-\hat{x}\|^2\right] \]

的线性编码器和解码器的选择对应着 \(V=W, \mu=b=\mathbb{E}[x], W\) 的列形成一组标准正交基，这组基生成的子空间与协方差矩阵 \(C\)

\[C=\mathbb{E}\left[(\boldsymbol{x}-\boldsymbol{\mu})(\boldsymbol{x}-\boldsymbol{\mu})^{\top}\right] \]

的主特征向量所生成的子空间相同。在 PCA 中, \(W\) 的列是按照对应特征值（其全部是实数和非负数) 幅度大小排序所对应的特征向量。
我们还可以发现 \(C\) 的特征值 \(\lambda_i\) 对应了 \(x\) 在特征向量 \(v^{(i)}\) 方向上的方差。如果 \(\boldsymbol{x} \in \mathbb{R}^D, h \in \mathbb{R}^d\) 并且满足 \(d<D\), 则 (给定上述的 \(\boldsymbol{\mu}, \boldsymbol{b}, \boldsymbol{V}, \boldsymbol{W}\) 的情况下) 最佳的重 构误差是

\[\min \mathbb{E}\left[\|\boldsymbol{x}-\hat{\boldsymbol{x}}\|^2\right]=\sum_{i=d+1}^D \lambda_i . \]

因此, 如果协方差矩阵的秩为 \(d\), 则特征值 \(\lambda_{d+1}\) 到 \(\lambda_D\) 都为 0 , 并且重构误差为 0。 此外, 我们还可以证明上述解可以通过在给定正交矩阵 \(W\) 的情况下最大化 \(h\) 元素的方差而不是最小化重构误差来获得。

小结

因子分析，概率PCA，ICA，SFA即稀疏编码等线性因子模型是比较简单的学习数据的高效表征的方法，而且它们也可以扩展为之后更复杂的自编码网络以及深度概率模型，所以有必要对其有基本的理解。