正则化

正则化

总体来说，一部分正则化方法使给模型施加额外的限制条件，例如限制参数值范围，有些会在目标函数中添加一些额外惩罚项，本质上也是希望限制参数值。有的时候，这些限制条件或惩罚项代表了特定的先验经验，有的时候是希望避免模型过于复杂。正则化常常会增加一些bias但同时会减少variance，好的正则化方法就是在能够显著减小variance的情况下又不显著地增加bias。

解释一下为什么会增加bias，极大似然估计的渐进估计性质告诉我们，当样本量趋于无限大时，极大似然估计趋近于无偏估计，这是MLE特有的性质。但是当优化目标不再是似然函数时，此时求出的统计量就不一定是MLE了，通常来说这时的参数是一个有偏估计，但是其在增加了正则化项的批判准则下是最佳估计量。

下面来总结一下常见的几种正则化方法:

Parameter Norm Penalties

即在目标函数中添加对于参数的惩罚项以减小模型的capacity，即:

\[\tilde{J}(\theta ; X, y)=J(\theta ; X, y)+\alpha \Omega(\theta) \]

其中 \(\alpha \in[0, \infty)\) 是一个标志着惩罚项权重的超参数。当 \(\alpha\) 为零时，正则项为零， \(\alpha\) 越大，则正则化越显著。由于加入了关于参数大小的惩罚项，模型训练过程不仅仅是要减小训练集上的目标函数，而且也要保持惩罚项尽量小，常见的惩罚项有 \(L^2\) regularization和 \(L^1\) regularization。其中 \(L^2\) regularization是减小权重的大小，而 \(L^1\) regularization会使权重更稀硫，具体分析如下:

\(L^2\) regularization也被称作weight decay(权重衰减)，通过增加 \(\Omega(\theta)=\frac{1}{2}\|w\|_2^2\) 的正则项， 可以使权重大小减小。
为什么 \(L^2\) 可以减小权重w的大小呢? 我们可以先从每次梯度下降更新的大小来理解:

对于 \(\tilde{J}(w ; X, y)=J(w ; X, y)+\frac{\alpha}{2} w^T w\) ，其梯度为 \(\nabla_w \tilde{J}(w ; X, y)=\nabla_w J(w ; X, y)+\alpha w\) ，则每次更新法则为

\[w \leftarrow(1-\epsilon \alpha) w-\epsilon \nabla_w J(w ; X, y) \]

可以看出， \(L^2\) 的引入使得每次步进时权重有一个常数衰减。对于单次步进如此，那么最终的w结果呢?
我们可以将目标函数在使原目标函数最小的 \(w^*=\operatorname{argmin}_w J(w)\) 附近进行二次展开 \(\tilde{J}(w)=J\left(w^*\right)+\alpha w+\frac{1}{2}\left(w-w^*\right)^T H\left(w-w^*\right)\) ，其中H为Hessian matrix。该函数的极小值应取在满足 \(\nabla_w \tilde{J}(w)=\alpha w+H\left(w-w^*\right)=0\) 的 \(w\) ，用 \(\tilde{w}\) 代表新的极值点, 则

\[\tilde{w}=(H+\alpha I)^{-1} H w^* \]

可以看出当 \(\alpha\) 接近零时， \(\tilde{w}\) 趋近于 \(w^*\) ，而对于 \(\alpha\) 远离零的情况，我们可对 \(H\) 作特征分解为 \(H=Q \Lambda Q^T\) ，则

\[\tilde{w}=Q(\Lambda+\alpha I)^{-1} \Lambda Q^T w^* \]

可以看出 \(\tilde{w}\) 相对于 \(w^*\) 是沿着 \(H\) 的特征向量的轴线进行了尺度收缩，即沿着 \(i\) 特征向量的方向收缩了 \(\frac{\lambda_i}{\lambda_i+\alpha}\) ，对于特征值较大的 \(\lambda_i \gg \alpha\) 的方向，正则项作用很小，而对于 \(\lambda_i \ll \alpha\) 的方 向，正则项作用显著， \(\tilde{w}_i\) 趋向于零，如下图中所示

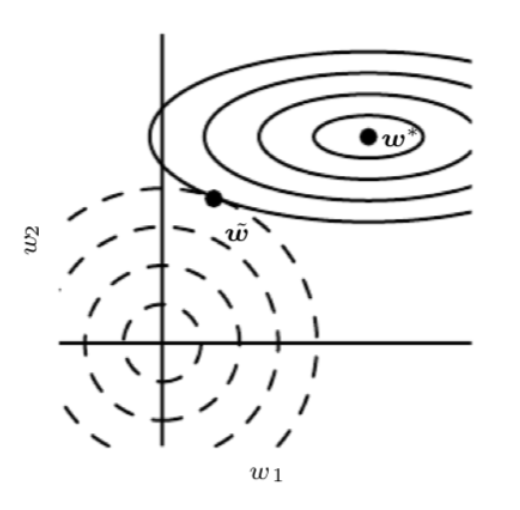
图中实心线为不含正则项的原目标函数的等高线，虚线为正则项的等高线， \(\tilde{w}\) 为新的目标函数的极值点。对于 \(w_1\) 方向，Hessian matrix的本征值很小，原目标函数对于这一水平方向的移动不敏感，所以正则项可沿 \(w_1\) 方向从原极值点 \(w^*\) 作出较大横移，使其趋于零，而对于 \(w_2\) 方向，其曲 率较大，本征值较大，目标函数对于这一方向的移动非常敏感，导致正则项不能很大的改变 \(w_2\) 方 向上的值。

\(L^1\) regularization则是加入了对于每一个元素的绝对值的求和惩罚项 \(\Omega(\theta)=\|w\|_1=\sum_i\left|w_i\right|\) ，新的目标函数为 \(\tilde{J}(w ; X, y)=J(w ; X, y)+\alpha\|w\|_1\) ，其梯度为 \(\nabla_w \tilde{J}(w ; X, y)=\nabla_w J(w ; X, y)+\alpha \operatorname{sign}(w)\), 其中sign为正负号函数。
类似于 \(L^2\) regularization的处理过程，我们同样可以对新的目标函数进行二次展开，为方便讨论，假设Hessian matrix是对角矩阵，则新的目标函数可近似为 \(\tilde{J}(w)=J\left(w^*\right)+\sum_i\left[\frac{1}{2} H_{i, i}\left(w_i-w_i^*\right)^2+\alpha\left|w_i\right|\right]\) ，其极值满足

\[\tilde{w}_i=\operatorname{sign}\left(w_i^*\right) \max \left\{\left|w_i^*\right|-\frac{\alpha}{H_{i, i}}, 0\right\} \]

我们考虑 \(w_i^*>0\) 的情况， \(w_i^*<0\) 可做类似分析，

1. \(w_i^* \leq \frac{\alpha}{H_{i, i}}\) ，则极值点为 \(\tilde{w}_i=0\)

2. \(w_i^*>\frac{\alpha}{H_{i, i}}\) ，则 \(\tilde{w}_i=w_i^*-\frac{\alpha}{H_{i, i}}\) 不为零，而仅仅移动了 \(\frac{\alpha}{H_{i, i}}\) 的距离。

与 \(L^2\) regularization相对比， \(L^1\) regularization使权重更稀疏(sparse)，即使很多项最优值为零，而 对应的 \(L^2\) 仅是使权重更小而不为零。\(L^1\) regularization由于其稀疏化的性质常常被用来做特征选择(feature selection)，因为它可以使 某些权重为零，说明相对应的特征可以安全地忽略掉，经典的LASSO(least absolute shrinkage and selection operator)就是利用了 \(L^1\) penalty。

Regularization and Underconstrained Problems

在有些情况下我们会遇到欠定的机器学习问题，例如线性回归中我们需要对 \(X^{T}X\) 求逆以得到闭解，但是在大部分情况下该矩阵是奇异的。此时引入正则化可以让我们保证该矩阵可逆，例如求解 \(X^TX+\alpha I\) 的逆。这种操作可以理解为将无限的解通过正则化约束将解的数量减小到一个，此时我们就可以获得闭解。思考Moore-Penrose伪逆 \(X^+\) 的数学定义

\[X^+ = \lim_{\alpha \rightarrow 0}(X^TX+\alpha I)^{-1}X^T \]

伪逆其实就是使用正则化约束来稳定欠定的一种方法。

Dataset Augmentation

使机器学习模型效果更好的很自然的一种办法就是给它提供更多的训练数据，当然实际操作中，有时候训练集是有限的，我们可以制造一些假数据并添加入训练集中，当然这仅对某些机器学习问题适用，例如对于图像识别，我们可以平移图像，添加噪声，旋转，色调偏移等等，我们希望模型能够在这些变换或干扰不受影响保持预则的准确性，从而减小泛化误差。当然，我们要注意这些变换 不能改变数据的原始标记，如对于识别数字问题，我们就不能对6和9进行180度旋转。

Multi-task learning

与Dataset augmentation类似，多任务学习也是希望令模型的参数能够进行很好的泛化，其原理是对多个目标共享模型的一部分 (输入及某些中间的表示层)，使其对于多个有关联的目标均有较好的效果，保证模型可以更好的推广。

tips：参数共享带有很强的先验知识(我认定你们学到的东西大差不差！)，只对符合模型的任务有好的效果，且在关联任务上泛化能力强。

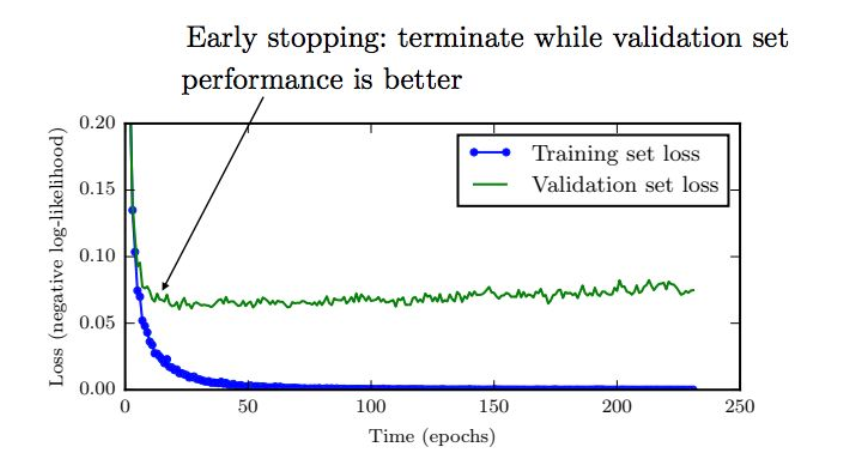
Early stopping

通常对于较大的模型，我们会观察到训练集上的误差不断减小，但验证集上的误差会在某个点之后反而逐渐增大，这意味着为了减小泛化误差，我们可以在训伡过程中不断的记录验证集上的误差及对应的模型参数，最终返回验证集上误差最小所对应的模型参数，这个简单直观的方法就是early stopping，由于其简单高效，在深度学习中得到了广泛应用。其效果和L2正则化类似，由于停止较早，解会靠近原点。

Sparse Representations

\(L^1\) regularization是使参数更稀疏，同样的我们也可以通过增加对于表征层的norm penalty项使表征 (隐藏层) 更稀疏。即 \(\tilde{J}(\theta ; X, y)=J(\theta ; X, y)+\alpha \Omega(h)\)

Bagging and Ensemble

Bagging(全称是bootstrap aggregating)通过整合多个模型来减小泛化误差，其基本思想是多个模型对于训练集做出同样错误预测的概率较小，Bagging是ensemble methods (集成算法) 的一种方法。
例如假设我们有 \(\mathrm{k}\) 个回归模型的集合，对于一个数据，每个模型的误差是 \(\epsilon_i\) ，假设误差满足多元正态分布且方差 \(E\left[\epsilon_i^2\right]=v\) ，协方差 \(E\left[\epsilon_i \epsilon_j\right]=c\) ，则ensemble之后的误差平方的期望为

\[E\left[\left(\frac{1}{k} \sum_i \epsilon_i\right)^2\right]=\frac{1}{k^2} E\left[\left(\sum_i \epsilon_i^2+\sum_{j \neq i} \epsilon_i \epsilon_j\right)\right]=\frac{1}{k} v+\frac{k-1}{k} c \]

当误差间完全相关时，则 \(c=v\) ，均方差仍为 \(v\) ，ensemble并没有达到更好效果，但如果误差 间完全不相关，则 \(c=0\) ，则均方差缩小至 \(\frac{1}{k} v\), 说明均方差随ensemble的集合大小而线性减 小，实际应用中，介于这两种情况之间，通常ensemble效果会远好于其中单一模型的效果。
ensemble方法可以是将完全不同的模型结合起来，而Bagging方法则是同一种模型和目标函数， 但是产生k种不同的训练集，每个训练集与原训练集所含数据量相同，但会以某一概率去掉某些样 本并以其他的重复样本代替，第i个模型就在第 \(\mathrm{i}\) 个训䌸集上进行训练。例如下图中所示，我们想鉴 别某个数字是否是 8 ，原数据包含 \(9 ， 6\) 和8，第一个重新取样的数据集中仅包含 6 和 8 ，9倍替换掉， 则模型1会学习到需要数字有上半圈才能为 8 ，而第二个重新取样的数据集中去掉 6 ，仅包含 9 和 8 ， 则模型2会学习到数字需有下半圈才能为 8 ，将他们集合起来就可以比较准确的推测需要同时有上下半圈才鉴定数字为 8 。

Dropout

Dropout可以理解做是将ensemble应用到大型神经网络的一种更为实际有效的方法。由于 ensemble需要训练多个模型，对于大型神经网络，其训练和评估所需时间和存储资源较大，这种 方法常常不太实际，Dropout就提供了一个更便宜的解决方案：即通过随机去掉一些节点的方法训练多个子网络，并最终将这些子网络ensemble起来，如下图所示:

其具体方法是当我们利用minibatch的算法如随机梯度下降算法来学习时，我们可以随机的选取一个binary mask(0表示节点输出为零，1表示正常输出该节点) 决定哪些输入和隐藏层节点保留， 每次的mask的选择是独立的。而mask为1的概率是我们可以调控的超参数。
和bagging方法相比，bagging中每个模型是完全独立的，而dropout中，模型间由于继承了父网络中的参数的子集会共享一些参数，这使得在有限的存储空间中我们可以表示多个模型。
以上是训练过程，而在做inference预测时，我们需要取所有模型的预测的均值，但是这往往计算量过多，Hinton提出inference时我们实际可以只用一个模型但其中每个节点的权重需要乘以包含这个节点的概率，这种方法称作weight scaling inference rule。实际中，我们常常把weight scaling过程放在训练过程中，即训练中每个节点输出就乘以包含该节点的概率的倒数，则inference时只需要正常的通过一遍前馈过程即可，不需要在进行weight scaling。
Dropout的优势在于其计算资源占用小，并且对于模型或训练算法的限制较小，基本上可以适用于各种前馈网络，循环网络或概率模型，所以实际工业模型中应用很多。

Adversarial Training

Adversarial Training对抗训练很有意思，它让人们深入思考机器学习究竟学到了什么有效信息。 这方面的工作主要是由谷歌的Szegedy和本书作者lan Goodfellow进行的。他们可以制造一些对抗样本迷惑神经网络，如下图中所示，他们对于熊猫图片加了一些人眼不可见的干扰，形成新样本，而新的人眼仍可鉴定为熊猫的图片却会被机器以较大置信率鉴定为长臂猿。为什么在人类看来类似的样本机器会得到大相径庭的结论呢? Ian认为这是由于神经网络中的大部分组成还是线性的(如ReLU可以看成是分段线性)，而对于不同的输入，线性函数会受到较大的扰动，产生较大的改变。为了解决这一问题，他们会将这些对抗样本重新加到训练集中，使得神经网络倾向于对于数据集保持局部稳定而不至干扰过大，从而学习到更有效的信息。