二叉树的四种遍历方法笔记 c实现树（二叉树）的建立和遍历算法（一）（前序，中序，后序）

c实现树（二叉树）的建立和遍历算法（一）（前序，中序，后序）

最近学习树的概念，有关二叉树的实现算法记录下来。。。

不过学习之前要了解的预备知识：树的概念；二叉树的存储结构；二叉树的遍历方法。。

二叉树的存储结构主要了解二叉链表结构，也就是一个数据域，两个指针域，（分别为指向左右孩子的指针），从下面程序1，二叉树的存储结构可以看出。

二叉树的遍历方法：主要有前序遍历，中序遍历，后序遍历，层序遍历。（层序遍历下一篇再讲，本篇主要讲的递归法）

下篇主要是非递归遍历，之后会有c++模板实现二叉树和二叉搜索树（用于动态查找）。

如这样一个二叉树：

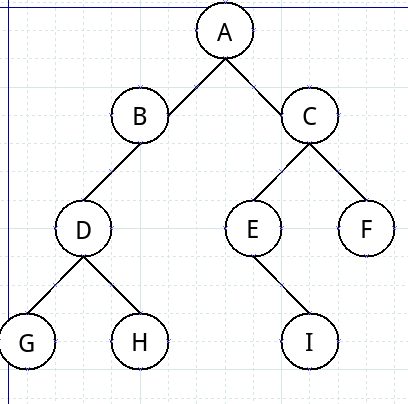
它的前序遍历顺序为：ABDGHCEIF（规则是先是根结点，再前序遍历左子树，再前序遍历右子树）

它的中序遍历顺序为：GDHBAEICF（规则是先中序遍历左子树，再是根结点，再是中序遍历右子树）

它的后序遍历顺序为：GHDBIEFCA（规则是先后序遍历左子树，再是后序遍历右子树，再是根结点）

如果不懂的话，可以参看有关数据结构的书籍。。

1，二叉树的存储结构（二叉链表）

//二叉树的二叉链表结构，也就是二叉树的存储结构，1个数据域，2个指针域（分别指向左右孩子）

typedef  struct BiTNode
{
    ElemType data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

2，首先要建立一个二叉树，建立二叉树必须要了解二叉树的遍历方法。

//二叉树的建立，按前序遍历的方式建立二叉树，当然也可以以中序或后序的方式建立二叉树
void CreateBiTree(BiTree *T)
{
    ElemType ch;
    cin >> ch;
    if (ch == '#')
        *T = NULL;  //保证是叶结点
    else
    {
        *T = (BiTree)malloc(sizeof(BiTNode));
        //if (!*T)
            //exit(OVERFLOW); //内存分配失败则退出。
        (*T)->data = ch;//生成结点
        CreateBiTree(&(*T)->lchild);//构造左子树
        CreateBiTree(&(*T)->rchild);//构造右子树    
    }
}

3.二叉树的遍历（递归方式，非递归方式见下篇：树（二叉树）的建立和遍历算法（二））：

主要有三种方法：

/递归方式前序遍历二叉树
void PreOrderTraverse(BiTree T, int level)
{
    if (T == NULL)
        return;

/*此处表示对遍历的树结点进行的操作，根据你自己的要求进行操作，这里只是输出了结点的数据*/
    //operation1(T->data);
    operation2(T->data, level); //输出了层数

    PreOrderTraverse(T->lchild, level + 1);
    PreOrderTraverse(T->rchild, level + 1);
}

//递归方式中序遍历二叉树

void InOrderTraverse(BiTree T,int level)
{
if(T==NULL)
return;
InOrderTraverse(T->lchild,level+1);

//operation1(T->data);
operation2(T->data, level); //输出了层数

InOrderTraverse(T->rchild,level+1);
}

//递归方式后序遍历二叉树

void PostOrderTraverse(BiTree T,int level)
{
if(T==NULL)
return;
PostOrderTraverse(T->lchild,level+1);
PostOrderTraverse(T->rchild,level+1);

//operation1(T->data);
operation2(T->data, level); //输出了层数
}

4.完整代码：

#include<iostream>
#include<stdlib.h>
using namespace std;

typedef char ElemType;

//二叉树的二叉链表结构，也就是二叉树的存储结构，1个数据域，2个指针域（分别指向左右孩子）

typedef  struct BiTNode
{
    ElemType data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

//二叉树的建立，按前序遍历的方式建立二叉树，当然也可以以中序或后序的方式建立二叉树
void CreateBiTree(BiTree *T)
{
    ElemType ch;
    cin >> ch;
    if (ch == '#')
        *T = NULL;  //保证是叶结点
    else
    {
        *T = (BiTree)malloc(sizeof(BiTNode));
        //if (!*T)
            //exit(OVERFLOW); //内存分配失败则退出。
        (*T)->data = ch;//生成结点
        CreateBiTree(&(*T)->lchild);//构造左子树
        CreateBiTree(&(*T)->rchild);//构造右子树    
    }
}
//表示对遍历到的结点数据进行的处理操作,此处操作是将树结点前序遍历输出
void operation1(ElemType ch)
{
    cout << ch << " ";
}
//此处在输出的基础上，并输出层数
void operation2(ElemType ch, int level)
{
       cout << ch << "在第" << level << "层" << endl;
}


//递归方式前序遍历二叉树
void PreOrderTraverse(BiTree T, int level)
{
    if (T == NULL)
        return;
/*此处表示对遍历的树结点进行的操作，根据你自己的要求进行操作，这里只是输出了结点的数据*/
    //operation1(T->data);
    operation2(T->data, level); //输出了层数

    PreOrderTraverse(T->lchild, level + 1);
    PreOrderTraverse(T->rchild, level + 1);
}

//递归方式中序遍历二叉树

void InOrderTraverse(BiTree T,int level)
{
if(T==NULL)
return;
InOrderTraverse(T->lchild,level+1);

//operation1(T->data);
operation2(T->data, level); //输出了层数

InOrderTraverse(T->rchild,level+1);
}

//递归方式后序遍历二叉树

void PostOrderTraverse(BiTree T,int level)
{
if(T==NULL)
return;
PostOrderTraverse(T->lchild,level+1);
PostOrderTraverse(T->rchild,level+1);

//operation1(T->data);
operation2(T->data, level); //输出了层数
}


int main()
{
    int level = 1; //表示层数
    BiTree T = NULL;
    cout << "请以前序遍历的方式输入扩展二叉树："; //类似输入AB#D##C##
    CreateBiTree(&T);// 建立二叉树，没有树，怎么遍历

    cout << "递归前序遍历输出为：" << endl;
    PreOrderTraverse(T, level);//进行前序遍历，其中operation1()和operation2()函数表示对遍历的结点数据进行的处理操作
    cout << endl;

    cout << "递归中序遍历输出为：" << endl;
    InOrderTraverse(T, level);
    cout << endl;

    cout << "递归后序遍历输出为：" << endl;
    PostOrderTraverse(T, level);
    cout << endl;

    return 0;
}

注意：这里有几个知识点补充下：

（1）建立二叉树时，这里是以前序遍历的方式，输入的是扩展二叉树，也就是要告诉计算机什么是叶结点，否则将一直递归，当输入“#”时，指针指向NULL，说明是叶结点。

如图为扩展二叉树：（前序遍历为：ABDG##H###CE#I##F##）

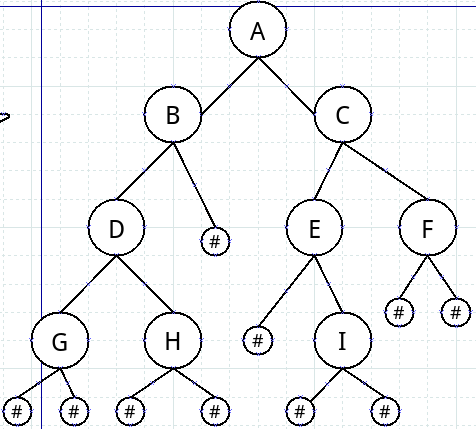
（2）operation1( )函数只是对各个结点的输出；

operation2( )函数不仅输出了各个结点，同时输出了结点所在的层数。（调试时可以只先运行一个）

5.运行结果

只是运行了operation2( )函数，有层数输出：

或者运行只运行operation1( )函数

二叉树的四种遍历方法笔记

二叉树的遍历（traversing binary tree）是指从根结点出发，按照某种次序依次访问二叉树中所有的结点，使得每个结点被访问依次且仅被访问一次。

前序	中	左	右
中序	左	中	右
后序	左	右	中

st=>start: 开始
e=>end: 结束
op=>operation: 根结点
op2=>operation: 左子树

io=>inputoutput: 右子树
cond=>condition: 二叉树是否为空？

st->cond
cond(yes)->e
cond(no)->e
op->op2->io->e

前序遍历

若树为空，则空操作返回。否则，先访问根节点，然后前序遍历左子树，再前序遍历右子树。（W）型（中左右）

中序遍历

若树为空，则空操作返回。否则，从根节点开始（注意并不是先访问根节点），中序遍历根节点的左子树，然后是访问根节点，最后中序遍历根节点的右子树。（M）型，（左中右）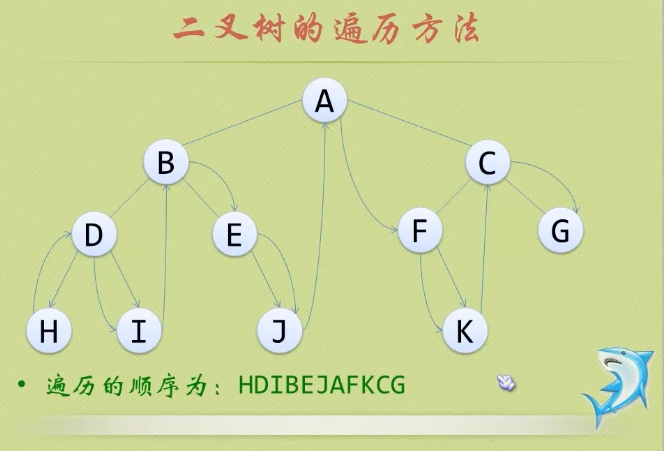

后续遍历

若树为空，则空操作返回。否则，从左到右先叶子后节点的方式遍历访问左右子树，最后访问根节点。（左右中）逆时针型（左右中）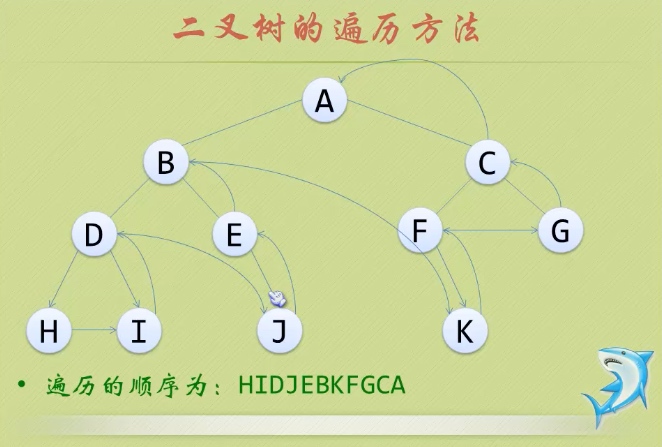

层序遍历

若树为空，则空操作返回。否则，从树的第一层，也就是根节点开始访问，从上到下逐层遍历，在同一层中，按从左到右的顺序结点逐个访问。

#include<iostream>
#include<stdlib.h>
using namespace std;

typedef char ElemType;

//二叉树的二叉链表结构，也就是二叉树的存储结构，1个数据域，2个指针域（分别指向左右孩子）

typedef  struct BiTNode
{
    ElemType data;
    struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;

//二叉树的建立，按前序遍历的方式建立二叉树，当然也可以以中序或后序的方式建立二叉树
void CreateBiTree(BiTree *T)
{
    //ElemType ch;
    //cin >> ch;
    //if (ch == '#')
    //    *T = NULL;  //保证是叶结点
    //else
    //{
    //    *T = (BiTree)malloc(sizeof(BiTNode));
    //    //if (!*T)
    //    //exit(OVERFLOW); //内存分配失败则退出。
    //    (*T)->data = ch;//生成结点
    //    CreateBiTree(&(*T)->lchild);//构造左子树
    //    CreateBiTree(&(*T)->rchild);//构造右子树    
    //}

    *T = (BiTree)malloc(sizeof(BiTNode));
    (*T)->data='A';
    (*T)->lchild=(BiTree)malloc(sizeof(BiTNode));
    (*T)->lchild->data='B';
    (*T)->lchild->lchild=(BiTree)malloc(sizeof(BiTNode));
    (*T)->lchild->lchild->data='D';
    (*T)->lchild->lchild->lchild=(BiTree)malloc(sizeof(BiTNode));
    (*T)->lchild->lchild->lchild->data='H';
    (*T)->lchild->lchild->lchild->lchild=NULL;
    (*T)->lchild->lchild->lchild->rchild=NULL;
    (*T)->lchild->lchild->rchild=(BiTree)malloc(sizeof(BiTNode));
    (*T)->lchild->lchild->rchild->data='I';
    (*T)->lchild->lchild->rchild->lchild=NULL;
    (*T)->lchild->lchild->rchild->rchild=NULL;
    (*T)->lchild->rchild=(BiTree)malloc(sizeof(BiTNode));
    (*T)->lchild->rchild->data='E';
    (*T)->lchild->rchild->lchild=NULL;
    (*T)->lchild->rchild->rchild=(BiTree)malloc(sizeof(BiTNode));
    (*T)->lchild->rchild->rchild->data='J';
    (*T)->lchild->rchild->rchild->lchild=NULL;
    (*T)->lchild->rchild->rchild->rchild=NULL;

    (*T)->rchild=(BiTree)malloc(sizeof(BiTNode));
    (*T)->rchild->data='C';
    (*T)->rchild->lchild=(BiTree)malloc(sizeof(BiTNode));
    (*T)->rchild->lchild->data='F';
    (*T)->rchild->lchild->lchild=NULL;
    (*T)->rchild->lchild->rchild=(BiTree)malloc(sizeof(BiTNode));
    (*T)->rchild->lchild->rchild->data='K';
    (*T)->rchild->lchild->rchild->lchild=NULL;
    (*T)->rchild->lchild->rchild->rchild=NULL;

    (*T)->rchild->rchild=(BiTree)malloc(sizeof(BiTNode));
    (*T)->rchild->rchild->data='G';
    (*T)->rchild->rchild->lchild=NULL;
    (*T)->rchild->rchild->rchild=NULL;
}


//表示对遍历到的结点数据进行的处理操作,此处操作是将树结点前序遍历输出
void operation1(ElemType ch)
{
    cout << ch << " ";
}


//此处在输出的基础上，并输出层数
void operation2(ElemType ch, int level)
{
    cout << ch << "在第" << level << "层" << endl;
}


//递归方式前序遍历二叉树
void PreOrderTraverse(BiTree T, int level)
{
    if (T == NULL)
        return;
    /*此处表示对遍历的树结点进行的操作，根据你自己的要求进行操作，这里只是输出了结点的数据*/
    //operation1(T->data);
    operation2(T->data, level); //输出了层数

    PreOrderTraverse(T->lchild, level + 1);
    PreOrderTraverse(T->rchild, level + 1);
}

//递归方式中序遍历二叉树

void InOrderTraverse(BiTree T,int level)
{
    if(T==NULL)
        return;
    InOrderTraverse(T->lchild,level+1);

    //operation1(T->data);
    operation2(T->data, level); //输出了层数

    InOrderTraverse(T->rchild,level+1);
}

//递归方式后序遍历二叉树
void PostOrderTraverse(BiTree T,int level)
{
    if(T==NULL)
        return;
    PostOrderTraverse(T->lchild,level+1);
    PostOrderTraverse(T->rchild,level+1);

    //operation1(T->data);
    operation2(T->data, level); //输出了层数
}


int main()
{
    int level = 1; //表示层数
    BiTree T = NULL;
    cout << "请以前序遍历的方式输入扩展二叉树：" << endl; //类似输入AB#D##C##
    CreateBiTree(&T);// 建立二叉树，没有树，怎么遍历

    cout << "递归前序遍历输出为：" << endl;
    PreOrderTraverse(T, level);//进行前序遍历，其中operation1()和operation2()函数表示对遍历的结点数据进行的处理操作
    cout << endl;

    cout << "递归中序遍历输出为：" << endl;
    InOrderTraverse(T, level);
    cout << endl;

    cout << "递归后序遍历输出为：" << endl;
    PostOrderTraverse(T, level);
    cout << endl;

    return 0;
}
/*
请以前序遍历的方式输入扩展二叉树：
递归前序遍历输出为：
A在第1层
B在第2层
D在第3层
H在第4层
I在第4层
E在第3层
J在第4层
C在第2层
F在第3层
K在第4层
G在第3层

递归中序遍历输出为：
H在第4层
D在第3层
I在第4层
B在第2层
E在第3层
J在第4层
A在第1层
F在第3层
K在第4层
C在第2层
G在第3层

递归后序遍历输出为：
H在第4层
I在第4层
D在第3层
J在第4层
E在第3层
B在第2层
K在第4层
F在第3层
G在第3层
C在第2层
A在第1层

请按任意键继续. . .
*/

标签: 二叉树

好文要顶关注我收藏该文

flymey
关注 - 2
粉丝 - 1

+加关注

« 上一篇：SpringBoot简单连接数据库以及查询数据
» 下一篇：SpringBoot中过滤器、监听器以及拦截器

posted @ 2018-02-05 17:37 sky20080101 阅读(389) 评论(0) 收藏举报

刷新页面返回顶部

sky20080101

二叉树的四种遍历方法笔记 c实现树（二叉树）的建立和遍历算法（一）（前序，中序，后序）

c实现树（二叉树）的建立和遍历算法（一）（前序，中序，后序）

二叉树的四种遍历方法笔记

公告