题目整理-4
T1、公路修建
题面描述:
某国有 \(n\) 个城市,它们互相之间没有公路相通,因此交通十分不便。为解决这一“行路难”的问题,政府决定修建公路。修建公路的任务由各城市共同完成。
修建工程分若干轮完成。在每一轮中,每个城市选择一个与它最近的城市,申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。
政府审批的规则如下:
- 如果两个或以上城市申请修建同一条公路,则让它们共同修建;
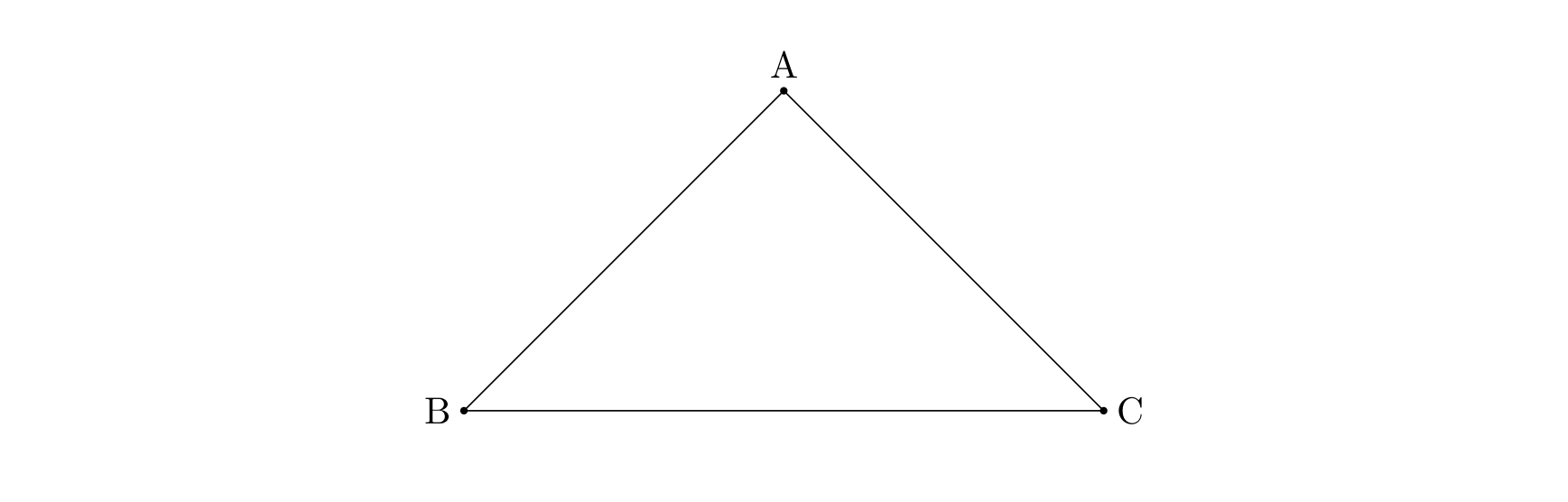
- 如果三个或以上的城市申请修建的公路成环。如下图,A 申请修建公路 AB,B 申请修建公路 BC,C 申请修建公路 CA。则政府将否决其中最短的一条公路的修建申请;
- 其他情况的申请一律同意。
一轮修建结束后,可能会有若干城市可以通过公路直接或间接相连。这些可以互相连通的城市即组成“城市联盟”。在下一轮修建中,每个“城市联盟”将被看作一个城市,发挥一个城市的作用。
当所有城市被组合成一个“城市联盟”时,修建工程也就完成了。
你的任务是根据城市的分布和前面讲到的规则,计算出将要修建的公路总长度。
思路:
易得,最后所有城市以及其相连的道路一定会形成树。
接下来分析形成环的条件。按照题意可得,此时这若干个城市之间一定之间的距离都是最近的,则不可能出现环内道路长度不同的情况,则无论否决那一条道路,情况都相同。
因此,可结合题意得出,此题需要求最小生成树。但是这个题卡 \(kruskal\),因此使用 \(prim\) 是最佳选择
标签:
最小生成树
prim
代码实现
this
#include<bits/stdc++.h>
#define N 5005
#define pr pair<int,int>
#define mr(a,b) make_pair(a,b)
#define ll long long
#define INF 0x3f3f3f3f
#define x first
#define y second
using namespace std;
int n,vis[N];
pr a[N];
double ans,dist[N];
double jl(pr t1,pr t2){
return sqrt((ll)(t1.x-t2.x)*(t1.x-t2.x)+(ll)(t1.y-t2.y)*(t1.y-t2.y));
}
void prim(){
dist[0]=INF;
dist[1]=0,vis[1]=1;
for(int i=2;i<=n;i++) dist[i]=jl(a[1],a[i]);
int m=n-1;
while(m--){
int mx=0;
for(int i=1;i<=n;i++) if(dist[i]<dist[mx]&&!vis[i]) mx=i;
ans+=dist[mx];
vis[mx]=1;
for(int i=1;i<=n;i++){
if(!vis[i]) dist[i]=min(dist[i],jl(a[mx],a[i]));
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i].x>>a[i].y;
prim();
printf("%.2f",ans);
return 0;
}
T2、兽径管理
题面描述:
在最开始给你 \(n\) 个点,没有边。给你 \(w\) 此操作,每一次操作为加入一条边并求出从一点开始可以将所有点经过的路径和的最小值。如果不存在,输出 \(-1\)。
思路:
非常明显的最小生成树。在每次加一次边后,重新跑一次最小生成树,复杂度允许。
标签:
最小生成树
kruskal
prim
代码实现
this
#include<bits/stdc++.h>
#define N 205
#define W 6005
#define pr3 pair<int,pair<int,int>>
#define mr3 make_pair(int,make_pair(int,int))
#define u second.first
#define v second.second
#define w first
using namespace std;
int n,w,m,b,f[N];
pr3 a[W];
int fd(int x){ return f[x]==x?x:(f[x]=fd(f[x])); }
int main(){
cin>>n>>w;
while(w--){
++m;
cin>>a[m].u>>a[m].v>>a[m].w;
int ans=0,t=n-1;
sort(a+1,a+m+1);
for(int i=1;i<=n;i++) f[i]=i;
for(int i=1;i<=m&&n;i++){
a[i].u=fd(a[i].u),a[i].v=fd(a[i].v);
if(a[i].u!=a[i].v) f[a[i].v]=a[i].u,t--,ans+=a[i].w;
}
if(!t) cout<<ans<<"\n";
else cout<<"-1\n";
}
return 0;
}
T3、[HNOI2006] 公路修建问题
题面描述:
给你 \(n\) 个点,\(m\) 对可连边的点。可连的边分为两类,一类的价格不会比二类低。此时你需要选择 \(n-1\) 条边,并且使得这 \(n-1\) 条边中有至少 \(k\) 条一类且最大的边权值最小。
思路:
先转化。因为最小生成树一定是瓶颈生成树,所以可以将题意化为:求至少包含 \(k\) 条一类边的最小生成树。
又因为对于同一对点,选择二类边一定比选择一类边更优,所以题意又可化为:求包含 \(k\) 条一类边的最小生成树。
贪心可以得到,先选 \(k\) 条一类边一定比先选二类边更优。所以结束
标签:
最小生成树
贪心
代码实现
this
#include<bits/stdc++.h>
#define N 10005
#define pr4 pair<pr,pr>
#define pr pair<int,int>
#define u second.first
#define v second.second
#define w first.first
#define num first.second
using namespace std;
int n,k,m,f[N],ans[N<<1],mx;
pr4 a[N<<1],b[N<<1];
int fd(int x){ return f[x]==x?x:(f[x]=fd(f[x])); }
int main(){
cin>>n>>k>>m;
m--;
for(int i=1;i<=m;i++){
cin>>a[i].u>>a[i].v>>a[i].w>>b[i].w;
b[i].second=a[i].second;
a[i].num=b[i].num=i;
}
sort(a+1,a+m+1);
sort(b+1,b+m+1);
for(int i=1;i<=n;i++) f[i]=i;
for(int i=1;i<=m&&k;i++){
a[i].u=fd(a[i].u),a[i].v=fd(a[i].v);
if(a[i].u!=a[i].v) f[a[i].v]=a[i].u,k--,ans[a[i].num]=1,mx=max(mx,a[i].w);
}
k=n-1-k;
for(int i=1;i<=m&&k;i++){
b[i].u=fd(b[i].u),b[i].v=fd(b[i].v);
if(b[i].u!=b[i].v) f[b[i].v]=b[i].u,k--,ans[b[i].num]=2,mx=max(mx,b[i].w);
}
cout<<mx<<"\n";
for(int i=1;i<=m;i++){
if(ans[i]) cout<<i<<" "<<ans[i]<<"\n";
}
return 0;
}
T4、逐个击破
题面描述:
给你一个 \(n\) 个点, \(m\) 条边的带权无向图,以及 \(k\) 个关键点。请你断开若干条边,使得这 \(k\) 个关键点互相无法到达。求最小花费。
思路:
类似 \(kruskal\)。
先将边按照递增排序,再逐渐加边。若此时加的边会使关键点联通,则不加,计入答案。
标签:
贪心
代码实现
this
#include<bits/stdc++.h>
#define N 100005
#define pr3 pair<int,pair<int,int>>
#define u second.first
#define v second.second
#define w first
#define ll long long
using namespace std;
int n,k,vis[N],f[N];
ll ans;
pr3 a[N];
int fd(int x){ return f[x]==x?x:(f[x]=fd(f[x])); }
int main(){
cin>>n>>k;
for(int i=1;i<=k;i++){
int t1;
cin>>t1;
t1++;
vis[t1]=1;
}
for(int i=1;i<n;i++){
cin>>a[i].u>>a[i].v>>a[i].w;
a[i].u++,a[i].v++,ans+=a[i].w;
}
sort(a+1,a+n);
for(int i=1;i<=n;i++) f[i]=i;
for(int i=n-1;i;i--){
a[i].u=fd(a[i].u),a[i].v=fd(a[i].v);
if(a[i].u!=a[i].v&&!(vis[a[i].u]&vis[a[i].v])){
f[a[i].v]=a[i].u;
vis[a[i].u]|=vis[a[i].v];
ans-=a[i].w;
}
}
cout<<ans;
return 0;
}
T5、[USACO19OPEN] I Would Walk 500 Miles G
题面描述:
Farmer John 想要将他的编号为 $ 1 \ldots N $ 的 $ N $ 头奶牛( $ N \leq 7500 $ )分为非空的 $ K $ 组( $ 2 \leq K \leq N $ ),使得任意两头来自不同组的奶牛都需要走一定的距离才能相遇。奶牛 $ x $ 和奶牛 $ y $ (其中 $ 1 \leq x<y \leq N $ )愿意为了见面走 $ (2019201913x+2019201949y) \mod 2019201997 $ 英里。
给定一个将 $ N $ 头奶牛分为 $ K $ 个非空小组的分组方案,令 $ M $ 为任意两头来自不同组的奶牛愿意为了见面行走的英里数的最小值。请你使 $ M $ 尽可能大。
思路:
我们可以先求出最小生成树。
若此时分成的两组奶牛 \(A,B\),则会发现,他们分成的这两组连线的最大值一定是最小生成树上的一条边。
因为要分为 \(k\) 组,所以最后还会剩下 \(k-1\)条边再树上。取其中的最小值即为答案。贪心易得,将最大的 \(k-1\) 条边放在外面一定是最优的。
标签:
最小生成树
贪心
代码实现
this
#include<bits/stdc++.h>
#define ll long long
#define N 7505
#define INF 0x3f3f3f3f3f3f3f3f
using namespace std;
ll n,k,ans,vis[N],dist[N];
ll tot,t[N];
ll jl(ll t1,ll t2){
if(t1>t2) swap(t1,t2);
return (2019201913*t1+2019201949*t2)%2019201997;
}
void prim(){
dist[0]=INF,dist[1]=0,vis[1]=1;
for(int i=2;i<=n;i++) dist[i]=jl(1,i);
ll m=n-1;
while(m--){
ll mn=0;
for(int i=1;i<=n;i++) if(dist[i]<dist[mn]&&!vis[i]) mn=i;
ans=max(ans,dist[mn]);
t[++tot]=dist[mn];
vis[mn]=1;
for(int i=1;i<=n;i++){
if(!vis[i]) dist[i]=min(dist[i],jl(mn,i));
}
}
sort(t+1,t+tot+1);
cout<<t[tot-k+2]<<"\n";
}
int main(){
cin>>n>>k;
prim();
return 0;
}
T6、[CSP-S2019 江西] 网格图
题面描述:
给你一个网格图,它的每列、每行的边值都相同。求该网格图的最小生成树。
思路:
根据求最小生成树 \(kruskal\) 算法,我们对所有边进行排序,很容易知道,在选择时,若这条边最优,则这一列/行也会最优。
但是,同样的,在该算法中,假如我们出现了环,则不会加入此边。放到该题上同理,但是会更简单一些,假设此时是列,则我们看之前添加的列的数量是否大于 \(1\),假如满足,才可能出现环。同时,也需要看行的数量是否大于 \(2\) 才可以。此时减的贡献即为行的数量减 \(1\)。(加入的是行同理)。
标签:
最小生成树
kruskal
代码实现
this
#include<bits/stdc++.h>
#define N 300005
#define pr pair<ll,ll>
#define x first
#define y second
#define ll long long
using namespace std;
int n,m;
ll ans;
pr a[N<<1];
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++) cin>>a[i].x,a[i].y=1;
for(int i=n+1;i<=n+m;i++) cin>>a[i].x;
sort(a+1,a+n+m+1);
ll t1=0,t2=0;
for(int i=1;i<=n+m;i++){
if(a[i].y){
ans+=a[i].x*(m-1);
if(t2>=2&&t1>=1) ans-=a[i].x*(t2-1);
t1++;
}
else{
ans+=a[i].x*(n-1);
if(t1>=2&&t2>=1) ans-=a[i].x*(t1-1);
t2++;
}
}
if(ans>=0) cout<<ans;
return 0;
}
T7、[IOI2014] game 游戏
题面描述:
有 \(n\) 个城市(编号为 \(0,\cdots,n−1\)),其中有些城市之间有航线。每个航线连接两个城市,并且是双向的。
梅玉可以问"城市 \(u\) 和 \(v\) 之间有直接航线吗?",健佳会立刻直接回答该问题。梅玉会询问每对城市恰好一次,因此总计会有 \(r = \frac{n (n−1)}{2}\) 个问题。如果由前 \(i\)(\(i<r\))个问题的答案可以推断出整个航空网是否连通,也就是说,是否任意一对城市之间都可以坐飞机互达(直接或间接),梅玉就获胜。否则意味着她需要知道全部 \(r\) 个回答,此时健佳获胜。
你的任务是,通过决定健佳如何回答,来帮助他赢得游戏。
思路:
首先有一些非常明显的性质。第一,你最后的航空网是一个树样子一定是最优的。第二,你让为真实的航线在一定范围内更向后放会更优。
但是,我们要求一个生成树呀,没有边权是不行的,结合上面的,我们容易想到按输入边的顺序赋递减的值,再求最小生成树,这样一定可以最优。
标签:
最小生成树
贪心
代码实现
this
#include<bits/stdc++.h>
#define pr3 pair<int,pair<int,int>>
#define w first
#define u second.first
#define v second.second
#define N 1505
using namespace std;
int n,m,f[N],ans[N*N];
pr3 a[N*N];
int find(int x){
return (f[x]==x)?x:(f[x]=find(f[x]));
}
int main(){
cin>>n;
m=(n)*(n-1)/2;
for(int i=1;i<=n;i++) f[i]=i;
for(int i=m;i;i--){
cin>>a[i].u>>a[i].v;
a[i].u++,a[i].v++,a[i].w=i;
}
sort(a+1,a+m+1);
n--;
for(int i=1;i<=m&&n;i++){
a[i].u=find(a[i].u),a[i].v=find(a[i].v);
if(a[i].u!=a[i].v){
f[a[i].v]=a[i].u;
ans[m-a[i].w+1]=1;
n--;
}
}
for(int i=1;i<=m;i++) cout<<ans[i]<<"\n";
return 0;
}
T8、[PA2014] Kuglarz
题面描述:
桌子上有 \(n\) 个杯子排成一行,编号为 \(1,2,…,n\),其中某些杯子底下藏有一个小球,如果你准确地猜出是哪些杯子,你就可以获得奖品。
花费 \(c_{ij}\) 元,你就可以知道杯子 \(i,i+1,…,j\) 底下藏有球的总数的奇偶性。
采取最优的询问策略,你至少需要花费多少元,才能保证猜出哪些杯子底下藏着球?
思路:
先尝试将操作简化。
操作分为两大种,一种为加,一种为减。
第一种,假设我们知道了 \([i,j],[j+1,k]\) 这两个区间,则可知道 \([i,k]\) 的信息。
第二种,假如我们知道了 \([i,j],[i,k]\ (j<k)\) 这两个区间,则可知道区间 \([j+1,k]\) 的信息。
但是,是不是有些麻烦?
因此,改变一下,使用左开右闭的区间方式,可将操作优化为:
第一种,假设我们知道了 \([i,j),[j,k)\) 这两个区间,则可知道 \([i,k)\) 的信息。
第二种,假如我们知道了 \([i,j),[i,k)\ (j<k)\) 这两个区间,则可知道区间 \([j,k)\) 的信息。
所以,此时我们其实可以通过任何一个 \(i,j\) 和 \(j,k\) 推出 \(i,k\)。但是这个题让求的是每一个 \([i,i+1)\) ,因此,我们可以想到,只要我们选择的所有区间的左右两个端点包含了从 \(1\) 至 \(n+1\) 的所有就可以了。
其实到这里,我们就不是很确定怎么搞了。因为你没有一个合适的算法来解决此类问题。没事,我们可以建图。将 \(1\) 至 \(n+1\) 各看为一个点,已知的区间可以看作边,最后的结果就可以看作求最小生成树。完美解决。
标签:
最小生成树
代码实现
this
#include<bits/stdc++.h>
#define N 2005
#define INF 0x3f3f3f3f
#define ll long long
using namespace std;
int n,mp[N][N];
int dist[N],vis[N];
ll ans;
void prim(){
for(int i=2;i<=n;i++) dist[i]=mp[1][i];
vis[1]=1,dist[0]=INF;
int t=n-1;
while(t--){
int mn=0;
for(int i=1;i<=n;i++){
if(!vis[i]&&dist[i]<dist[mn]) mn=i;
}
ans+=dist[mn];
vis[mn]=1;
for(int i=1;i<=n;i++){
if(!vis[i]&&mp[i][mn]<dist[i]) dist[i]=mp[i][mn];
}
}
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
for(int j=i;j<=n;j++){
cin>>mp[i][j+1];
mp[j+1][i]=mp[i][j+1];
}
}
n++;
prim();
cout<<ans;
return 0;
}
T9、[国家集训队] Tree I
题面描述:
给你 \(n\) 个点,\(m\) 条边,其中边有边权且分黑白两种颜色。现在请你求出恰好包含 \(k\) 条白边的最小生成树。
思路:
引用一句话:
这个题吧,说难也不难,说简单也不简单。
这个题最大的难点是如何控制白边的数量。但是,通过 \(kruskal\) 算法,我们可以想到,影响边的选择其实是跟边在排序后的位置有关。又因为此时我们需要控制白边的数量,于是我们此时就可以想到可否通过改变白边与黑边的相对位置,来控制选择的白边的数量。
答案显然是可行的。但是,在改变白边与黑边的相对位置时,不可能也不会改变白边的相对位置。因为你一旦改变白边的相对位置,此时的生成树就不一定是最优的。同理,黑边也是如此。
同时,在判断给白边加多少时,我们可以轻松发现:它是具有单调性的。因此,在外面套一个二分,里面一个最小生成树,就结束了。
标签:
最小生成树
二分
代码实现
this
#include<bits/stdc++.h>
#define pr4 pair<pair<int,int>,pair<int,int>>
#define N 50005
#define M 100005
#define w first.first
#define g first.second
#define u second.first
#define v second.second
using namespace std;
int n,m,k,ans;//k:need
int f[N];
pr4 a[M];
int find(int x){
return f[x]==x?x:(f[x]=find(f[x]));
}
int kruskal(){
int num=0;
ans=0;
for(int i=1;i<=m;i++){
int x=find(a[i].u),y=find(a[i].v);
if(x!=y){
// cout<<a[i].u<<" "<<a[i].v<<" "<<a[i].g<<"\n";
ans+=a[i].w;
f[y]=x;
if(!a[i].g) ++num;
}
}
// cout<<num<<": ";
return num;
}
int check(int mid){
for(int i=1;i<=m;i++){
if(!a[i].g) a[i].w+=mid;
}
sort(a+1,a+m+1);
for(int i=1;i<=n;i++) f[i]=i;
int t=kruskal();
for(int i=1;i<=m;i++){
if(!a[i].g) a[i].w-=mid;
}
return t>=k;
}
int main(){
cin>>n>>m>>k;
for(int i=1;i<=m;i++){
cin>>a[i].u>>a[i].v>>a[i].w>>a[i].g;
a[i].u++,a[i].v++;
}
int l=-100,r=100;
while(l<r){
int mid=(l+r+1)>>1;
if(check(mid)) l=mid;
else r=mid-1;
// cout<<l<<" "<<r<<"\n";
}
check(l);
cout<<ans-l*k;
return 0;
}
注:
- 题号为本校OJ上的链接,题名为原出处链接。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号