迪杰斯特拉(Dijkstra)算法

一 定义：求解一个指定的点到其他点的最短路径

　　　　不存在权值为负的边！！！

二 思想：每次对所有可见点的路径长度进行排序后，选择一条最短的路径。

看题：

第一行两个整数你n，m，分别表示顶点和边接下来m行，每行3个数下x,y,z,表示顶点x到顶点y的权值为z

样例：

6 9

1 2 1

1 3 12

2 3 9

2 4 3

3 5 5

4 3 4

4 5 13

4 6 15

5 6 4

从样例中我们可以画一个图

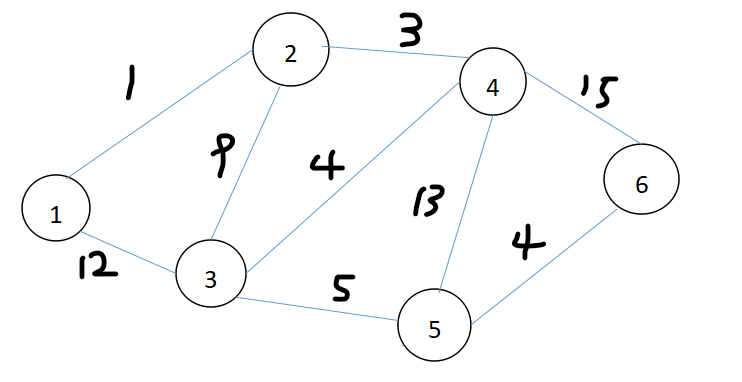
然后我们可以建立三个数组，e、dis、book

e数组用来储存顶点和顶点之间边的关系

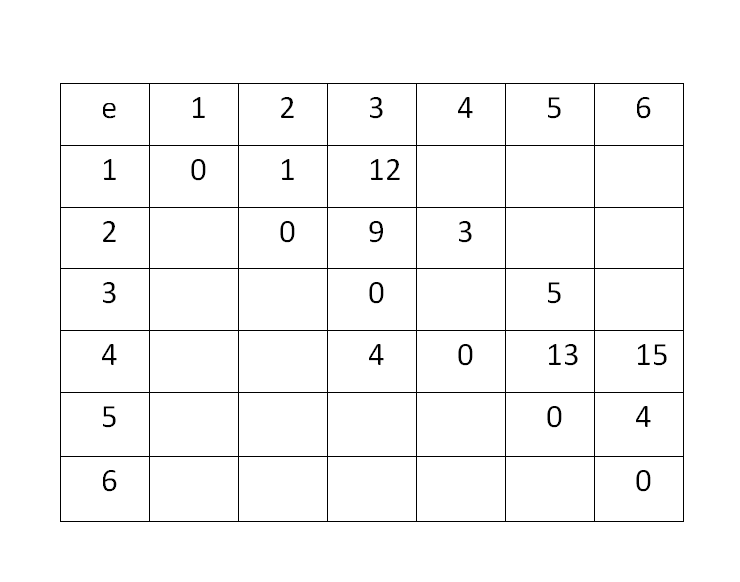
注：其余均为无穷

dis数组表示最短路径，dis中的值表示对最短路径的估计值

顶点分为已知和未知的，如果book[i]=1，表示已知最短路径的点，book[i]=0,表示未知最短路径的点

知道需要这三个数组后，我们就可以开始找点。

先找1号点可以直达且最近的点2号点，此时dis[2]的值就从估计值变为了确定值。

选中了2号点后，就以2号点为中心向四周扩展，我们看2→3，现在我们就发现，我们可以直接从1→3也可以通过2中转。

如果dis[3]>dis[2]+e[2][3],我们就对dis数组中的dis[3]的值进行更新。之后的点也是同一思路，先找点然后以找到的点为中心扩展。

上代码

#include<stdio.h>
int main()
{
    int dis[10];//储存最短路径 
    int e[10][10];//表示顶点与边的关系
    int book[10];//表示一个集合；如果book[i]=1，则为已知最短路，为0则未知
    int n,m,x,y,z,min,max=99999999;
    scanf("%d %d",&n,&m);
    // 初始化e数组，此时同一顶点距离为0，不同为无穷 
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=n;j++)
        {
            if(i==j) e[i][j]=0;
            else e[i][j]=max;
        }
    }
    //存图 
    for(int i=1;i<=m;i++)
    {
        scanf("%d %d %d",&x,&y,&z);
        e[x][y]=z;
    }
    //初始化dis数组，表示1号顶点到其他顶点的初始距离 
    for(int i=1;i<=n;i++)
    {
        dis[i]=e[1][i];
    }
    //初始化book数组，除源点本身为已知点，其余均未知 
    for(int i=1;i<=n;i++)
    {
        book[i]=0;
        book[1]=1;
    }
    //核心算法 
    for(int i=1;i<=n-1;i++)
    {
        int u,v;
        min=max;
        for(int j=1;j<=n;j++)
        {
            //最短路径的交换 
            if(book[j]==0&&dis[j]<min)
            {
                min=dis[j];
                u=j;
            }
        }
        book[u]=1;//改为已知点 
        for(v=1;v<=n;v++)
        {
            if(e[u][v]<max)//表示能够到达 
            {
                if(dis[v]>dis[u]+e[u][v]) dis[v]=dis[u]+e[u][v];
            }
        }
    }
    for(int i=1;i<=n;i++)
    {
        printf("%d ",dis[i]);
    }
    return 0;
}

运行结果：

0  1  8  4  13  17