莫烦Pytorch 2.建造第一个神经网络
1.关系拟合(回归)
建立数据集
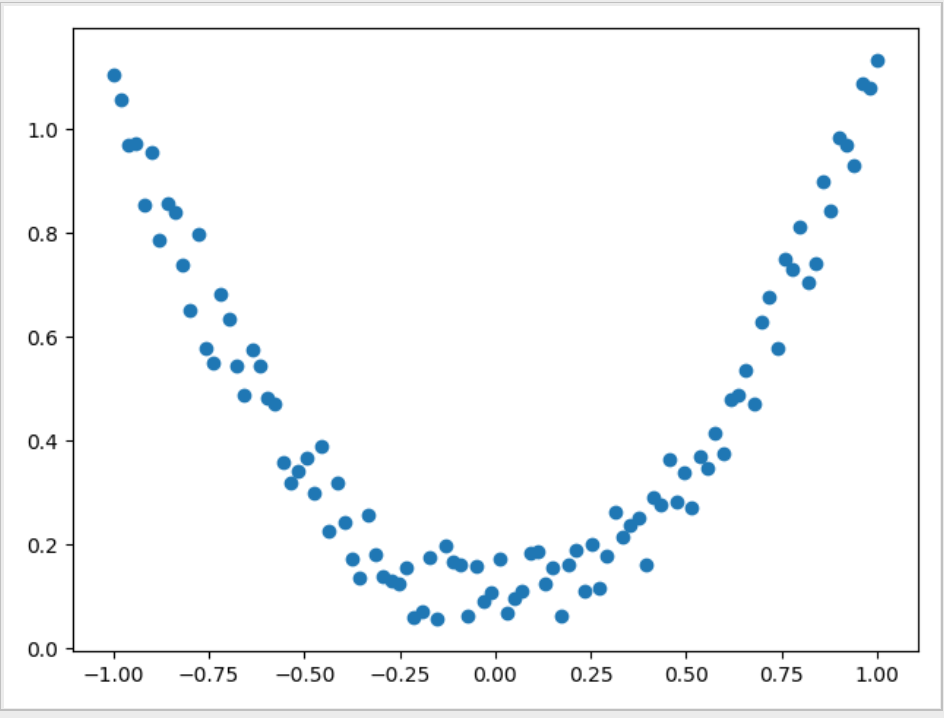
我们创建一些假数据来模拟真实的情况. 比如一个一元二次函数: y = a * x^2 + b, 我们给 y 数据加上一点噪声来更加真实的展示它.
import torch
import matplotlib.pyplot as plt
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
# 画图
plt.scatter(x.data.numpy(), y.data.numpy())
plt.show()
建立神经网络
建立一个神经网络我们可以直接运用 torch 中的体系. 先定义所有的层属性(__init__()), 然后再一层层搭建(forward(x))层与层的关系链接.
class Net(torch.nn.Module): # 继承torch的 Module
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()# 继承 __init__ 功能
# 自己定义每层用什么样的形式
self.hidden = torch.nn.Linear(n_feature,n_hidden) # 隐藏层线性输出
self.predict= torch.nn.Linear(n_hidden, n_output) # 输出层线性输出
def forward(self, x): #这同时也是Module中的forward功能 前向传播 搭神经网络
# 正向传播输入值, 神经网络分析出输出值
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.predict(x) # 输出值
return x
net = Net(n_feature=1,n_hidden=10,n_output=1)
print(net) # net 的结构
"""
Net(
(hidden): Linear(in_features=1, out_features=10, bias=True)
(predict): Linear(in_features=10, out_features=1, bias=True)
)
"""
训练网络
训练的步骤很简单, 如下:
# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(),lr=0.2) # 传入net的所有参数, 学习率
loss_func = torch.nn.MSELoss() # 预测值和真实值的误差计算公式 (均方差)
for t in range(100):
prediction = net(x) # 喂给 net 训练数据 x, 输出预测值
loss = loss_func(prediction, y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
可视化训练过程
为了可视化整个训练的过程, 更好的理解是如何训练, 我们如下操作:
plt.ion() #设置为实时感应
plt.show()
optimizer = torch.optim.SGD(net.parameters(),lr=0.5) # 传入net的所有参数, 学习率
loss_func = torch.nn.MSELoss() # 预测值和真实值的误差计算公式 (均方差)
for t in range(200):
prediction = net(x) # 喂给 net 训练数据 x, 输出预测值
loss = loss_func(prediction, y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
if t % 5 == 0:
plt.cla()
plt.scatter(x.data.numpy(), y.data.numpy()) #散点图
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5) #预测图
plt.text(0.5, 0, 'Loss=%.4f' % loss.data.numpy(),fontdict={'size': 20, 'color':'red'})#文字
plt.pause(0.2)
plt.ioff()
plt.show()
2.区分类型(分类)
import torch
import matplotlib.pyplot as plt
import torch.nn.functional as F
建立数据集
我们创建一些假数据来模拟真实的情况. 比如两个二次分布的数据, 不过他们的均值都不一样.
# 假数据
n_data = torch.ones(100,2) # (100,2)全为1的张量
x0 = torch.normal(2*n_data,1) # 类型0 x data (tensor), shape=(100,2)
y0 = torch.zeros(100) # 类型0 y data (tensor), shape=(100,)
x1 = torch.normal(-2*n_data,1) # 类型1 x data (tensor), shape=(100,1)
y1 = torch.ones(100) # 类型1 y data (tensor), shape=(100,)
# print(n_data)
# print(x0)
# print(y0)
# print(x1)
# print(y1)
# 注意 x, y 数据的数据形式是一定要像下面一样 (torch.cat 是在合并数据)
x = torch.cat((x0, x1),0).type(torch.FloatTensor) # FloatTensor = 32-bit floating
y = torch.cat((y0, y1), ).type(torch.LongTensor) # LongTensor = 64-bit integer
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=y.data.numpy(), s=100, lw=0, cmap='RdYlGn')
plt.show()
建立神经网络
建立一个神经网络我们可以直接运用 torch 中的体系. 先定义所有的层属性(__init__()), 然后再一层层搭建(forward(x))层于层的关系链接. 这个和我们在前面 regression 的时候的神经网络基本没差.
class Net(torch.nn.Module): # 继承 torch 的 Module
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__() # 继承 __init__ 功能
self.hidden = torch.nn.Linear(n_feature, n_hidden) # 隐藏层线性输出
self.out = torch.nn.Linear(n_hidden, n_output) # 输出层线性输出
def forward(self, x):
# 正向传播输入值, 神经网络分析出输出值
x = F.relu(self.hidden(x)) # 激励函数(隐藏层的线性值)
x = self.out(x) # 输出值, 但是这个不是预测值, 预测值还需要再另外计算
return x
net = Net(n_feature=2, n_hidden=10, n_output=2) # 几个类别就几个 output
print(net) # net 的结构
"""
Net(
(hidden): Linear(in_features=2, out_features=10, bias=True)
(out): Linear(in_features=10, out_features=2, bias=True)
)
"""
训练网络
训练的步骤很简单, 如下:
# optimizer 是训练的工具
optimizer = torch.optim.SGD(net.parameters(), lr=0.02) # 传入 net 的所有参数, 学习率
# 算误差的时候, 注意真实值!不是! one-hot 形式的, 而是1D Tensor, (batch,)
# 但是预测值是2D tensor (batch, n_classes)
loss_func = torch.nn.CrossEntropyLoss()#分类问题,交叉熵(softmax)
for t in range(100):
out = net(x) # 喂给 net 训练数据 x, 输出分析值
loss = loss_func(out, y) # 计算两者的误差
optimizer.zero_grad() # 清空上一步的残余更新参数值
loss.backward() # 误差反向传播, 计算参数更新值
optimizer.step() # 将参数更新值施加到 net 的 parameters 上
可视化训练过程
为了可视化整个训练的过程, 更好的理解是如何训练, 我们如下操作:
optimizer = torch.optim.SGD(net.parameters(), lr=0.02)
loss_func = torch.nn.CrossEntropyLoss() # the target label is NOT an one-hotted
plt.ion() # something about plotting
for t in range(10):
out = net(x) # input x and predict based on x
loss = loss_func(out, y) # must be (1. nn output, 2. target), the target label is NOT one-hotted
optimizer.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
optimizer.step() # apply gradients
if t % 2 == 0:
# plot and show learning process
plt.cla()
prediction = torch.max(F.softmax(out), 1)[1]
pred_y = prediction.data.numpy()
target_y = y.data.numpy()
plt.scatter(x.data.numpy()[:, 0], x.data.numpy()[:, 1], c=pred_y, s=100, lw=0, cmap='RdYlGn')
accuracy = float((pred_y == target_y).astype(int).sum()) / float(target_y.size)
plt.text(1.5, -4, 'Accuracy=%.2f' % accuracy, fontdict={'size': 20, 'color': 'red'})
plt.pause(0.1)
plt.ioff()
plt.show()
3.快速搭建法
快速搭建
我们先看看之前写神经网络时用到的步骤. 我们用 net1 代表这种方式搭建的神经网络.
class Net(torch.nn.Module):
def __init__(self, n_feature, n_hidden, n_output):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(n_feature, n_hidden) # hidden layer
self.predict = torch.nn.Linear(n_hidden, n_output) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
net1 = Net(1, 10, 1)
我们用 class 继承了一个 torch 中的神经网络结构, 然后对其进行了修改, 不过还有更快的一招, 用一句话就概括了上面所有的内容!
net2 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
我们再对比一下两者的结构:
print(net1) # net1 architecture
"""
Net(
(hidden): Linear(in_features=1, out_features=10, bias=True)
(predict): Linear(in_features=10, out_features=1, bias=True)
)
"""
print(net2) # net2 architecture
"""
Sequential(
(0): Linear(in_features=1, out_features=10, bias=True)
(1): ReLU()
(2): Linear(in_features=10, out_features=1, bias=True)
)
"""
我们会发现 net2 多显示了一些内容, 这是为什么呢? 原来他把激励函数也一同纳入进去了, 但是 net1 中, 激励函数实际上是在 forward() 功能中才被调用的. 这也就说明了, 相比 net2, net1 的好处就是, 你可以根据你的个人需要更加个性化你自己的前向传播过程, 比如(RNN). 不过如果你不需要七七八八的过程, 相信 net2 这种形式更适合你.
4.保存提取
保存
我们快速地建造数据, 搭建网络:
#假数据
x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim=1) # x data (tensor), shape=(100, 1)
y = x.pow(2) + 0.2*torch.rand(x.size()) # noisy y data (tensor), shape=(100, 1)
def save():
net1 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
optimizer = torch.optim.SGD(net1.parameters(), lr=0.5)
loss_func = torch.nn.MSELoss()
for t in range(100):
prediction = net1(x)
loss = loss_func(prediction, y)
optimizer.zero_grad()
loss.backward()
optimizer.step()
# plot result
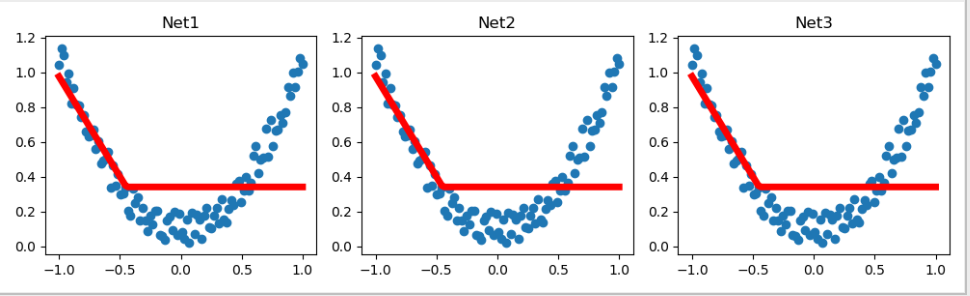
plt.figure(1, figsize=(10, 3))
plt.subplot(131)
plt.title('Net1')
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
接下来我们有两种途径来保存
torch.save(net1, 'net.pkl') # 保存整个网络
torch.save(net1.state_dict(),'net_params.pkl')#只保存参数
提取网络
这种方式将会提取整个神经网络, 网络大的时候可能会比较慢.
def restore_net():
#恢复神经网络 net1->net2
net2 = torch.load('net.pkl')
prediction = net2(x)
# plot result
plt.subplot(132)
plt.title('Net2')
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
只提取网络参数
这种方式将会提取所有的参数, 然后再放到你的新建网络中.
def restore_params():
#恢复神经网络 net1 to net3
net3 = torch.nn.Sequential(
torch.nn.Linear(1, 10),
torch.nn.ReLU(),
torch.nn.Linear(10, 1)
)
# copy net1's parameters into net3
net3.load_state_dict(torch.load('net_params.pkl'))
prediction = net3(x)
# plot result
plt.subplot(133)
plt.title('Net3')
plt.scatter(x.data.numpy(), y.data.numpy())
plt.plot(x.data.numpy(), prediction.data.numpy(), 'r-', lw=5)
plt.show()
显示结果
调用上面建立的几个功能, 然后出图,看出三个网络完全一模一样。
5.批训练
Torch 中提供了一种帮你整理你的数据结构的好东西, 叫做 DataLoader, 我们能用它来包装自己的数据, 进行批训练.。
DataLoader
DataLoader 是 torch 给你用来包装你的数据的工具. 所以你要讲自己的 (numpy array 或其他) 数据形式装换成 Tensor, 然后再放进这个包装器中. 使用 DataLoader 有什么好处呢? 就是他们帮你有效地迭代数据, 举例:
import torch
import torch.utils.data as Data
torch.manual_seed(1) # reproducible
BATCH_SIZE = 5
# BATCH_SIZE = 8
x = torch.linspace(1, 10, 10) # this is x data (torch tensor)
y = torch.linspace(10, 1, 10) # this is y data (torch tensor)
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(
dataset=torch_dataset, # torch TensorDataset format
batch_size=BATCH_SIZE, # mini batch size
shuffle=True, # random shuffle for training
num_workers=2, # subprocesses for loading data
)
def show_batch():
for epoch in range(3): # train entire dataset 3 times
for step, (batch_x, batch_y) in enumerate(loader): # for each training step
# train your data...
print('Epoch: ', epoch, '| Step: ', step, '| batch x: ',
batch_x.numpy(), '| batch y: ', batch_y.numpy())
if __name__ == '__main__':
show_batch()
6.优化器加速神经网络训练
今天我们会来聊聊在怎么样加速你的神经网络训练过程.
包括以下几种模式:
- Stochastic Gradient Descent (SGD)
- Momentum
- AdaGrad
- RMSProp
- Adam
越复杂的神经网络 , 越多的数据 , 我们需要在训练神经网络的过程上花费的时间也就越多. 原因很简单, 就是因为计算量太大了. 可是往往有时候为了解决复杂的问题, 复杂的结构和大数据又是不能避免的, 所以我们需要寻找一些方法, 让神经网络聪明起来, 快起来.
1.Stochastic Gradient Descent (SGD)
最基础的方法就是 SGD 啦, 想像红色方块是我们要训练的 data, 如果用普通的训练方法, 就需要重复不断的把整套数据放入神经网络 NN训练, 这样消耗的计算资源会很大.
我们换一种思路, 如果把这些数据拆分成小批小批的, 然后再分批不断放入 NN 中计算, 这就是我们常说的 SGD 的正确打开方式了. 每次使用批数据, 虽然不能反映整体数据的情况, 不过却很大程度上加速了 NN 的训练过程, 而且也不会丢失太多准确率.
2.Momentum
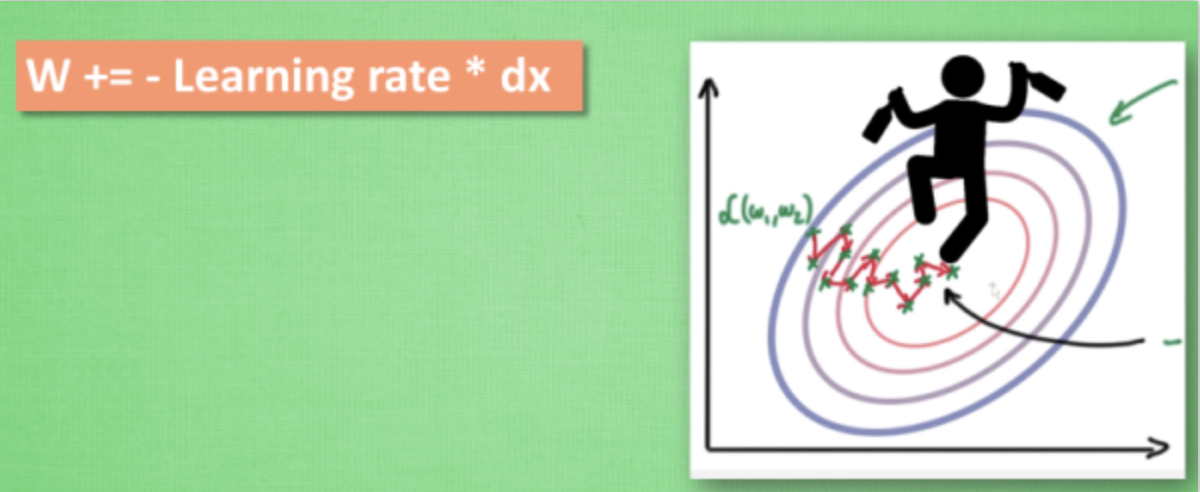
大多数其他途径是在更新神经网络参数那一步上动动手脚. 传统的参数 W 的更新是把原始的 W 累加上一个负的学习率(learning rate) 乘以校正值 (dx). 这种方法可能会让学习过程曲折无比, 看起来像 喝醉的人回家时, 摇摇晃晃走了很多弯路.
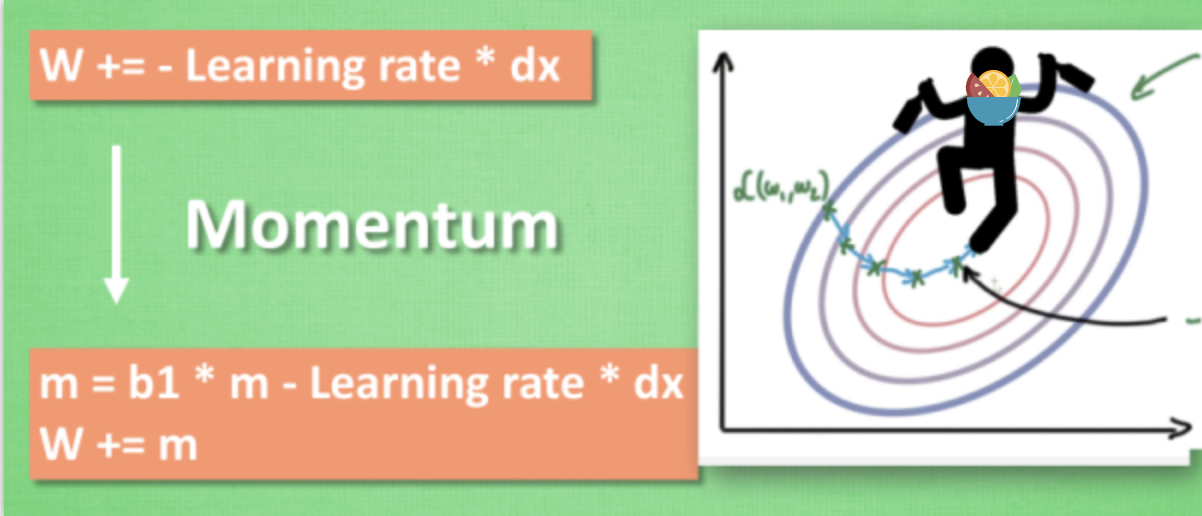
所以我们把这个人从平地上放到了一个斜坡上, 只要他往下坡的方向走一点点, 由于向下的惯性, 他不自觉地就一直往下走, 走的弯路也变少了. 这就是 Momentum 参数更新. 另外一种加速方法叫AdaGrad.
3.AdaGrad

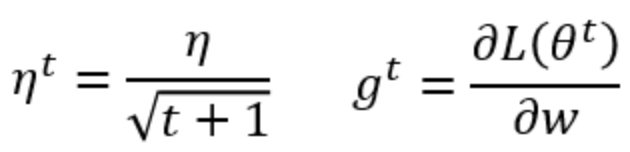
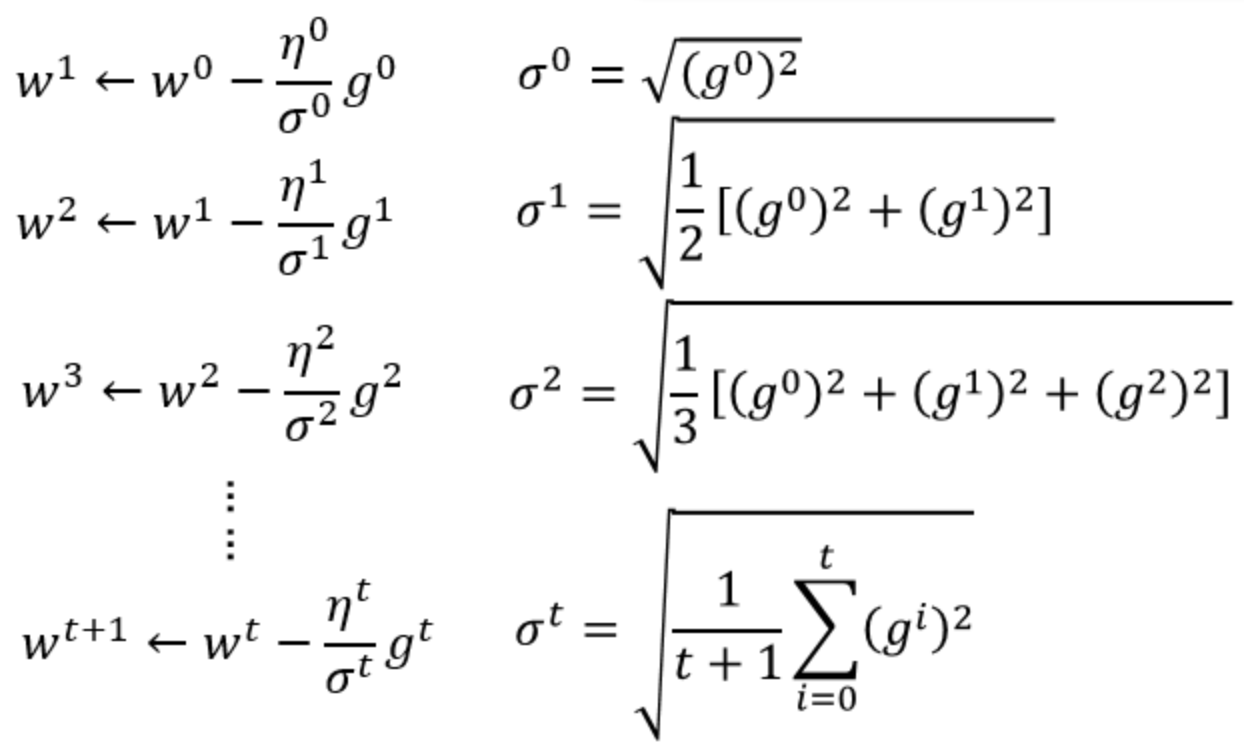
这种方法是在学习率上面动手脚, 使得每一个参数更新都会有自己与众不同的学习率, 他的作用和 momentum 类似, 不过不是给喝醉酒的人安排另一个下坡, 而是给他一双不好走路的鞋子, 使得他一摇晃着走路就脚疼, 鞋子成为了走弯路的阻力, 逼着他往前直着走. 他的数学形式是这样的. 接下来又有什么方法呢? 如果把下坡和不好走路的鞋子合并起来, 是不是更好呢? 没错, 这样我们就有了 RMSProp 更新方法.
4.RMSProp
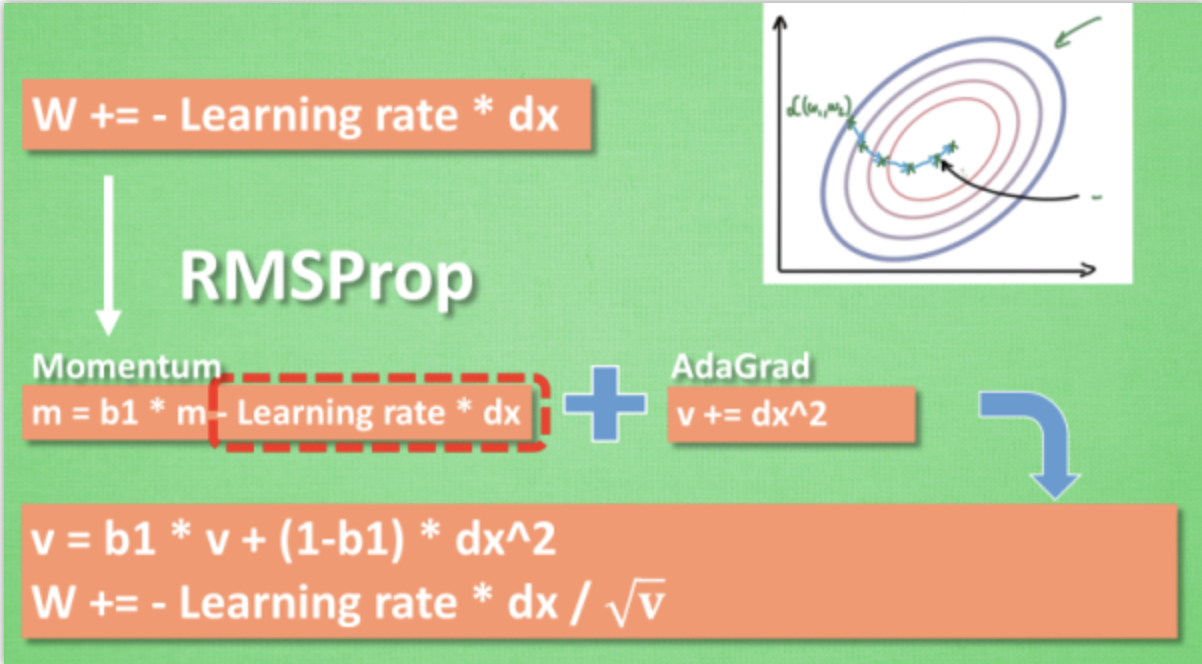
有了 momentum 的惯性原则 , 加上 adagrad 的对错误方向的阻力, 我们就能合并成这样. 让 RMSProp同时具备他们两种方法的优势. 不过细心的同学们肯定看出来了, 似乎在 RMSProp 中少了些什么. 原来是我们还没把 Momentum合并完全, RMSProp 还缺少了 momentum 中的 这一部分. 所以, 我们在 Adam 方法中补上了这种想法.
5.Adam
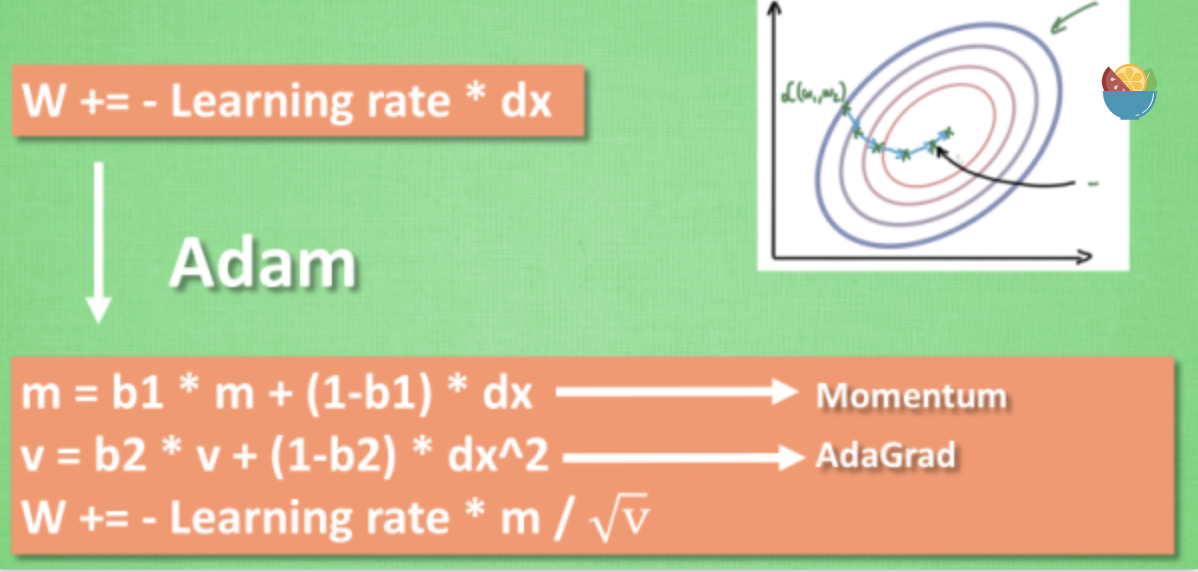
计算m 时有 momentum 下坡的属性, 计算 v 时有 adagrad 阻力的属性, 然后再更新参数时 把 m 和 V 都考虑进去. 实验证明, 大多数时候, 使用 adam 都能又快又好的达到目标, 迅速收敛. 所以说, 在加速神经网络训练的时候, 一个下坡, 一双破鞋子, 功不可没.
7.优化器
import torch
import torch.utils.data as Data
import torch.nn.functional as F
import matplotlib.pyplot as plt
伪数据
为了对比各种优化器的效果, 我们需要有一些数据, 今天我们还是自己编一些伪数据, 这批数据是这样的:
LR = 0.01
BATCH_SIZE = 32
EPOCH = 12
# fake dataset
x = torch.unsqueeze(torch.linspace(-1, 1, 1000), dim=1)
y = x.pow(2) + 0.1*torch.normal(torch.zeros(*x.size()))
# plot dataset
plt.scatter(x.numpy(), y.numpy())
plt.show()
# put dateset into torch dataset
torch_dataset = Data.TensorDataset(x, y)
loader = Data.DataLoader(dataset=torch_dataset, batch_size=BATCH_SIZE, shuffle=True, num_workers=2,)
每个优化器优化一个神经网络
为了对比每一种优化器, 我们给他们各自创建一个神经网络, 但这个神经网络都来自同一个 Net 形式.
# default network
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.hidden = torch.nn.Linear(1, 20) # hidden layer
self.predict = torch.nn.Linear(20, 1) # output layer
def forward(self, x):
x = F.relu(self.hidden(x)) # activation function for hidden layer
x = self.predict(x) # linear output
return x
if __name__ == '__main__':
# different nets
net_SGD = Net()
net_Momentum = Net()
net_RMSprop = Net()
net_Adam = Net()
nets = [net_SGD, net_Momentum, net_RMSprop, net_Adam]
优化器
接下来在创建不同的优化器, 用来训练不同的网络. 并创建一个 loss_func 用来计算误差. 我们用几种常见的优化器, SGD, Momentum, RMSprop, Adam.
# different optimizers
opt_SGD = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))
optimizers = [opt_SGD, opt_Momentum, opt_RMSprop, opt_Adam]
loss_func = torch.nn.MSELoss()
losses_his = [[], [], [], []] # record loss
训练/出图
接下来训练和 loss 画图.
# training
for epoch in range(EPOCH):
print('Epoch: ', epoch)
for step, (b_x, b_y) in enumerate(loader): # for each training step
for net, opt, l_his in zip(nets, optimizers, losses_his):
output = net(b_x) # get output for every net
loss = loss_func(output, b_y) # compute loss for every net
opt.zero_grad() # clear gradients for next train
loss.backward() # backpropagation, compute gradients
opt.step() # apply gradients
l_his.append(loss.data.numpy()) # loss recoder
labels = ['SGD', 'Momentum', 'RMSprop', 'Adam']
for i, l_his in enumerate(losses_his):
plt.plot(l_his, label=labels[i])
plt.legend(loc='best')
plt.xlabel('Steps')
plt.ylabel('Loss')
plt.ylim((0, 0.2))
plt.show()
SGD 是最普通的优化器, 也可以说没有加速效果, 而 Momentum 是 SGD 的改良版, 它加入了动量原则. 后面的 RMSprop 又是 Momentum 的升级版. 而 Adam 又是 RMSprop 的升级版. 不过从这个结果中我们看到, Adam 的效果似乎比 RMSprop 要差一点. 所以说并不是越先进的优化器, 结果越佳. 我们在自己的试验中可以尝试不同的优化器, 找到那个最适合你数据/网络的优化器.






 浙公网安备 33010602011771号
浙公网安备 33010602011771号