POJ3009 DFS解
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 5792 | Accepted: 2381 |
Description
On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.
Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)
The movement of the stone obeys the following rules:
- At the beginning, the stone stands still at the start square.
- The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
- When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. 2(a)).
- Once thrown, the stone keeps moving to the same direction until one of the following occurs:
- The stone hits a block (Fig. 2(b), (c)).
- The stone stops at the square next to the block it hit.
- The block disappears.
- The stone gets out of the board.
- The game ends in failure.
- The stone reaches the goal square.
- The stone stops there and the game ends in success.
- The stone hits a block (Fig. 2(b), (c)).
- You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.
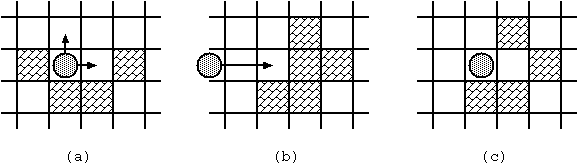
Fig. 2: Stone movements
Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.
With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).
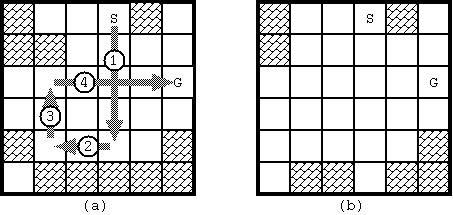
Fig. 3: The solution for Fig. D-1 and the final board configuration
Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.
Each dataset is formatted as follows.
the width(=w) and the height(=h) of the board
First row of the board
...
h-th row of the board
The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.
Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.
0 vacant square 1 block 2 start position 3 goal position
The dataset for Fig. D-1 is as follows:
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
Output
For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.
Sample Input
2 1 3 2 6 6 1 0 0 2 1 0 1 1 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 1 0 0 0 0 1 0 1 1 1 1 1 6 1 1 1 2 1 1 3 6 1 1 0 2 1 1 3 12 1 2 0 1 1 1 1 1 1 1 1 1 3 13 1 2 0 1 1 1 1 1 1 1 1 1 1 3 0 0
Sample Output
1 4 -1 4 10 -1
Source
这道题网上大部分解法都是用的BFS,但个人感觉这道题的数据量还有条件都表示可以用DFS来解。
最终成绩:
Accepted 664K 235MS G++ 6003B
个人总结需要注意到的点:冰球撞到石头后会把石头摧毁,并停在石头前。
例: 如果有这样一个阵列:
0 0 0 9 0 0 1
0代表空位,9代表冰球,1代表石头,那么向右击球会让阵列变成这样:
0 0 0 0 0 9 0
明白了这点就很好解了。
对自己一点点不满:end其实不用当参数传,用全局变量也可,还能省一点栈空间。。。
 View Code
View Code
1 #include<iostream>
2 #include<cstdio>
3 #include<cstring>
4 #include<queue>
5 #define MAXN 25
6 using namespace std;
7 const short dir[][2]={{-1,0},{1,0},{0,-1},{0,1}};
8 long m,n;
9 struct node
10 {
11 long x,y;
12 };
13 long square[MAXN][MAXN];
14 bool check(node s)
15 {
16 if(s.x>=m||s.y>=n||s.x<0||s.y<0)
17 return false;
18 if(square[s.x][s.y]==1)
19 return false;
20 return true;
21 }
22 long dfs(node st,node end,long step)
23 {
24 if(step>10)
25 return -1;
26 if(st.x==end.x&&st.y==end.y)
27 return step;
28 node p;
29 long ans=9999999;
30 long st_x,st_y;
31 for(long i=0;i!=4;i++)
32 {
33 p.x=st.x+dir[i][0];p.y=st.y+dir[i][1];
34 if(check(p))
35 {
36 if(i==0)//up
37 {
38 for(long j=p.x;j!=-1;j--)
39 {
40 if(square[j][p.y]==1)
41 {
42 st_x=j,st_y=p.y;
43 square[st_x][st_y]=0;
44 p.x=j+1;
45 long temp=dfs(p,end,step+1);
46 square[st_x][st_y]=1;
47 if(ans>temp&&(temp!=-1))
48 ans=temp;
49 break;
50 }
51 else if(square[j][p.y]==3)
52 {
53 if(ans>step+1)
54 ans=step+1;
55 break;
56 }
57 }
58 }
59 else if(i==1)//down
60 {
61 for(long j=p.x;j!=m;j++)
62 {
63 if(square[j][p.y]==1)
64 {
65 st_x=j,st_y=p.y;
66 square[st_x][st_y]=0;
67 p.x=j-1;
68 long temp=dfs(p,end,step+1);
69 square[st_x][st_y]=1;
70 if(ans>temp&&(temp!=-1))
71 ans=temp;
72 break;
73 }
74 else if(square[j][p.y]==3)
75 {
76 if(ans>step+1)
77 ans=step+1;
78 break;
79 }
80 }
81 }
82 else if(i==2)//left
83 {
84 for(long j=p.y;j!=-1;j--)
85 {
86 if(square[p.x][j]==1)
87 {
88 st_x=p.x,st_y=j;
89 square[st_x][st_y]=0;
90 p.y=j+1;
91 long temp=dfs(p,end,step+1);
92 square[st_x][st_y]=1;
93 if(ans>temp&&(temp!=-1))
94 ans=temp;
95 break;
96 }
97 else if(square[p.x][j]==3)
98 {
99 if(ans>step+1)
100 ans=step+1;
101 break;
102 }
103 }
104 }
105 else if(i==3)//right
106 {
107 for(long j=p.y;j!=n;j++)
108 {
109 if(square[p.x][j]==1)
110 {
111 st_x=p.x,st_y=j;
112 square[st_x][st_y]=0;
113 p.y=j-1;
114 long temp=dfs(p,end,step+1);
115 square[st_x][st_y]=1;
116 if(ans>temp&&(temp!=-1))
117 ans=temp;
118 break;
119 }
120 else if(square[p.x][j]==3)
121 {
122 if(ans>step+1)
123 ans=step+1;
124 break;
125 }
126 }
127 }
128 }
129 }
130 if(ans==9999999||ans>10)
131 return -1;
132 return ans;
133 }
134 int main(void)
135 {
136 node start,end;
137 while(scanf("%ld%ld",&n,&m)==2)
138 {
139 if(n==0&&m==0)
140 break;
141 memset(square,0,sizeof(square));
142 for(long i=0;i!=m;i++)
143 for(long j=0;j!=n;j++)
144 {
145 scanf("%ld",&square[i][j]);
146 if(square[i][j]==2)
147 {
148 start.x=i;start.y=j;
149 }
150 else
151 if(square[i][j]==3)
152 {
153 end.x=i;end.y=j;
154 }
155 }
156 printf("%ld\n",dfs(start,end,0));
157 }
158 return 0;
159 }
posted on 2011-10-28 21:39 SilVeRyELF 阅读(170) 评论(0) 收藏 举报




 浙公网安备 33010602011771号
浙公网安备 33010602011771号