3D空间绕过原点的轴逆时针旋转的矩阵推导

构建出绕轴旋转的情景。

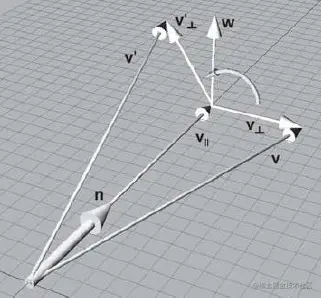
向量v绕轴n 逆时针旋转θ角度后得到向量v',注：n为单位向量。

想要解v'， 可以通过向量加法得到。易得v' 在向量n方向的投影 。 还需要构造一个经过v' 端点 ， 垂直于法线n的平面，在这个平面内，v的端点绕向量n旋转了θ度后 ， 就是v' 的端点 。n与平面的交点为O'， 那么再求得V' 端点与O' 点构成的向量 ， 就可以得到v' 了。

定义：

$v_{\bot}$是v在于n垂直的平面内的投影

$v_{\text{\textbardbl}}$是v' 在n上的投影，等价于v在n上的投影

$v'_{\bot}$是v' 在于n垂直的平面内的投影

$v_{\bot}$绕n旋转θ度后得到$v'_{\bot}$

想要求得$v'_{\bot}$，只需要组成一个w，与 n 和 ****$v_{\bot}$组成坐标系就可以 。

$w = v_{\bot} \times n$

那么

$v'_{\bot} = v_{\bot}\cos\theta + w\sin\theta$

根据上面的定义，求出来$v_{\bot}$和w，带入公式。

$v_{\text{\textbardbl}} = (v \cdot n)n$

$v_{\bot} = v - v_{\text{\textbardbl}} = v - (v \cdot n)n$

$w = v_{\bot} \times n = (v - (v \cdot n)n) \times n = v\times n$

即

$v'_{\bot} = v_{\bot}\cos\theta + w\sin\theta = (v - (v \cdot n)n)\cos\theta + (v \times n) \sin \theta$

$v' = v_{\text{\textbardbl}} + v'_{\bot} = (v \cdot n) n + (v - (v \cdot n)n)\cos\theta + (v \times n) \sin \theta = v\cos\theta + (v\cdot n)n(1-\cos\theta) + (v\times n)\sin\theta$

将基向量(1, 0, 0), (0, 1, 0), (0, 0 , 1)带入公式分别求得新的基向量，即得旋转矩阵。

令$v = \begin {bmatrix}\ 1 \\ 0 \\ 0 \end{bmatrix}$，代入上式得

$v' = \begin {bmatrix}\ 1 \\ 0 \\ 0 \end{bmatrix} \cos\theta + \begin {bmatrix}\ 1& 0 & 0 \end{bmatrix}\begin {bmatrix}\ n_x \\ n_y \\ n_z \end{bmatrix} \begin {bmatrix}\ n_x \\ n_y \\ n_z \end{bmatrix} (1 - \cos \theta) + \begin {bmatrix}\ 1 \\ 0 \\ 0 \end{bmatrix} \times \begin {bmatrix}\ n_x \\ n_y \\ n_z \end{bmatrix} \sin \theta$

$= \begin {bmatrix}\ \cos\theta \\ 0 \\ 0 \end{bmatrix} + \begin {bmatrix}\ n_x^2 \\ n_xn_y \\ n_xn_z \end{bmatrix} (1 - \cos \theta) + \begin {bmatrix}\ 0 \\ -n_z \\ n_y \end{bmatrix} \sin \theta$

$= \begin {bmatrix}\ n_x^2(1-\cos\theta) + \cos\theta \\ n_xny_(1-\cos\theta) -n_z\sin\theta \\ n_xn_z(1-\cos\theta) + n_y\sin\theta \end{bmatrix}$

令$v = \begin {bmatrix}\ 0 \\ 1 \\ 0 \end{bmatrix}$，代入上式得

$v' = \begin {bmatrix}\ 0 \\ 1 \\ 0 \end{bmatrix} \cos\theta + \begin {bmatrix}\ 0& 1 & 0 \end{bmatrix}\begin {bmatrix}\ n_x \\ n_y \\ n_z \end{bmatrix} \begin {bmatrix}\ n_x \\ n_y \\ n_z \end{bmatrix} (1 - \cos \theta) + \begin {bmatrix}\ 0 \\ 1 \\ 0 \end{bmatrix} \times \begin {bmatrix}\ n_x \\ n_y \\ n_z \end{bmatrix} \sin \theta$

$= \begin {bmatrix}\ 0 \\ \cos\theta \\ 0 \end{bmatrix} + \begin {bmatrix}\ n_xn_y \\ n_y^2 \\ n_yn_z \end{bmatrix} (1 - \cos \theta) + \begin {bmatrix}\ n_z \\ 0 \\ -n_x \end{bmatrix} \sin \theta$

$= \begin {bmatrix}\ n_xn_z(1-\cos\theta) + n_z\sin\theta \\ n_y^2(1-\cos\theta) + \cos\theta \\ n_yn_z(1-\cos\theta) -n_x \sin\theta \end{bmatrix}$

令$v = \begin {bmatrix}\ 0 \\ 0 \\ 1 \end{bmatrix}$，代入上式得

$v' = \begin {bmatrix}\ 0 \\ 0 \\ 1 \end{bmatrix} \cos\theta + \begin {bmatrix}\ 0& 0 & 1 \end{bmatrix}\begin {bmatrix}\ n_x \\ n_y \\ n_z \end{bmatrix} \begin {bmatrix}\ n_x \\ n_y \\ n_z \end{bmatrix} (1 - \cos \theta) + \begin {bmatrix}\ 0 \\ 0 \\ 1 \end{bmatrix} \times \begin {bmatrix}\ n_x \\ n_y \\ n_z \end{bmatrix} \sin \theta$

$= \begin {bmatrix}\ 0 \\ 0 \\ \cos\theta \end{bmatrix} + \begin {bmatrix}\ n_xn_z \\ n_yn_z \\ n_z^2\end{bmatrix} (1 - \cos \theta) + \begin {bmatrix}\ -n_y \\ n_x \\ 0 \end{bmatrix} \sin \theta$

$= \begin {bmatrix}\ n_xn_z(1-\cos\theta) - n_y\sin\theta \\ n_yn_z(1-\cos\theta) +n_x\sin\theta \\ n_z^2(1-\cos\theta) + \cos\theta \end{bmatrix}$

所以，旋转矩阵

$M_R = \begin {bmatrix}\ n_x^2(1-\cos\theta) + \cos\theta & n_xn_z(1-\cos\theta) + n_z\sin\theta & n_xn_z(1-\cos\theta) - n_y\sin\theta \\ n_xny_(1-\cos\theta) -n_z\sin\theta & n_y^2(1-\cos\theta) + \cos\theta & n_yn_z(1-\cos\theta) +n_x\sin\theta \\ n_xn_z(1-\cos\theta) + n_y\sin\theta & n_yn_z(1-\cos\theta) -n_x \sin\theta & n_z^2(1-\cos\theta) + \cos\theta \end{bmatrix}$

参考

• zhuanlan.zhihu.com/p/56587491