理解法线贴图、切线空间、凹凸贴图

法线能用来做什么？#

考虑这样一面墙，砖块的表面非常粗糙，显然不是完全平坦的：它包含着接缝处水泥凹痕，以及非常多细小的空洞。下图中我们可以看到砖块纹理应用到了平坦的表面，并被一个点光源照亮。

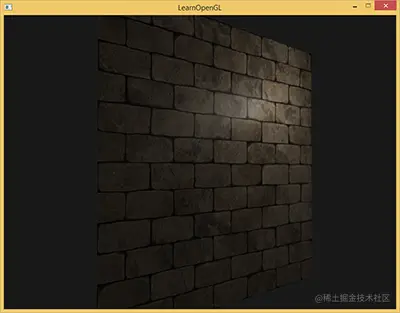
可以看到渲染效果非常不真实，因为光照没有呈现出任何裂痕和孔洞，完全忽略了砖块之前的线条。

从物理上分析，想呈现出真实的效果，需要建立正确的网格，把接缝、孔洞和线条都用三角面建模出来。但这样会需要大量的三角形面，制作工艺和性能不可接受。

那我们可以用一些trick的方法，去模拟真实的情况。真实的墙面，相对于一个建模的平面，差别是

面上的点有高度差。在渲染中，面上的点有高度差，近似于法线不同。

每个点用不同的法线光照后，就可以得到近似真实的接缝、孔洞和线条效果。

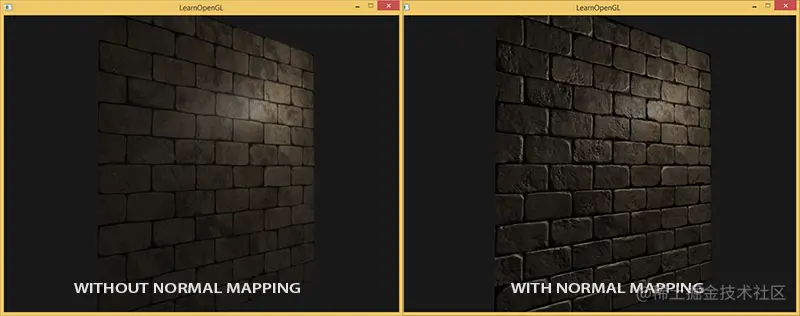
从下图可以看出，用法线贴图控制法线，可以模拟出非常精细的模型渲染出来的光影效果。

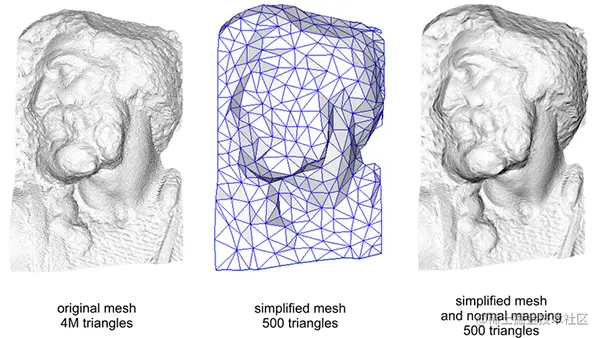
法线如何存储？#

从上一节知道法线对提升效果有很大的帮助，那么法线效果应该存在哪里呢？

存在模型上？肯定不行，因为模型顶点很少，像素很多，顶点法线无法表示像素级别的法线变化。

那就只能存在贴图上了。

法线的数值范围是[-1, 1]，而贴图里不方便存储小于0的值，所以把法线的范围映射到[0, 1]，在shader中采样贴图的时候再映射到[-1, 1]：

storage = normal * 0.5 + 0.5

normal = texture2D(storage) * 2.0 - 1.0

法线的范围我们知道怎么映射了，我们应该存储什么值呢？

考虑到光照计算一般发生在世界空间中，如果我们将在世界空间中的法线值存到贴图中，当模型出现位移/旋转时，法线就会失效。

可以将模型空间的法线存储到贴图中，那么模型发生位移、旋转、缩放时法线也能正常工作。但是当模型发生形变时（骨骼动画） ，这种法线与模型的表面也不再一致，将会出现错误的渲染效果。

考虑以上的旋转、位移、缩放、形变的各种出问题的情况，我们可以根据三角面建立一个空间，把这个空间下的法线存储到贴图中。这个如何理解呢？

模型的三角形面能确定一个法线，根据这个法线再构建出另外两个基向量，就可以组成一个坐标空间，法线贴图中存储各个点的法线在这个空间下的向量，这样的话法线就只跟表面有关系了。在使用贴图的法线前，构建出这个表面空间相对于模型或世界中的变换矩阵，然后把法线变换到模型或世界空间中，就可以进行光照计算了。这个空间称为纹理空间（texture-space） 或切线空间（tangent-space） 。

那么如何构建这个矩阵呢？

考虑一个模型的一个三角面$P_1P_2P_3$，三个点的坐标分别为

$(x_1, y_1, z_1)，(x2, y_2, z_2)，(x_3, y_3, z_3)$

通过向量叉乘很容易求出来模型空间下的法线$\vec{n}$。

现在我们只需要再求出另外两个基向量就可以构造切线空间。

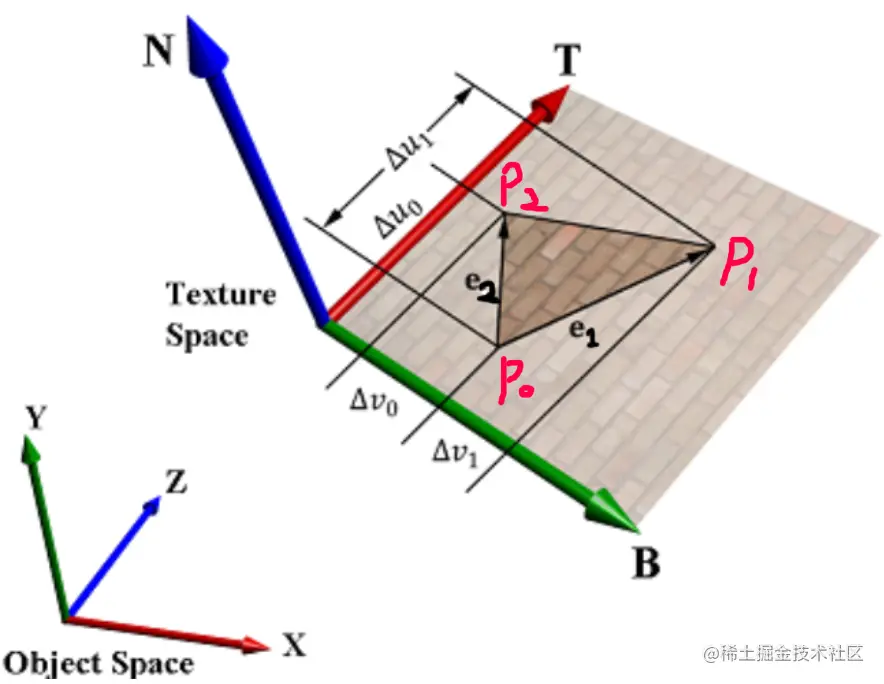
为了方便计算，我们定义模型的切线（tangent）和副切线（bitangent），分别与纹理空间的u和v的方向相同，用向量$\vec{t}$和$\vec{b}$表示 。

三个顶点的纹理坐标为分别是

$(u_1, v_1), (u_2, v_2), (u_3, v_3)$

，将三角形两条边$\overrightarrow{e_1}$和$\overrightarrow{e_2}$与基向量的关系写出来，

$\overrightarrow{e_1} = \Delta{u_0}\overrightarrow{t} + \Delta{v_0}\overrightarrow{b}$

$\overrightarrow{e_2} = \Delta{u_1}\overrightarrow{t} + \Delta{v_1}\overrightarrow{b}$

求$\vec{t}$和$\vec{b}$，把上面的式子写成矩阵形式。

$\begin{bmatrix} \overrightarrow{e_1} & \overrightarrow{e_2} \end{bmatrix} = \begin{bmatrix} \overrightarrow{t} & \overrightarrow{b} \end{bmatrix}\begin{bmatrix} \Delta{u_0} & \Delta{u_1} \\ \Delta{v_0} & \Delta{v_1}\end{bmatrix}$

所以，

$\begin{bmatrix} \overrightarrow{t} & \overrightarrow{b} \end{bmatrix} = \begin{bmatrix} \overrightarrow{e_1} & \overrightarrow{e_2} \end{bmatrix} \begin{bmatrix} \Delta{u_0} & \Delta{u_1} \\ \Delta{v_0} & \Delta{v_1}\end{bmatrix}^{-1}$，即

$\begin{bmatrix} t_x & b_x \\ t_y & b_y \\ t_z & b_z \end{bmatrix} = \begin{bmatrix} e_{1x} & e_{2x} \\ e_{1y} & e_{2y} \\ e_{1z} & e_{2z} \end{bmatrix} \begin{bmatrix} \Delta{u_0} & \Delta{u_1} \\ \Delta{v_0} & \Delta{v_1}\end{bmatrix}^{-1}$

右边的值都是已知的，即可求得$\vec{t}$和$\vec{b}$。

$\vec{t}$和$\vec{b}$不一定是垂直的，尤其在一个顶点被三个面拥有，需要平均这个顶点所在的三个面的法线、切线、副切线时。这时需要用到施密特正交化，将$\vec{t}$、$\vec{b}$和$\vec{n}$变为相互正交的基向量。进行施密特正交化后，新的基向量为

$t' = normalize(t - (t·n)n)$

$b' = normalize(b - (b·n)n - (b·t')t')$

最后组成正交的TBN矩阵，

$\begin{bmatrix} t'_x & b'_x & n_x \\ t'_y & b'_y & n_y \\ t'_z & b'_z & n_z\end{bmatrix}$

这就是法线所需要转换将其到模型空间的矩阵，如果需要转换到世界空间，再乘以模型到世界的矩阵即可。

由于这三个向量相互正交，可以通过其中的两个向量求得另外一个向量，所以一般在顶点中存储将$\vec{t}$和$\vec{n}$，$\vec{b}$由$\vec{n}$和$\vec{t}$的叉乘得到。

法线贴图（normal mapping）#

法线贴图用来存储表面的法线方向，由上面讲述的知识可知，存储在切线空间中的法线比较实用。如果法线方向没有变动，它的值是(0, 0, 1)。由于法线方向一般不会大浮动变动，只是在z轴附近扰动，我们看到的法线贴图一般都呈蓝色。

在shader里采样法线贴图转换为法线后，再乘以TBN矩阵，就可以将法线变换到模型空间，再变换到世界空间就可以进行光照计算了。

凹凸贴图（bump mapping）#

凹凸贴图也是作用在法线上，只不过它存储的不是法线信息，而是存储面上某个点的相对三角面的高度。高度不同，法线自然也不同，也能渲染出模型的凹凸不平的视觉效果。

所以只需要根据相对高度计算出法线信息，之后就可以用TBN矩阵进行后续的光照计算了。

那么如何根据高度信息计算法线呢？

先考虑一维的情况，黄色的线是相对于表面的高度，原表面的法线为垂直于uv方向，在一维中就是(0, 1)，所以已知p的高度，求点p的法线。

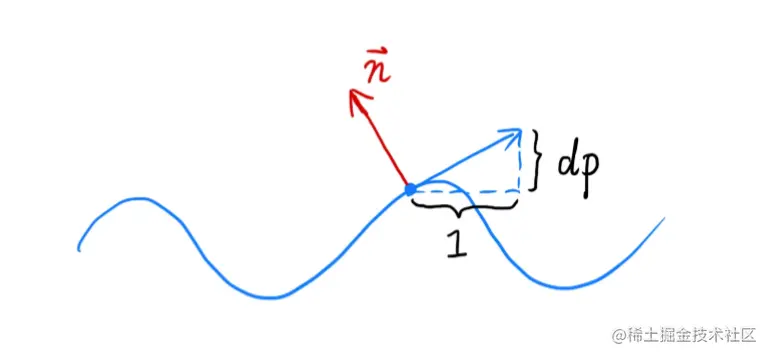
我们先求点p的切线，看上面的图，竖直方向是高度h，水平方向是uv中的u，二者单位不一样，没法直接求切线。所以再引入一个常量s，它表示凹凸贴图的最大高度相对于像素宽度的倍数，有

$dp = \frac{(h(u+1) - h (u))}{\frac{1}{s}} = s(h(u + 1) - h (u))$

所以，切线方向为

$\vec{t} = (1, dp)$

法线为

$\vec{n} = normalize(-dp, 1)$

同理在3维情况下可以得到

$dp/du = s_1(h(u+1, v) - h(u,v))$

$dp/dv = s2(h(u, v + 1) - h(u, v))$

所以，在u方向的切线为

$\vec{t_u} = (1, 0, dp/du)$

在v方向的切线为

$\vec{t_v} = (0, 1, dp/du)$

所求法线为二者的叉乘

$\vec{n} = normalize(cross(\vec{t_u}, \vec{t_v})) = normalize(-dp/du, -dp/dv, 1)$

之后按照切线空间的法线流程计算光照就可以了。

参考#

1. The Cg Tutorial - Chapter 8. Bump Mapping
2. foundationsofgameenginedev.com/FGED2-sampl…
3. sites.cs.ucsb.edu/~lingqi/tea…
4. 法线贴图 - LearnOpenGL CN
5. 计算机图形学八:纹理映射的应用(法线贴图，凹凸贴图与阴影贴图等相关应用的原理详解)_吃人的博客-CSDN博客_纹理映射原理