KCF中的循环矩阵

在学习KCF目标跟踪算法时，会用到一个数学概念：循环矩阵，其对KCF的速度提升起到了非常关键的作用，值得了解下。

1. 傅里叶矩阵(DFT Matrix)

　在了解循环矩阵的定义前，需要先了解下离散傅里叶矩阵：

2. 循环矩阵定义

形状如下的矩阵\(X\)称为循环矩阵，\(x\)为循环矩阵\(X\)的生成向量，为矩阵第一行, 其他行都是\(x\)向右循环位移得到。

\[X=C(x) = \begin{bmatrix} x_1 &x_2 &x_3 &x_4\\ x_4 &x_1 &x_2 &x_3\\ x_3 &x_4 &x_1 &x_2\\ x_2 &x_3 &x_4 &x_1\\ \end{bmatrix} \]

通过\(x\)生成\(X\), 可以由排列矩阵和\(x\)相乘，连续平移\(x\)得到，示例代码如下：

import numpy as np
x = np.array(
    [[1, 2, 3, 4]]
)
P = np.array(
    [[0, 0, 0, 1],
     [1, 0, 0, 0],
     [0, 1, 0, 0],
     [0, 0, 1, 0]]
)
X = np.zeros((4, 4))
X[0, :] = x
for i in range(1, 4):
    X[i, :] = np.dot(P, X[i-1, :]).T  # 排列矩阵P每作用一次x，x向右移动一位
print(X)

输出：
[[1. 2. 3. 4.]
 [4. 1. 2. 3.]
 [3. 4. 1. 2.]
 [2. 3. 4. 1.]]

3. 循环矩阵性质

循环矩阵很多优秀的性质，其中最重要的几个性质为如下：

1. 任意循环矩阵可以被傅里叶变换矩阵对角化

一般用如下方式表达这一概念：

\[X=C(x)=F\cdot diag(\widehat{x})\cdot F^{H} \]

其中\(X\)是一个循环矩阵，\(x\)是\(X\)的生成向量, \(\hat x\)（读作x hat）为原向量\(x\)的傅里叶变换；\(F\)是傅里叶变换矩阵，\(F^H\)表示共轭转置: \(F^H=(F^*)^T\)。换句话说，\(X\)相似于对角阵，\(X\)的特征值是\(\hat x\) 的元素。
另一方面，如果一个矩阵能够表示成两个傅里叶矩阵夹一个对角阵的乘积形式，则它是一个循环矩阵。其生成向量是对角元素的傅里叶逆变换：

\[F\cdot diag({y})\cdot F^{H} = C(\mathcal{F}^{-1}(y)) ，（\mathcal{F}^{-1}(y)表示y的傅里叶逆变换） \]

2. 循环矩阵乘向量等价于生成向量的逆序和该向量卷积

数学表示如下：

\[\mathcal{F}(Xy) = \mathcal{F}(C(x)y) = \mathcal{F}(\bar x*y) = \mathcal{F}^*(x)\odot\mathcal{F}(y) \]

这里\(\bar x\)表示\(x\)的逆序排列，∗表示卷积。

注意：卷积本身也包含逆序操作。此外，这里最后一个等号利用了信号与系统中的“时域卷积，频域相乘”，即时域卷积定理，它表明两信号在时域的卷积积分对应于在频域中该两信号的傅里叶变换的乘积。

3. 循环矩阵的乘积仍是循环矩阵，可以以较低的复杂度计算循环矩阵的乘积

数学表示如下：

\[X^HX = F\cdot diag(\widehat{x}\odot\widehat{x}^*)\cdot F^{H}=C(\mathcal{F}^{-1}(\widehat{x}\odot\widehat{x}^*)) \]

公式中最终所得的乘积也是循环矩阵，其生成向量是原生成向量对位相乘的傅里叶逆变换。

以K表示的是矩阵的尺寸，可以发现计算速度提升非常明显， KCF主要就是利用了这条性质：

• 原始计算量：两个方阵相乘\(O(K^3)\)

• 转化后的计算量：反向傅里叶\(O(Klog(K))\)+向量点乘（\(K\)）

在非线形的情况下，当引入了核之后，也可以得到同样的一个情况。此时需要这个核满足一定的条件，它是可以具备循环矩阵的一些性质的，例如常用的高斯核、线性核都满足这个条件，因此可以直接拿来用。

4. KCF中的循环矩阵

关于KCF的理论推导有很多文章描述了，请参考：

https://blog.csdn.net/shenxiaolu1984/article/details/50905283

https://blog.csdn.net/weixin_38128100/article/details/95729653

https://zhuanlan.zhihu.com/p/48249974

https://gsy00517.github.io/computer-vision20200120120823/

4.1核矩阵K是循环矩阵

在上述KCF的理论推导中有一个前提：即下面表达式中的核矩阵K是循环矩阵

\[优化函数最优解：\alpha=(\phi(X)^T\phi(X)+\lambda I)^{-1}y=(K+\lambda I)^{-1}y \]

这个前提条件是怎么来的呢？满足什么条件时K是循环矩阵呢？

K为核矩阵，其形式如下：（若\(X\)为nxm的矩阵，表示有n条数据，每一条数据的维度为m, 那么对应的核矩阵为nxn的矩阵，每一个元素表示两条数据的内积）

\[核矩阵K = \begin{bmatrix} k(x_1,x_1) & k(x_1,x_2) & \dots & k(x_1,x_n) \\ k(x_2,x_1) & k(x_2,x_2) & \dots & k(x_2,x_n) \\ \vdots &\vdots & &\vdots\\ k(x_n,x_1) & k(x_n,x_2) & \dots & k(x_n,x_n) \end{bmatrix}=\begin{bmatrix} \phi(x_1)\phi(x_1) & \phi(x_1)\phi(x_2) & \dots & \phi(x_1)\phi(x_n) \\ \phi(x_2)\phi(x_1) & \phi(x_2)\phi(x_2) & \dots & \phi(x_2)\phi(x_n) \\ \vdots &\vdots & &\vdots\\ \phi(x_n)\phi(x_1) & \phi(x_n)\phi(x_2) & \dots & \phi(x_n)\phi(x_n) \end{bmatrix} = \phi(X)\phi(X)^T \]

K为循环矩阵的条件就是X为循环矩阵，通过循环矩阵的几条性质可以得到：

• 循环矩阵的转置是循环矩阵: 若\(X\)是循环矩阵，\(X^T\)也是循环矩阵
• 循环矩阵乘以循环矩阵，还是循环矩阵:\(X\)和 \(X^T\)都是循环矩阵，则\(XX^T\)也是循环矩阵
• 相比于\(XX^T\)，\(\phi(X)\phi(X)^T\)多了一层核函数，但对于满足一定条件的核函数，高斯核，多项式核，对应的矩阵仍然是循环矩阵

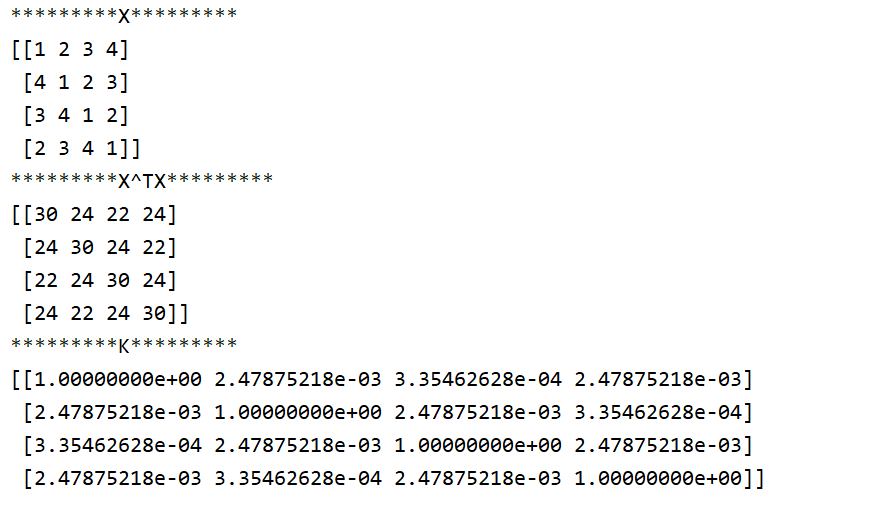
我们可以举个例子验证下，测试代码和结果如下：

def GaussianKernel(X, Y, gamma=1.0):
    n = X.shape[0]
    ret = np.zeros((n, n))
    for i in range(n):
        for j in range(n):
            ret[i,j] = np.sum(np.power((X[i, :] - Y[:, j].T), 2))
    ret = np.exp(ret/(-2*gamma*gamma))
    return ret
    
def recycle_matrix():
    X = np.array(
        [[1, 2, 3, 4],
         [4, 1, 2, 3],
         [3, 4, 1, 2],
         [2, 3, 4, 1]]
    )
    print("*********X*********")
    print(X)

    print("*********X^TX*********")
    print(np.dot(X, X.T))

    print("*********K*********")
    K = GaussianKernel(X, X.T)
    print(K)

    # 调用sklearn中的高斯核函数
    # from sklearn.gaussian_process.kernels import RBF
    # kernel = RBF()
    # K = kernel(X, X.T)
    # print(K)
if __name__ == "__main__":
    recycle_matrix()

4.2 样本X是循环矩阵

上面已经得到：样本\(X\)是循环矩阵，则核矩阵\(K\)是循环矩阵的。那么\(X\)怎样才能成为循环矩阵呢？论文中描述如下：

一维样本构成循环矩阵

论文中，作者先用一维样本举例，如下图所示，循环矩阵的生成向量(base sample)是一个一维的向量(1*m)，这个向量向右循环移动n-1次，生成n-1个向量，所有向量组成一个nxm的循环矩阵

二维样本构成循环矩阵

论文接下来以二维样本为例，如下图所示，循环矩阵的生成向量是一张二维图片(假设为m*m)，每移动一次就会生成一个mxm的矩阵，所有这些mxm的矩阵最后拼接起来组成一个大的循环矩阵，下面是其移动示例过程：

这里是一个循环图片的示例，使用base sample，若我们向下移动15个像素，也就是从下面剪切15个像素拼到上面，就会变成左二图，若移动30个就可以生成左一图，右侧的图片是上移生成的。这就是在做tracking时循环采样的样本，一般会在目标周围取一个比目标更大的一个框，然后对大框框取的图像区域进行循环采样，那么就会生成这样一些新的样本来模拟我们的正样本并用于训练

参考：https://blog.csdn.net/shenxiaolu1984/article/details/50884830