wqs二分学习笔记

其实早就学过了(

但是退役太久又忘了

再学一次.jpg

wqs二分能做什么？

从$n$个物品中，恰选出$m$个，问你最优方案。

拿个例题来说吧。

例题：

Luogu P4893 忘情

link:

https://www.luogu.com.cn/problem/P4983

首先这个式子就一副欠收拾的样子==

考虑把$\sum x_i$先转化成$len * \overline{x} $

然后扔进去算，消去一下$\overline{x}$，再把$len * \overline{x}$展开为$\sum x_i$

就会发现其实每个子段的贡献其实是$(\sum {x_i}+1)^2 $

那么我们就可以得到一个native的$dp$

$dp_{i,j}=min(dp_{k,j-1}+ (sum_j - sum_{i-1} +1)^2)$

正常跑是$O(n^2m)$的，如果你会斜率优化能优化到$O(nm)$，但还是寄了(

这时候$wqs$二分就可以派上用场了。

在用$wqs$二分之前，我们先考虑一个性质:

随着分的段数的增长，$f(x)$一定是下降的，而且是一个下凸函数

因为$(x+y)^2$>$x^2 + y^2$

于是其实，分的段数越多，显然贡献是下降的

那么为什么下凸呢？

考虑划分的时候丢掉了什么，暂时只考虑两个元素的划分

丢掉的是$2xy$，而题目希望求这个函数的最小值，于是我们感性理解一下，一定会从$2xy$大的地方划到$2xy$小的地方

也就是说，其实这个划分过程，答案函数的下降速度是在放缓的

对应到图像上的性质就是这个函数下凸

于是我们考虑凸包上的答案。

 

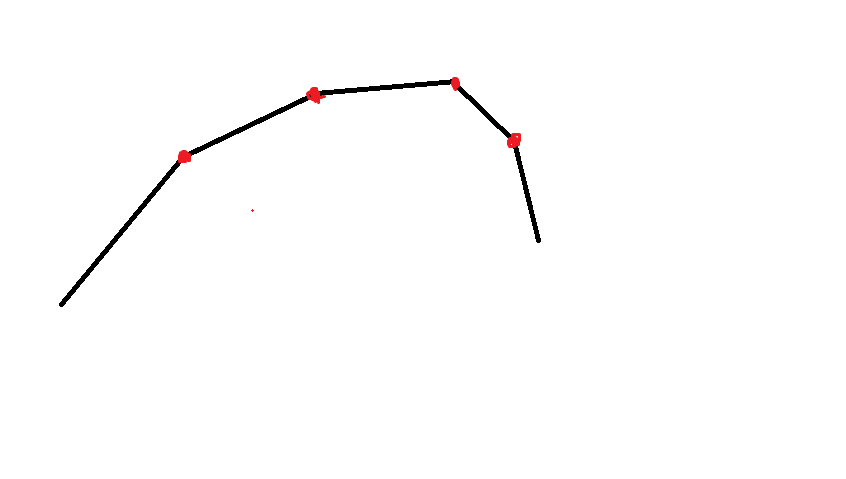
 凸包大概长这样(

现在考虑用一个已知斜率的直线去切凸包

容易发现的是，当这个直线的截距最大的时候，一定是和这个凸包相切在关键点的时候

 

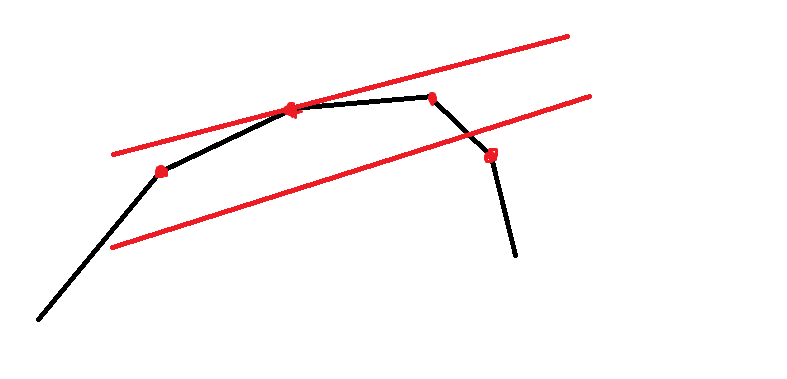
 而我们把答案函数抽象成$(x,f(x))$这样的点，就会有$f(x)=k*x+b$,$b=f(x)-k*x$

$b$就是最大化$f(x)-k*x$的时候。

因为$f(x)$是划分的结果，其实我们只需要把每次划分的时候的代价加上$k$作为权重就可以了(把$k*x$分配进每一次划分里)

这时候我们通过相同$dp$,可以计算出当前划分的段数。也就是式子里的$x$

如果$x$在我需要的段数左侧，对于这个图来说，就说明斜率要减小，往右侧找。

反之同理。

于是最后我们一定能卡到这个答案的点，输出即可。

具体的说，考虑这个题。

我当前二分出了一个斜率$mid$，要怎么算$x$?

其实就是给每次划分加一个权值$mid$，考虑最后划分的段数与需要的段数的大小关系

少了往左找，多了往右找。

$dp_i = min(dp_j,dp_k + (sum_i - sum_{k-1} +1)^2$

$g_i = g_k +1$

这个显然是可以斜率优化成$O(n)$

Code:

#include<bits/stdc++.h>
using namespace std;
int N,M;
long long ans,x[100005],Sum[100005],dp[100005],g[100005];
int que[100005];
long long Getx(int pos){
    return Sum[pos];
}
long long Gety(int pos){
    return dp[pos]+Sum[pos]*Sum[pos]-2ll*Sum[pos];
}
bool Check(long long mid){
    for (int i=1;i<=N;i++)
        dp[i]=1e18,g[i]=0;
    int head=1,tail=1;
    que[1]=0;
    for (int i=1;i<=N;i++){
        while (head<tail && 2ll*Sum[i]*(Getx(que[head+1])-Getx(que[head])) > (Gety(que[head+1])-Gety(que[head]))) head++;
        dp[i]=dp[que[head]]+((Sum[i]-Sum[que[head]]+1)*(Sum[i]-Sum[que[head]]+1)+mid);
        g[i]=g[que[head]]+1;
        while (head<tail && (Gety(que[tail])-Gety(que[tail-1]))*(Getx(i)-Getx(que[tail-1])) > (Gety(i)-Gety(que[tail-1]))*(Getx(que[tail])-Getx(que[tail-1])))
            tail--;
        que[++tail]=i;
    }
    if (g[N]<=M) return true;
    else return false;
}
int main(){
    scanf("%d%d",&N,&M);
    for (int i=1;i<=N;i++){
        scanf("%lld",&x[i]);
        Sum[i]=Sum[i-1]+x[i];
    }
    long long l=0,r=1e18;
    while (l<=r){
        long long mid=(l+r)>>1; 
        if (Check(mid)) r=mid-1,ans=mid;
        else l=mid+1;
    }
    Check(ans);
    printf("%lld\n",dp[N]-M*ans);
}