插头dp

　　众所周知，shzr不擅长dp，所以她决定多学几个算法来提高（看上去的）知识水平。

　　插头dp：基于连通性的状态压缩动态规划；

　　接下来以这道例题：[模板]插头dp 来学习插头dp;

[模板]插头dp

题意概述

 

状态设计

　　插头是什么呢？插头就是表示一个格子上是否有未结束的路径的一种方法（有的话就可以继续延伸）；

　　每个格子可能存在六种插头：上下，左右，上左，上右，下左，下右；6种感觉太复杂了，我们对其进一步转化，每次只考虑一条分割线上的插头，那么就只需要考虑每个位置是否有插头了；

　　因为状态比较复杂，考虑一格一格地转移，具体做法是状压轮廓线；

　　注意：状压的是轮廓线（图左）而不是轮廓上的格子（图右）；

　　

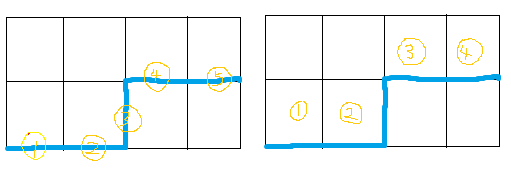
　　所以每个状态应该包含m+1位而不是m位；

　　因为需要最后连成一个回路，所以需要记录插头的联通性。可以发现，如果轮廓线上依次存在abcd四个插头，那不可能出现ac联通，bd联通，而ab之间却不联通的情况，这与括号匹配有一点相似；所以我们对于每个插头分配一个括号来表示轮廓线上的联通性。当然...有些线上可能并没有插头，所以还需要再一种状态表示。那么，每段轮廓线就有三种状态：左括号，右括号，无括号；因为位运算比较快，我们用四进制状压表示这个状态；这样有一个小小的坏处，就是很多状态根本不存在，所以可以考虑将所有存在的状态进行Hash，每次只用这些状态进行转移；

　　现在，我们就得到了这道题的dp状态设计：dp[i][j][k]表示当前dp完了前i-1行以及第i行的前j个格子，轮廓线状态为k的方案数；

 

转移

　　转移情况有点多，下面会一一列举：

　　1.当前位置有障碍：如果这个格子的左边上边都没有插头，那么轮廓线状态不变，否则不能转移；（以下情况均默认当前格子无障碍）

　　2.左边上边都没有插头：可以考虑新建一个连通分量，也就是在当前格子加入右插头，下插头；同时，由于他们是联通的，所以直接加入一对括号；

　　3.左边有插头，上边没有；可以考虑向右延续插头，也可以拐弯向下；

　　4.上边有插头，左边没有；可以考虑向下延续插头，也可以拐弯向右；

　　上边左边都有插头的话，又分为多种情况：

　　5.都是左括号：这个比较有趣，可以发现，我们将j-1,j两个插头连接后，原本与j配对的右插头，由于和j-1这个左插头连着...变成左插头了！所以可以通过一个O(M)的循环找到这个右括号并进行更改；

　　6.都是右括号：和上面那种差别不大吧；

　　7.“)(”：在这里连一下，恰好联通了两个连通分量！不过呢，别忘了连接后这里就没插头了，要把这对括号一起删掉；

　　8.“()”：已经连通了！也就是说如果这里连一下的话，就形成回路了。所以要注意，如果当前格子不是最后一个空格的话，这个状态就不能转移，否则直接加进最终答案里；

 

实现技巧 

　　假设我们当前考虑的格子是(i,j)，那么在轮廓线上，可以通过:

　　

　　来得到当前格子左边和上边的轮廓线情况；

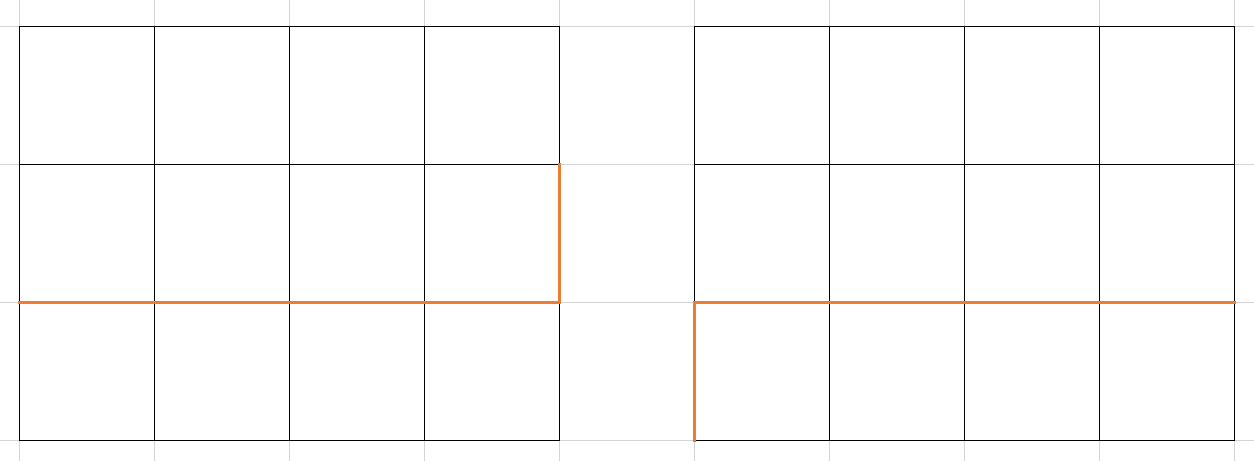
　　一个要特殊考虑的情况是：换行时，需要把之前的所有状态左移两位，也就是舍弃最后一段轮廓线，在前面加一段无插头的轮廓线。这是为什么呢？这里有一张图来解释：（换行后，考虑的轮廓线从左边这样变成了右边这样）

　　

 

代码

　　 
  1 # include <cstdio>
  2 # include <iostream>
  3 # include <algorithm>
  4 # include <queue>
  5 # include <map>
  6 # include <vector>
  7 # include <cmath>
  8 # include <cstring>
  9 # define R register int
 10 # define ll long long
 11 
 12 using namespace std;
 13 
 14 const int N=13;
 15 const int Q=540005;
 16 const int base=299989;
 17 int n,m,a[N][N],no=0,las=1,tx,ty;
 18 int bit[N],cnt[2],nex[Q],h[Q],t[2][Q];
 19 char s[N];
 20 ll ans,v[2][Q];
 21 //t[no][x]:x代表的真实状态;
 22 //v[no][x]:x代表的真实状态的dp值；
 23 
 24 void Hash (int id,ll val)
 25 {
 26     int x=id%base;
 27     for (R i=h[x];i;i=nex[i])
 28         if(t[no][i]==id) { v[no][i]+=val; return; }
 29     cnt[no]++; 
 30     nex[ cnt[no] ]=h[x]; h[x]=cnt[no];
 31     t[no][ cnt[no] ]=id; v[no][ cnt[no] ]=val;
 32 }
 33 
 34 int main()
 35 {
 36     scanf("%d%d",&n,&m);
 37     for (R i=1;i<=n;++i)
 38     {
 39         scanf("%s",s+1);
 40         for (R j=1;j<=m;++j)
 41         {
 42             if(s[j]=='*') continue;
 43             a[i][j]=1,tx=i,ty=j;
 44         }
 45     }
 46     bit[0]=1; for (R i=1;i<=m;++i) bit[i]=bit[i-1]<<2;
 47     cnt[no]=1; t[no][1]=0; v[no][1]=1;
 48     for (R i=1;i<=n;++i)
 49     {
 50         for (R k=1;k<=cnt[no];++k) t[no][k]<<=2;
 51         for (R j=1;j<=m;++j)
 52         {
 53             swap(no,las);
 54             memset(h,0,sizeof(h)); cnt[no]=0;
 55             for (R k=1;k<=cnt[las];++k)
 56             {
 57                 int id=t[las][k]; ll val=v[las][k];
 58                 int lef=(id>>(2*(j-1)))%4,up=(id>>(2*j))%4;
 59                 if(!a[i][j])
 60                 {
 61                     if(!lef&&!up) Hash(id,val);
 62                 }
 63                 else if(!lef&&!up)
 64                 {
 65                     if(a[i+1][j]&&a[i][j+1]) 
 66                         Hash(id+bit[j-1]+2*bit[j],val); //新建插头
 67                 }
 68                 else if(!lef&&up)
 69                 {
 70                     if(a[i+1][j]) Hash(id-bit[j]*up+bit[j-1]*up,val);
 71                     if(a[i][j+1]) Hash(id,val); 
 72                 }
 73                 else if(lef&&!up)
 74                 {
 75                     if(a[i+1][j]) Hash(id,val);
 76                     if(a[i][j+1]) Hash(id-bit[j-1]*lef+bit[j]*lef,val);
 77                 }
 78                 else if((lef==1)&&(up==1))
 79                 {
 80                     int s=1;
 81                     for (R k=j+1;k<=m;++k)
 82                     {
 83                         if((id>>(2*k))%4==1) s++;
 84                         if((id>>(2*k))%4==2) s--;
 85                         if(s==0)
 86                         {
 87                             Hash(id-bit[j-1]-bit[j]-bit[k],val);
 88                             break;
 89                         }
 90                     }
 91                 }
 92                 else if((lef==2)&&(up==2))
 93                 {
 94                     int s=1;
 95                     for (R k=j-2;k>=0;--k)
 96                     {
 97                         if((id>>(2*k))%4==1) s--;
 98                         if((id>>(2*k))%4==2) s++;
 99                         if(s==0)
100                         {
101                             Hash(id-2*bit[j-1]-2*bit[j]+bit[k],val);
102                             break;
103                         }
104                     }
105                 }
106                 else if((lef==2)&&(up==1))
107                 {
108                     Hash(id-lef*bit[j-1]-up*bit[j],val);
109                 }
110                 else if((lef==1)&&(up==2))
111                 {
112                     if(i==tx&&j==ty) ans+=val;
113                 }
114             }
115         }
116     }
117     printf("%lld",ans);
118     return 0;
119 }
插头dp

 

[HNOI2007]神奇游乐园

posted @ 2020-04-05 19:41  shzr  阅读(260)  评论(0)    收藏  举报