Skeleton-Based Action Recognition with Directed Graph Neural Network

Skeleton-Based Action Recognition with Directed Graph Neural Network

摘要

因为骨架信息可以鲁棒地适应动态环境和复杂的背景，所以经常被广泛应用在动作识别任务上，现有的方法已经证实骨架中的关键点和骨头信息对动作识别任务非常有用。然而如何将两种类型的数据最大化地利用还没有被很好地解决。

作者将骨架数据表示成一个有向非循环图（Directed acyclic graph），该图基于自然人体的节点和骨骼的动力学依赖。

这个新颖的图结构用来提取节点、骨骼和他们之间的关联信息，然后基于提取到的特征进行预测。

另外，为了更好地适应动作识别任务，图的拓扑结构可以根据训练过程进行自适应地改变，这极大地提高了性能。

此外，利用骨架序列的运动信息与空间信息相结合，进一步提高了双流框架的性能。

算法在NTU-RGBD和Skeleton-Kinetics数据集上的性能远超流行算法。

一、引言

动作识别任务在很多方面都有应用，其中，人体骨架信息有很多优势，比如对尺度变化、背景干扰等具有很强的鲁棒性，而且骨架信息很容易通过硬件设备（kinetics）或者软件（openpose）获得。传统的基于骨架的动作识别通常手动设计特征来表示骨架，现有的基于深度学习的方法分为三种：RNN、CNN、GCN，其中连接点信息分别被表示成向量序列、伪图像、图。骨头信息，表征着人体骨头的方向和长度，它和关节点坐标信息是互补的，骨头和关节点是紧密相连的。（从人体骨骼自然结构说明了构造有向图的必要性）现有的基于图的方法通常把骨骼信息表示成一个无向图，并且用两个网络对骨头和关节点进行建模，这样不能将骨头和关节点之间的依赖关系完全探索出来。因此，作者以关节点为节点、骨头为边设计出了一个有向无环图，还设计了一个有向图卷积网络来对构造的图进行建模，这样提取到的特征不仅包含每个关节点和骨头信息，而且还有他们之间的依赖关系，促进了动作识别。另外一个问题是原始的骨架结构是手动设计的，不能根据动作识别任务进行优化，作者提出了一个自适应的图结构代替原始的固定的图结构，并且使用一个简单有效的方法一方面保证了训练过程的稳定性，另一方面有不失灵活，在性能上带来了显著提升。双流网络给基于RGB的动作识别带来了性能上的提升，作者也采用双流结构将空间流和时间流的结果融合来增强算法性能。

总结

• 据作者所知，他们是第一个用有向无环图来表示关节点和骨头信息以及他们之间的依赖关系
• 自适应的网络结构在训练过程中与模型参数共同训练和更新
• 双流结构
• 在NTU RGB+D和Kinects数据集上效果很好

二、相关工作

1. 基于骨架的动作识别

现有的方法主要分为三类：基于序列的方法、基于图像的方法、基于图的方法。基于序列的方法将骨架信息表示成有着设计好的遍历规则的骨架序列，然后用RNN进行动作识别；基于图像的方法通常把骨架信息表示成伪图像；基于图的方法用图来表示骨架信息，天然地保留了人体骨架信息。

2. 图网络

图结构是比图像和序列更一般化的数据结构，它不能直接用深度学习模块，比如CNN、RNN直接进行建模。用图网络结构来解决问题已经被探索了很多年了。

三、方法

给出一个骨架序列，首先根据节点的2D或3D坐标信息将骨头信息提取出来，然后根据每一帧的节点和骨头信息构建一个有向无环图，然后把它送到有向图卷积中提取特征用来进行动作识别。最后，用和提取空间信息相同的图网络结构提取动作信息，动作信息和空间信息的融合来进一步提高性能。

和2s-AGCN相似，在其基础上改变了网络结构，使用有向无环图构建人体骨架结构，并且改变了自适应网络的方法。

1. 有向图网络结构块

根据有向图结构更新节点和边的信息，更新方式如下：

\[\overline{\mathbf{e}}_{i}^{-}=g^{\mathbf{e}^{-}}\left(\mathcal{E}_{i}^{-}\right) \qquad（1）\\ \overline{\mathbf{e}}_{i}^{+}=g^{\mathbf{e}^{+}}\left(\mathcal{E}_{i}^{+}\right) \qquad（2）\\ \mathbf{v}_{i}^{\prime}=h^{\mathbf{v}}\left(\left[\mathbf{v}_{i}, \overline{\mathbf{e}}_{j}^{-}, \overline{\mathbf{e}}_{j}^{+}\right]\right) \qquad（3）\\ \mathbf{e}_{j}^{\prime}=h^{\mathbf{e}}\left(\left[\mathbf{e}_{j}, {\mathbf{v}}_{j}^{s'}, {\mathbf{v}}_{j}^{t'}\right]\right) \qquad（4） \]

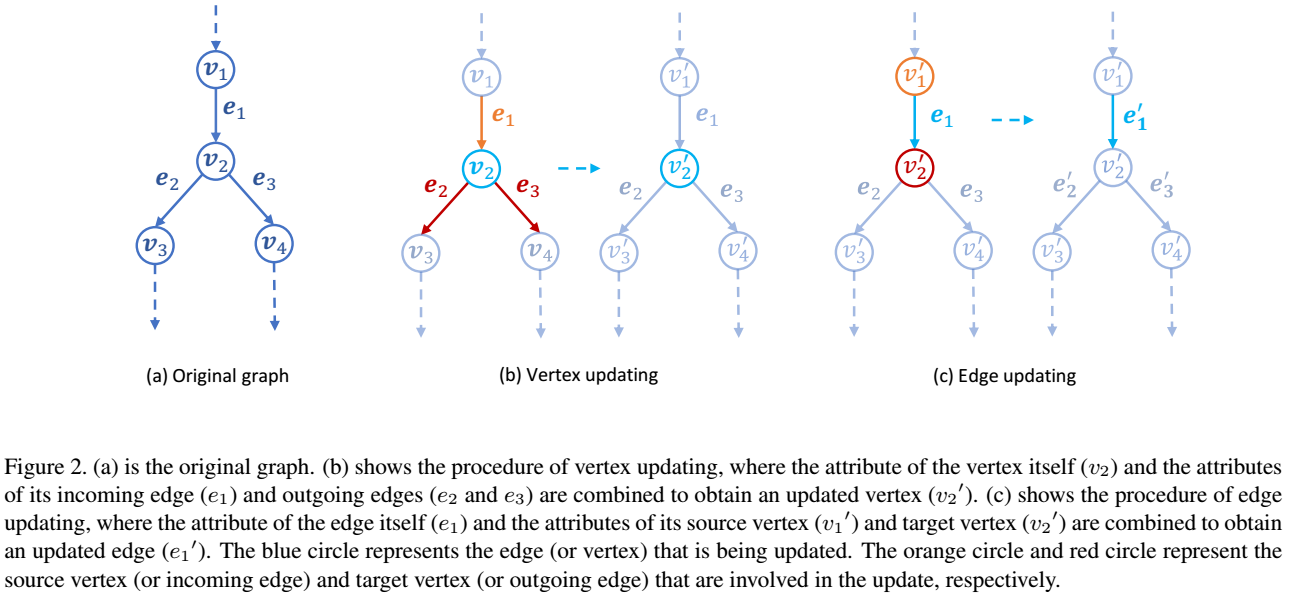
\(e^-\)表示输入边，\(e^+\)表示输出边，对于下图(a)中的节点\(v_2\)，输入边为\(e_1\)，输出边为\(e_2\)和\(e_3\)，\(v^s\)表示源点，\(v^t\)表示目标点，对于下图(a)中的边\(e_1\)，源点为\(v_1\)，目标点为\(v_2\)，函数\(g\)表示聚合函数，函数\(h\)表示更新函数。

对网络中一个DGN块，首先对有向图中的边和节点进行更新，针对\(v_2\)节点，先对输入边和输出边用聚合函数进行聚合（上式中的（1）和（2）），再对\(v_2\)节点进行更新，最后用更新后的\(v^{'}_1\)和\(v^{'}_2\)对边\(e_1\)进行更新。

2.实现

输入：\(f_v\)是节点的特征图，大小为\(C \times T \times N_v\)，并将其resize为\(CT \times N_v\)；

    \(A\)是节点与边的对应关系矩阵，大小为\(N_v \times N_e\)，\(A_{ij}\)表示第i个节点是第j条边源点或目标点，当\(A_{ij}\)为-1时，表示是源点，为1时，表示是目标点，为0时，表示节点和边没有关系。如下图，表示第0个节点是第0条边的源点，第0个节点是第1条边的目标点。为了实施过程简单一些，将\(A\)分为\(A^s\)和\(A^t\)，将源点和目标点分别提取出来形成单独的向量，并将值全设为1；

\[A=\left[\begin{array}{rrrr}{-1} & {1} & {0} & {0} \\ {0} & {-1} & {1} & {0} \\ {0} & {-1} & {0} & {1}\end{array}\right]^{\top}\\ A^s=\left[\begin{array}{rrrr}{1} & {0} & {0} & {0} \\ {0} & {1} & {0} & {0} \\ {0} & {1} & {0} & {0}\end{array}\right]^{\top} \qquad A^t=\left[\begin{array}{rrrr}{0} & {1} & {0} & {0} \\ {0} & {0} & {1} & {0} \\ {0} & {0} & {0} & {1}\end{array}\right]^{\top} \]

将\(f_v\)和\(A^s\)相乘便得到大小为\(CT \times N_e\)的矩阵，表示某个点对应的输入边的聚合，从而实现了聚合函数的功能，因为需要对聚合后的结果进行归一化，等价于直接对\(A\)进行归一化，\(\tilde{A}=A \Lambda^{-1}\)，$ \Lambda_{ii} = \sum_jA_{ij}+\epsilon\(，\)\epsilon$是为了避免除零，所以上述更新节点和边可以写成：

\[f^{'}_v = H_v([f_v,f_e\tilde{A^s}^T,f_e\tilde{A^t}^T])\\ f^{'}_e = H_e([f_e,f_v\tilde{A^s}^T,f_v\tilde{A^t}^T]) \]

\(H\)表示一个全连接层来表示更新函数。

3.自适应图结构

\(A\)：指的是邻接矩阵的形式

\(A_0\)：自然人体骨架结构图

\(A = PA_0\)：ST-GCN的实现方式，这种方法只能改变已经存在的边的重要性，不能生成新的边

\(A = A_0 + P\)：这种方式可以生成新的边，但是无法移除原有的不需要的边

\(A = P\)：这种方法会使得图结构的学习不收任何约束，反而会降低性能

\(A = P_{10}\)：表示 前10次迭代\(A = A_0\)，后面的迭代\(A = P\)，这样用固定的图结构使得前期更容易训练，后期的 不固定的图结构带来了更多的灵活性。

4.时域信息建模

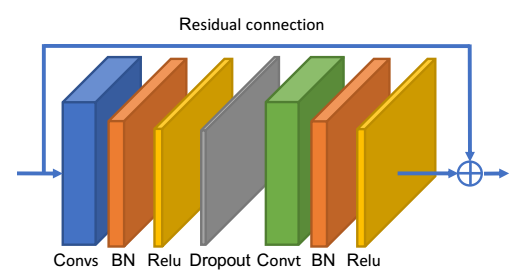
与ST-GCN相同，2s-AGCN和DGN的每个GCN（DGN）块都有一个TCN块，用\(K_t \times 1\)对时间域进行卷积。结构与2s-AGCN中的结构完全相同，就是把Convs替换成DGN块。

5.双流结构

双流结构与2s-GCN相同，都是利用骨骼长度和方向信息作为第二类信息，和节点信息组成双流结构，最后用加和进行融合产生最后的打分值。

四、实验结果

1.消融实验

2s-ST-GCN表示节点和骨头信息双流结构应用在ST-GCN上

1s-ST-GCN表示节点和骨头信息合为一流结构应用在ST-GCN上

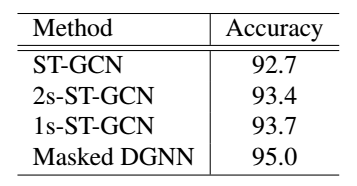
2.自适应的DGN

3.双流网络对比

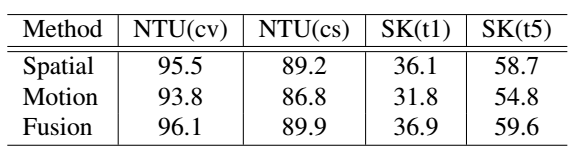
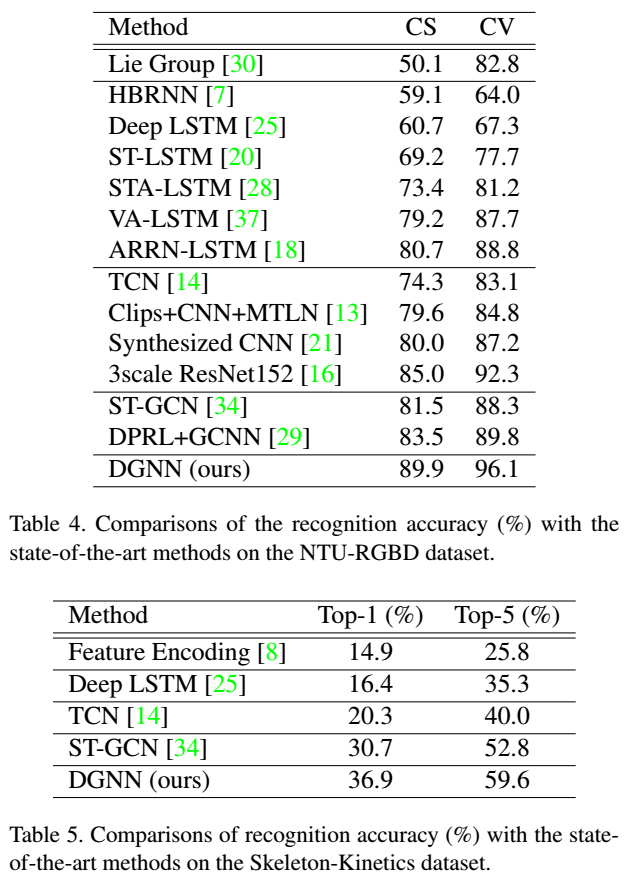
4.和state-of-the-art对比

原文链接：原文链接
代码链接：代码链接

版权声明：本文为博主原创文章，未经博主允许不得转载。

出处：https://www.cnblogs.com/shyern/