图解AI数学基础 | 信息论

• 作者：韩信子@ShowMeAI
• 教程地址：https://www.showmeai.tech/tutorials/83
• 本文地址：https://www.showmeai.tech/article-detail/164
• 声明：版权所有，转载请联系平台与作者并注明出处

---

信息论是运用概率论与数理统计的方法研究信息、信息熵、通信系统、数据传输、密码学、数据压缩等问题的应用数学学科。信息论中包含的知识和概念在机器学习中也有应用，典型的例子是其核心思想『熵』的应用。

例如，决策树模型ID3、C4.5中是利用信息增益来确定划分特征而逐步生长和构建决策树的；其中，信息增益就是基于信息论中的熵。

1.熵（Entropy）

熵是1854年由克劳休斯提出的一个用来度量体系混乱程度的单位，并阐述了热力学第二定律熵增原理：在孤立系统中，体系与环境没有能量交换，体系总是自发的向混乱度增大的方向变化，使整个系统的熵值越来越大。

熵越大，表征的随机变量的不确定度越大，其含有的信息量越多。

随机变量 $X$ 可能的取值为 $\{x_{1},x_{2} ,\dots ,x_{n} \}$，其概率分布为$P(X=x_{i}) =p_{i}$，$i = 1, 2, \dots, n$，则随机变量 $X$ 的熵定义为$H(X)$：

$$\begin{aligned} H(X) =&-\sum_{i=1}^{n}{P(x_{i}) logP(x_{i})} \\ &=\sum_{i=1}^{n}{P(x_{i}) \frac{1}{logP(x_{i})}} \end{aligned}$$

2.联合熵（Joint Entropy ）

联合熵，就是度量一个联合分布的随机系统的不确定度。分布为 $P(x,y)$ 的一对随机变量$(X,Y)$，其联合熵定义为：

$$\begin{aligned} H(X,Y) &=-\sum_{i=1}^{n}{\sum_{j=1}^{n}{P(x_{i},y_{j})}logP(x_{i},y_{j})} \\ &=E[ \log\frac{1}{p(x,y)} ] \end{aligned}$$

联合熵的物理意义，是观察一个多随机变量的随机系统获得的信息量，是对二维随机变量$(X,Y)$不确定性的度量。

3.条件熵（Conditional Entropy）

$Y$ 的条件熵是指『在随机变量 $X$ 发生的前提下，随机变量 $Y$ 发生新带来的熵』，用 $H(Y \mid X)$ 表示：

$$H(Y \mid X) =-\sum_{x,y}{P(x,y) logP(y \mid x)}$$

条件熵的物理意义，在得知某一确定信息的基础上获取另外一个信息时所获得的信息量，用来衡量在已知随机变量的 $X$ 条件下，随机变量 $Y$ 的不确定性。

4.相对熵（Kullback–Leibler divergence）

相对熵在信息论中用来描述两个概率分布差异的熵，叫作KL散度、相对熵、互熵、交叉熵、信息增益。对于一个离散随机变量的两个概率分布 $P$ 和 $Q$ 来说，它们的相对熵定义为：

$$D(P \parallel Q) =\sum_{i=1}^{n}{P(x_{i}) log\frac{P(x_{i})}{Q(x_{i})}}$$

注意：公式中 $P$ 表示真实分布，$Q$ 表示 $P$ 的拟合分布，$D(P \parallel Q) ≠ D(Q \parallel P)$。

相对熵表示当用概率分布 $Q$ 来拟合真实分布 $P$ 时，产生的信息损耗。

5.互信息（Mutual Information）

互信息是信息论里一种有用的信息度量方式，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性。

互信息的计算方式定义如下：

$$I(X,Y) =\sum_{x\in X}^{}{\sum_{y\in Y}^{}{P(x,y)} log\frac{P(x,y)}{P(x) P(y)}}$$

6.常用等式（useful equations）

1）条件熵、联合熵与熵之间的关系

$$H(Y \mid X) =H(X,Y) - H(X)$$

推导过程如下：

$$\begin{aligned} H(X, Y)-H(X) &= -\sum_{x, y} p(x, y) \log p(x, y)+\sum_{x} p(x) \log p(x) \quad \quad \text{(1)} \\ &=-\sum_{x, y} p(x, y) \log p(x, y)+\sum_{x}(\sum_{y} p(x, y)) \log p(x) \quad \text{(2)} \\ &=-\sum_{x, y} p(x, y) \log p(x, y)+\sum_{x, y} p(x, y) \log p(x) \quad \quad \text{(3)} \\ &=-\sum_{x, y} p(x, y) \log \frac{p(x, y)}{p(x)} \quad \quad \text{(4)} \\ &=-\sum_{x, y} p(x, y) \log p(y \mid x) \quad \quad \text{(5)} \end{aligned}$$

• 第（1）行推到第（2）行的依据是边缘分布 $P(x)$ 等于联合分布 $P(x,y)$ 的和；

• 第（2）行推到第（3）行的依据是把公因子 $logP(x)$ 乘进去，然后把$x,y$写在一起；

• 第（3）行推到第（4）行的依据是：因为两个 $\sigma$ 都有 $P(x,y)$ ，故提取公因子 $P(x,y)$ 放到外边，然后把里边的 $-(log P(x,y) - log P(x))$ 写成 $- log (P(x,y) / P(x))$；

• 第（4）行推到第（5）行的依据是：$P(x,y) = P(x) \ast P(y \mid x)$，故$P(x,y) / P(x) = P(y \mid x)$。

2）条件熵、联合熵与互信息之间的关系

$$H(Y \mid X) =H(Y) -I(X,Y)$$

推导过程如下：

$$\begin{aligned} H(Y)-I(X, Y) =&-\sum_{y} p(y) \log p(y)-\sum_{x, y} p(x, y) \log \frac{p(x, y)}{p(x) p(y)} \\ &=-\sum_{y}(\sum_{x} p(x, y)) \log p(y)-\sum_{x, y} p(x, y) \log \frac{p(x, y)}{p(x) p(y)} \\ &=-\sum_{x, y} p(x, y) \log p(y)-\sum_{x, y} p(x, y) \log \frac{p(x, y)}{p(x) p(y)} \\ &=-\sum_{x, y} p(x, y) \log \frac{p(x, y)}{p(x)} \\ &=-\sum_{x, y} p(x, y) \log p(y \mid x) \\ &=H(Y \mid X) \end{aligned}$$

3）互信息的定义

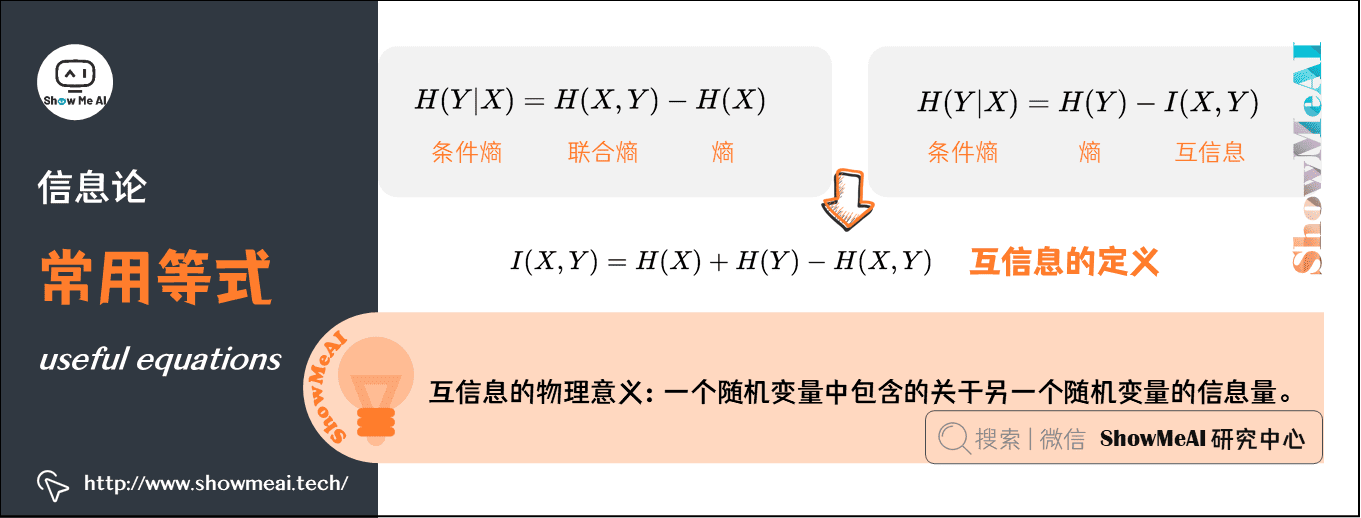
由上方的两个公式

• $H(Y \mid X) = H(Y) - I(X,Y)$
• $H(Y \mid X) = H(X,Y) - H(X)$

可以推出 $I(X,Y)= H(X) + H(Y) - H(X,Y)$，此结论被多数文献作为互信息的定义

7.最大熵模型（Max Entropy Model）

机器学习领域，概率模型学习过程中有一个最大熵原理，即学习概率模型时，在所有可能的概率分布中，熵最大的模型是最好的模型。

通常用约束条件来确定模型的集合，所以最大熵模型原理也可以表述为：在满足约束条件的模型集合中，选取熵最大的模型。

前面我们知道，若随机变量 $X$ 的概率分布是 $P(x_{i})$，其熵的定义如下：

$$H(X) =-\sum_{i=1}^{n}{P(x_{i}) logP(x_{i})} =\sum_{i=1}^{n}{P(x_{i}) \frac{1}{logP(x_{i})}}$$

熵满足下列不等式：$0 \leq H(X) \leq log \left| X \right|$

• $|X|$是 $X$ 的取值个数
• 当且仅当 $X$ 的分布是均匀分布时，右边的等号成立；也就是说，当 $X$ 服从均匀分布时，熵最大。

直观地看，最大熵原理认为：

• 要选择概率模型，首先必须满足已有的事实，即约束条件；
• 在没有更多信息的情况下，那些不确定的部分都是『等可能的』。最大熵原理通过熵的最大化来表示等可能性；『等可能』不易操作，而熵则是一个可优化的指标。

ShowMeAI人工智能数学要点速查（完整版）

• ShowMeAI 图解AI数学基础(1) | 线性代数与矩阵论
• ShowMeAI 图解AI数学基础(2) | 概率与统计
• ShowMeAI 图解AI数学基础(3) | 信息论
• ShowMeAI 图解AI数学基础(4) | 微积分与最优化

ShowMeAI系列教程精选推荐

• 大厂技术实现方案系列
• 图解Python编程：从入门到精通系列教程
• 图解数据分析：从入门到精通系列教程
• 图解AI数学基础：从入门到精通系列教程
• 图解大数据技术：从入门到精通系列教程
• 图解机器学习算法：从入门到精通系列教程
• 机器学习实战：手把手教你玩转机器学习系列
• 深度学习教程：吴恩达专项课程 · 全套笔记解读
• 自然语言处理教程：斯坦福CS224n课程 · 课程带学与全套笔记解读
• 深度学习与计算机视觉教程：斯坦福CS231n · 全套笔记解读