决策树-笔记（1）

1 - 背景

决策树：是基于树结构的一种机器学习方法。其训练方法决定了它是一种有监督学习方法，且和KNN一样是一种非参数化模型。且当类数较多时，该方法具有一定的优势[1]。最流行的决策树是将空间拆分成超矩形，超矩形的边与轴平行。常用的算法有：CHAID、 CART、ID3、C4.5、 Quest 和C5.0（后续慢慢更新）。
ps：参数化模型，有着固定数量的参数，通常在预测阶段速度很快，而缺点就是对数据分布有着先验假设；非参数化模型，其参数会随着训练集的增大而增加，所以相对更加灵活，可是对于大数据集来说，其计算效率相对低下。

树结构主要都是由根节点，内部节点，叶节点组成。根节点：作为树的入口，也作为第一个判别特征点；内部节点：在当得到其父节点的时候，父节点需要接着划分，且自身还需要进一步划分；叶节点，基于父节点划分基础上，分到当前结点的样本无需进一步划分，且叶节点所表示的标签为当前叶节点包含的样本中标签最多的那个标签。
通常会有四种情况：
1）这是一棵空树；
2）这是一棵只有根节点的树；
3）这是一棵只有根节点，叶子节点的树；
4）这是一棵具有根节点、内部节点、叶子节点的完整树。
情况1）：此时对应的是训练数据集为空,或者未开始训练；
情况2）：此时训练集都被归为同一个类别，比如训练集本身就是只有一种类别的时候；
情况3）：只经过了一次特征判别就完成树的训练，或者在训练后，经过“后剪枝”操作后得到的决策树；
情况4）：经过完整的训练，且“后剪枝”没有完全剪完，成为情况3，大部分都是属于情况4.

其学习过程分成三个部分：判别特征的选取，树的生成，减枝。
判别特征的选取：即决策树的根节点和内部节点所表示的含义。这里通常有三种选取方式：ID3的信息增益、C4.5的启发式增益率、CART的基尼系数。
树的生成：即决策树的训练阶段，此时如果引入了“预剪枝”，那么就是边训练边剪枝；
剪枝：分“预剪枝”和“后剪枝”。"预剪枝"就是在树训练阶段，在判断特征选取的时候，预先计算当该判断节点生成前与生成后，整棵树的泛化能力是否有提升，如果有，该判断节点会生成。如果没有，当前节点就是叶子节点；“后剪枝”就是在树训练完成之后，对整棵树自底向上的进行剪枝，判别标准也是剪枝前后，整棵树的泛化能力是否有提升。

2 - 判别特征的选取规则

决策树发展中三大算法：ID3(1986)、C4.5(1993)、CART(1984)。首先他们在判别特征的选取规则上就有不同，不过也有相似之处。判别特征的选取，也就是根节点或者当前内部节点的生成，主要就是希望从根节点到当前节点这条路径选取的样本能够尽可能的相似，如希望能够正确把类别为1的样本，且相似的样本能够分到一起，通常也叫做纯度。
为了使得树的生长更有意义，每个分支必须产生比父节点子集更“类均匀”的子集。也就是每个子节点表示的样本集合都更好的属于特定的类，例如，一个四类问题，假设子集\(X_t\)中的向量等概率的在类中分布。对节点进行划分，使得属于类\(w^1\)和\(w^2\)的点构成一个子集，而类\(w^3\)和\(w^4\)的点构成另一个子集，那么新子集与原子集\(X_t\)相比来说更均匀，或者说更"纯"。所以目的是定义一种量度标准，用于量化节点的不纯度，并将节点分支，从而使得子节点的不纯度比父节点的不纯度减少。常见的节点不纯度就是信息熵。这来源于香农信息论。不难证明，如果所有的概率都相等，那么信息熵值最大，如果所有类都属于同一类，那么信息熵的计算值为0。所以决策树的生成，可以看成是不断地减少数据集不纯度的过程。

2.1 - 信息增益：

首先，是引入信息熵的概念，且\(Ent(D)\)的值越小，则其纯度越高：

\[Ent(D) = -\sum_{k=1}^{|y|} p_klog_2p_k\tag{2.1} \]

\(|y|\)表示样本的总类，如果\(|y|=2\)那么这就是个二分类数据集；\(p_k\)表示第\(k\)类样本在所有样本中占的比例为。且\(Ent(D)\)表示的就是所要划分的节点的信息熵，而接下来就是需要确定以哪个特征作为下一个判别特征从而划分该节点。假定当前可选的特征集合为\(F\),其第\(i\)个特征为\(F_i\)。假定当前考虑的特征\(F_i\)一共有\(V\)种情况，那么如果以当前特征作为判别特征，则会从当前需要划分的节点上生成\(V\)条连接，那么这\(V\)条连接中，第\(v\)个连接上的样本个数，假定为\(|D^v|\)，那么第\(v\)个连接上的权重概率即为\(\frac{|D^v|}{|D|}\)，可以看出，权重越大，则当前连接划分的样本就越多。从而，计算出如果使用当前特征作为判别特征，那么其信息增益为：

\[Gain(D,F_i) = Ent(D)-\sum_{v=1}^V\frac{|D^v|}{|D|}Ent(D^v) \tag{2.2} \]

通常来说，信息增益越大，意味着使用判别特征\(F_i\)进行划分所获得的“纯度”越大。所以选择信息增益最大的。

2.1.1 - 离散特征

这里拿周老师西瓜书上的例子来说明（离散特征）：

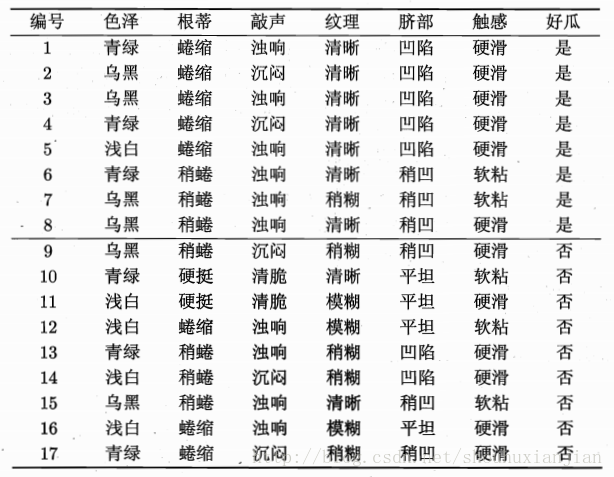
图2.1 周老师西瓜书上表4.1
1 - 根节点的确定
以图2.1举例。因为是2个类别，即\(|y|=2\)，且该训练集包含了 17个样本。其中正例\(p_1=\frac{8}{17}\)，反例\(p_2=\frac{9}{17}\)。则根节点的信息熵为：

\[Ent(D) = -\sum_{k=1}^2p_klog_2p_k=-(\frac{8}{17}log_2\frac{8}{17}+\frac{9}{17}log_2\frac{9}{17})=0.998\tag{2.3} \]

且当前判别特征集合为{色泽、根蒂、敲声、纹理、脐部、触感}。假设先考虑"色泽"这个特征，它是离散值，只有三个取值:{青绿，乌黑，浅白}，即当前\(V=3\)。且可以得到三个数据集的子集:
\(D^1\)(色泽=青绿)={1，4，6，10，13，17}，且只有2种样本类别，则\(p_1 = \frac{3}{6}\),\(p_2=\frac{3}{6}\)；
\(D^2\)(色泽=乌黑)={2，3，7，8，9，15},则\(p_1=\frac{4}{6}\),\(p_2=\frac{2}{6}\)；
\(D^3\)(色泽=浅白)={5，11，12，14，16},则\(p_1 = \frac{1}{5}\),\(p_2=\frac{4}{5}\)。
以"色泽"作为当前结点（目前是根节点）的判别特征的话，对应的三个信息熵为：
\(Ent(D^1) = 1.000\),\(Ent(D^2)=0.918\),\(Ent(D^3)=0.722\)其信息增益为：

\[Gain(D,色泽)= Ent(D)-\sum_{v=1}^3\frac{|D^v|}{|D|}Ent(D^v)=0.109 \tag{2.4} \]

对应的其他几个特征的信息增益为：
\(Gain(D,根蒂)=0.143\)，\(Gain(D,敲声)=0.141\)，\(Gain(D,纹理)=0.381\)，\(Gain(D,脐部)=0.289\)，\(Gain(D,触感)=0.006\)
因为"纹理"的信息增益最大，所以第一个判别特征选择为“纹理”:

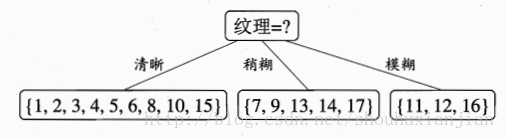
图2.2 第一层(根节点)的划分结果
ps:因为是离散性质的特征，所以对于第二层来说，就可以直接将使用过的特征剔除当前层的候选判别特征集合了，因为是基于父节点的先验概率基础上做的进一步划分，即第二层只要基于{色泽、根蒂、敲声、脐部、触感}来考虑怎么划分，而如果是连续型的特征，就可以不做剔除这一步,只是缩小范围，后面会说到。
2 - 第二层节点的确定
基于图2.2基础，我们现在需要划分第二层的清晰节点，该节点上有数据集\(D^1 = \{1,2,3,4,5,6,8,10,15\}\)，因为这是离散特征，且传到该节点就是基于特征（纹理）先验基础上的，所以当前的候选特征集合 \(F=\{色泽、根蒂、敲声、脐部、触感\}\)。
1）先计算节点的信息熵：$Gain(D^1) =-(\frac{7}{9}log_2\frac{7}{9}+\frac{2}{9}log_2\frac{2}{9})=0.764 \( 2)\)Gain(D^1,色泽) = 0.764-(\frac{4}{9}[-(\frac{3}{4}log_2\frac{3}{4}+\frac{1}{4}log_2\frac{1}{4})]+\frac{4}{9}[-(\frac{3}{4}log_2\frac{3}{4}+\frac{1}{4}log_2\frac{1}{4})]+\frac{1}{9}(\frac{1}{1}log_2\frac{1}{1}))=0.043\( 同理： \)Gain(D^1,根蒂)=0.458$; \(Gain(D^1,敲声)=0.331\); \(Gain(D^1,脐部)=0.458\); \(Gain(D^1,触感)=0.458\);
因为有三个相同的最大值，所以任意取一个就行，这里假设取"根蒂"，从而得到新的三个样本集：
\(D^1 = \{1,2,3,4,5\}\); \(D^2=\{6,8,15\}\); \(D^3 = \{10\}\)
因为对于此时的\(D^1\)都属于同一个类别，所以无需再划分，而\(D^3\)也是同理。对于\(D^2\)因为包含了3个样本，2个正类，1个负类，且当前没有引入"预剪枝"，所以树生成阶段，就会一直生成到最后。通过迭代，最后生成图2.3。

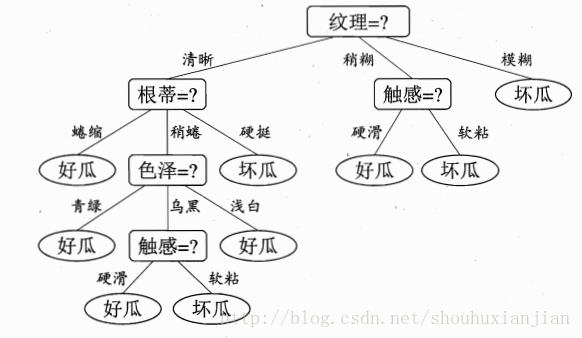
图2.3 西瓜书上图4.4

2.1.2 - 连续特征

我们获取的“样本x特征”矩阵，其值呈现的都是确定值。所谓离散特征，就是当前特征的取值有限，且经常重复出现；而连续值，就是具有多个取值，基本上都看不到重复那种，可以认为是连续的。如2.1.1是处理当特征为离散时候的情况，而很多时候，我们得到的特征是连续值。以西瓜书的表4.3作为例子。

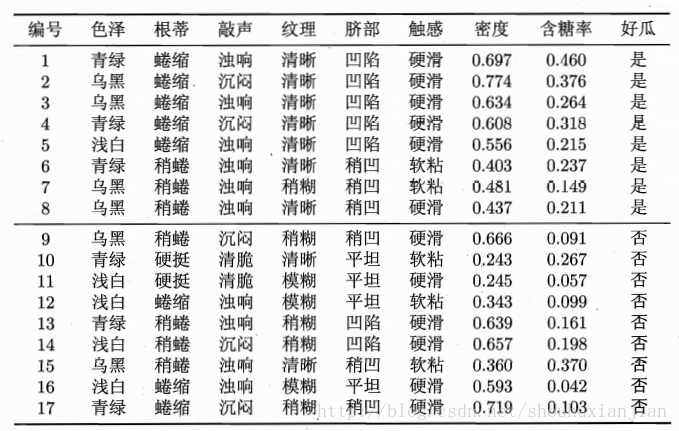
图2.4 西瓜书表4.3
这里相对于图2.1 增加了2个特征，密度和含糖率，这2个都是连续值。而为了应对这种情况时，可以通过m分法，将其分成m份，且以相邻的两个特征点的平均值作为划分点，从而得到m个所谓的离散区域，此时\(m \leq n\),n为训练集样本个数。如候选特征集合中\(F_i=\{f_1,f_2,f_3,...,f_n\}\)（这n个特征值从小到大排序的）。对于划分点\(t\)来说，其值为\(\frac{1}{2}(f_{t-1}+f_{t+1})\),所以t一共有\(n-1\)个可能。不过如此区分，带来的计算量也是巨大的。C4.5中采用的是\(m =2\)的情况。从而当前特征其实可以划分成2个离散区域。且通过如下形式选取最优的那个划分点：

\[\begin{eqnarray} Gain(D,F_i) &=& max_{t}Gain(D,F_i,t)\\ &=& max_{t}Ent(D)-\sum_{\lambda \in \{-,+\} }\frac{|D^\lambda|}{|D|}Ent(D_t^\lambda) \end{eqnarray} \tag{2.5}\]

如图2.4中 密度有16个候选划分点
\(\{0.244, 0.294, 0.351, 0.381, 0.420, 0.459, 0.518, 0.574, 0.600, 0.621, 0.636, 0.648, 0.661, 0.681, 0.708, 0.746\}\)
从而计算得出其最佳划分点为0.381，对应的信息增益为0.262.
\(Gain(D,密度,0.381) = 0.998-(-[\frac{13}{17}(\frac{8}{13}log_2\frac{8}{13}+\frac{5}{13}log_2\frac{5}{13})+\frac{4}{17}(\frac{0}{4}log_2\frac{0}{4}+\frac{4}{4}log_2\frac{4}{4})]) = 0.262\)
同理得，含糖率最佳划分点0.126，信息增益为0.349。从而得到：
\(Gain(D,色泽)=0.109\)；\(Gain(D,根蒂)=0.143\)； \(Gain(D,敲声) =0.141\)；\(Gain(D,纹理)=0.381\)；\(Gain(D,脐部) = 0.289\)；\(Gain(D,触感) = 0.006\)； \(Gain(D,密度) = 0.262\)； \(Gain(D,含糖率)=0.349\)

ps:假如选取了密度为当前的判别特征，则其左边子树是密度小于0.381的样本，右子树是大于0.381的点。因为该特征是连续值，故而不会被剔除下一层的判别特征的候选集合，因为对于小于0.381的样本集合(即左子树)来说，其还是可以从范围\([min,0.381)\)接着进一步选取下一层的最佳划分点，然后将其离散化。

2.2 - 信息增益率

因为2.1的信息增益方法对于当该特征的取值较多时候，会有所偏差，比如一个特征只有2个取值，一个特征却能取3个值，这时候信息增益方法会稍微倾向于选择能取3个值得特征作为判别特征。为了解决这种特征取值个数带来的问题，C4.5选择使用信息增益率的方式作为判别特征的选取规则。
增益率公式为：

\[Gain\_ratio(D,F_i) = \frac{Gain(D,F_i)}{IV(F_i)} \tag{2.6} \]

这里\(IV(F_i)\)就是该特征的“固有值”，其可取值的数量越多(\(V\)越大)，则\(IV(F_i)\)通常越大。其计算公式为：

\[IV(F_i) = -\sum_{v=1}^V\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|} \tag{2.7} \]

如图2.1所示的数据集:

\[IV(触感,V=2) =-(\frac{5}{17}log_2\frac{5}{17}+\frac{12}{17}log_2\frac{12}{17}) = 0.874 \]

\[IV(色泽,V=3) = 1.580 \]

\[IV(编号,V=17) = 4.088 \]

可以发现，计算公式和计算信息增益是一样的，只是信息增益是基于样本标签，而这里是计算该特征的几个不同的取值。增益率规则对可取值数目较少有偏好，所以C4.5采用了启发式增益率，即先从当前候选特征集合中找到信息增益高于平均水平的特征，组成新候选特征集合，然后再计算这个新候选特征集合中增益率高的那个。相当于设定一个自适应阈值，将大于该阈值的特征留下，然后取留下特征中增益率高的特征。

2.3 - 基尼系数

在CART算法中，采取的是基尼系数的方式来衡量判别特征。
数据集D的纯度可用基尼值来度量：

\[\begin{eqnarray}Gini(D) &=& \sum_{k=1}^{|y|} \sum_{k^` \neq k}p_kp_{k^`}\\ &=& 1 - \sum_{k=1}^{|y|}p_k^2 \end{eqnarray}\]

直观来说，\(Gini(D)\)反映了从数据集D中随机抽取两个样本，其类别标记不一致的概率，所以同样也是，其值越小，数据集D的纯度越高。
候选判别特征\(F_i\)的基尼指数定义为：

\[Gini\_index(D,F_i) = \sum_{v=1}^V\frac{|D^v|}{|D|}Gini(D^v) \]

所以在候选特征集合中选择使得划分后基尼指数最小的熟悉作为最优划分属性，即\(argmin_{F_i\in F}Gini\_index(D,F_i)\)

2017/03/17 第一次修改！
参考资料：
[1] 模式识别 第4版.(希腊)西奥多里蒂斯
[2] 周志华，机器学习
[3]