Clustering[Spectral Clustering]
0. 背景
谱聚类在2007年前后十分流行,因为它可以快速的通过标准的线性代数库来实现,且十分优于传统的聚类算法,如k-mean等。
至于在任何介绍谱聚类的算法原理上,随便翻开一个博客,都会有较为详细的介绍,如这里。当然这些都来自《A Tutorial on Spectral Clustering》一文。为了上下文一致性和便于理解,我就直接截图别人基于这篇论文中翻译好的部分(偷懒):
- 1 - 无向权重图:谱聚类是基于图论结构,也是数据结构的毗邻矩阵来实现的,即将所有的点的看成是一个相互连接的图(graph);
上图中\(|A|\)即为聚类后的一个类别的数据点集合;- 2 - 相似矩阵:通过定义相似函数,计算不同点之间的相似性,将其作为两点之间连线上的权重值。相距越近,则权重越大,越远则权重值越小;
其中第三种全连接方法的高斯方差决定了近邻的范围是多大;- 3 - 最后当然就是想着怎么把图给切割开,fisher准则就是聚类的目的为:类内间距最小,类间间距最大。从而期望于切割整个图之后,子图之间连线的权重之和最小;
1. 谱聚类
如上述第三点所述,当我们构建了图,定义了相似函数,得到了毗邻矩阵和度矩阵之后。一步到位的想法就是怎么切割,不过显然还是需要其他知识介入。
谱聚类可以通过线性代数关于这两个矩阵的特征值和特征向量来考虑,而通过这两个矩阵组合的叫做图拉普拉斯矩阵“graph laplacian matrices”。有个领域叫做“spectral graph theory”,研究了不少这些矩阵的特性,这么说是图拉普拉斯矩阵不止一个形式。
1.1 未归一化的图拉普拉斯矩阵
我们总假设\(G\)是一个无向的,具有权重矩阵\(W\)的权重图,其中\(w_{ij}=w_{ji}>0\)。当使用这个矩阵的特征向量时,不需要进行归一化,且特征值以升序排序。前k个特征向量,表示的就是前k个最小特征值对应的特征向量。
未归一化的拉普拉斯矩阵的特性

上述中,涉及到几个线性代数的知识:
- 一个实数对称矩阵的所有特征值都是实数(来自《introduction to linear algebra》chapter 6.4)
- 证明一个矩阵是半正定的方式如下(来自《introduction to linear algebra》chapter 6.5)
值得注意的是,上述的拉普拉斯矩阵是未归一化的,该矩阵不依赖于毗邻矩阵\(W\)的对角元素,且所有非对角位置上与W一致的邻接矩阵可以得到相同的非归一化的拉普拉斯矩阵,即图中所有的自连接的点不影响对应的图拉普拉斯,即点之间的关系才影响。
非归一化的图拉普拉斯矩阵和他的特征值和特征向量可以用来描述图的许多特性,下面的参考文献中Mohar等人的工作有较为详细的研究。
联通子图的个数
假设\(G\)是一个无向图,其中的权重都是非负的。那么特征值0的自由度个数(原文叫multiplicity,重数)等于联通子图的个数,即假设有k个重数,那么就有\(A_1,A_2,...A_k\)个子图,且特征值0的特征空间可以通过指示向量(基向量)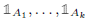 表示。
表示。
证明:
- k=1:即整个图被归为1类,假设\(f\)是特征值0的特征向量,那么:
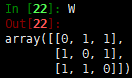
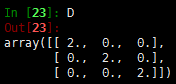
因为\(w_{ij}\)是非负的,所以和为0的时候即\(w_{ij}(f_i-f_j)^2\)等于0,那么假设两个点是相连的,即\(w_{ij}>0\),那么\(f_i=f_j\)。这样的话,可以发现对于所有可以通过某个路径进行相连的所有点,在\(f\)中的值都是相同的。那么如果只有一个类别,那么就只有一个向量。我们举个例子,假设有一个图,其中3个节点,两两相连,权重值都为1:
![]()
![]()
可以看出,第二个特征值为0(近似),其对应的特征向量为\([-0.57,-0.57,-0.57]=-0.57*[1,1,1]\),而\([1,1,1]\)被称为常量向量- k=其他值。
不失一般性,假设图中的所有的点都是按照其对应的子图类进行有序排列的,在这种情况下,毗邻矩阵\(W\)可以变成一个块矩阵组成的形式,当然对于\(L\)也是一样的:
可以发现每个块\(L_i\)都是一个对应的图拉普拉斯子矩阵,对应着第\(i\)个连通子图。那么依据矩阵的知识,相当于将整个矩阵划分成相同特性的多个子矩阵,其中\(L\)的特征向量就等于第\(L_i\)个特征向量的值加上其他子矩阵维度上为0。且\(L_i\)是一个联通图,那么其就有特征值为0且所有元素为1的特征向量。因此,矩阵\(L\)的子矩阵中特征值为0的个数就等于联通子图的个数。
1.2 归一化的图拉普拉斯矩阵
有2个矩阵被称为归一化的图拉普拉斯。这两个矩阵较为相似:
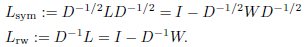
第一个矩阵是一个对称矩阵,第二个和随机游走十分相关。关于归一化图拉普拉斯矩阵的知识,可以参见参考文献中Chung的
\(L_{sym}\)和\(L_{rw}\)的特性
这两个归一化的拉普拉斯矩阵具有以下特性:
- 1 - 对于任何向量\(f\in R^n\),有:
- 2 - 有且仅有\(\lambda\)和\(w=D^{1/2}u\)分别是\(L_{sym}\)的特征值和特征向量时,\(\lambda\)和\(u\)就是是\(L_{rw}\)的特征值和特征向量;
- 3 - 有且仅有\(\lambda\)和\(u\)满足\(Lu=\lambda Du\)时,\(\lambda\)和\(u\)是\(L_{rw}\)的特征值和特征向量
- 4 - 0和常量向量
是\(L_{rw}\)的特征值和特征向量,0和\(D^{1/2}\)
是\(L_{sym}\)的特征值和特征向量
- 5 - \(L_{sym}\)和\(L_{rw}\)都是半正定的,且有n个非零的实值特征值,\(0\leq \lambda_1 \leq \lambda_2 ...\leq \lambda_n\)
联通子图的个数
假设\(G\)是一个无向图,其中权重都是非负的,那么\(L_{rw}\)和\(L_{sym}\)的特征值为0的自由度个数等于图中联通子图的个数,
- 对于\(L_{rw}\),其0特征值对应的特征空间的基向量为这些子图对应的指示向量
;
- 对于\(L_{sym}\),其0特征值的特征空间的基向量为
可以看出,上述就是第4个特性。将未归一化的拉普拉斯的联通子图的个数的推论等效应用到归一化的拉普拉斯矩阵上即可。
2.聚类方法
对于第一种未归一化的拉普拉斯矩阵情况:

上述步骤可以简单归纳为:
- 1 - 选择合适的相似函数,计算相似矩阵
- 2 - 计算度矩阵\(D\),毗邻权重矩阵\(W\),从而建立拉普拉斯矩阵\(L\)
- 3 - 计算拉普拉斯矩阵\(L\)的前k个特征向量,组成矩阵\(n\times k\)
- 4 - 用k-mean算法将上述的特征向量矩阵按行为样本(即\(n\)个样本),列为特征(即k个特征)进行k个类别的聚类。
对于第二种归一化的拉普拉斯矩阵情况,因为有2种矩阵,故而有两种情况:

- 上述图中,该算法使用的是\(L\)的广义特征向量。上述流程作用于\(L_{rw}\),所以称为归一化的谱聚类。

- 上述图中,该算法使用的是\(L_{sym}\),并且添加了一个额外的行归一化,同样也是归一化的谱聚类。
上述三个算法都基本大同小异,除了他们使用的是不同的拉普拉斯矩阵。这三个算法中,最主要的技巧就是将抽象的数据点\(x_i\)的表征转换成\(y_i\in R^k\)。这是因为拉普拉斯矩阵的特性可以让这样的转变十分有用。而且表征的转变增强了数据中的聚类属性,从而可以轻松的在新的表征中进行检测类的聚合。
【待续。。。】
参考文献:
[] 1 - Mohar, B. (1991). The Laplacian spectrum of graphs. In Graph theory, combinatorics, and applications. Vol. 2 (Kalamazoo, MI, 1988) (pp. 871 { 898). New York: Wiley
[] 2 - Mohar, B. (1997). Some applications of Laplace eigenvalues of graphs. In G. Hahn and G. Sabidussi (Eds.), Graph Symmetry: Algebraic Methods and Applications (Vol. NATO ASI Ser. C 497, pp. 225 { 275). Kluwer
[] 3 - Chung, F. (1997). Spectral graph theory (Vol. 92 of the CBMS Regional Conference Series in Mathematics). Conference Board of the Mathematical Sciences, Washington





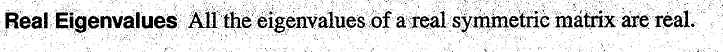
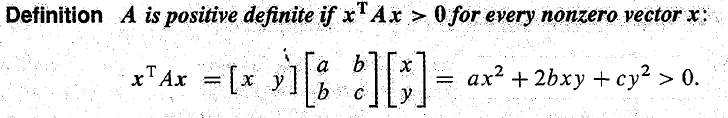
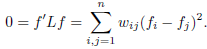



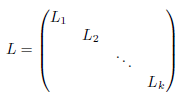
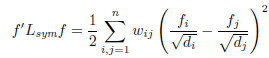
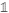 是
是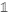 是
是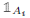 ;
;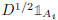

 浙公网安备 33010602011771号
浙公网安备 33010602011771号